
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основная теорема алгебры и её следствия. Теорема Виета
|
|
|
|
Определение. Если 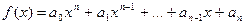 есть некоторый многочлен, а
есть некоторый многочлен, а 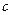 некоторое число, то число
некоторое число, то число 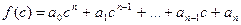 , полученное заменой в выражении для
, полученное заменой в выражении для 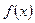 неизвестного число
неизвестного число 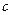 и последующим выполнением всех указанных операций, называется значением многочлена
и последующим выполнением всех указанных операций, называется значением многочлена 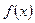 при
при 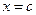 .
.
Если 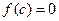 , то
, то 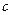 называется корнем многочлена
называется корнем многочлена 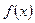 (или уравнения
(или уравнения 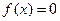 ).
).
Теорема. Остаток от деления многочлена 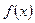 на линейный многочлен
на линейный многочлен 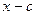 равен значению
равен значению 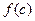 многочлена
многочлена 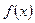 при
при 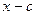 , т.е.
, т.е. 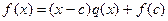 .
.
Теорема Безу. Число 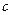 является корнем
является корнем 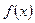

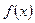 делится на
делится на 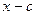 .
.
Метод Горнера - метод деления 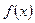 на
на 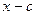 .
.
Если 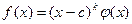 , где
, где  на
на 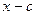 уже не делится, то
уже не делится, то 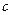 называется
называется 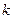 -кратным корнем
-кратным корнем 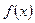 ,
, 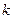 - кратностью корня
- кратностью корня 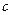 . Если
. Если 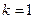 , то говорят, что корень
, то говорят, что корень 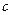 - простой.
- простой.
Всякий многочлен с любыми числовыми коэффициентами, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный.
Теорема. Всякий многочлен 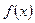 степени
степени 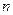 ,
, 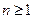 , с любыми числовыми коэффициентами имеет
, с любыми числовыми коэффициентами имеет 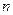 корней, если каждый из корней считать столько раз, какова его кратность.
корней, если каждый из корней считать столько раз, какова его кратность. 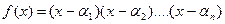
Это разложение единственно с точностью до порядка сомножителей.
Также рассматриваются формулы Виeта.
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 1196; Нарушение авторских прав?; Мы поможем в написании вашей работы!