Лекция 10. Скалярное, векторное и смешанное произведение векторов

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

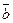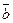Скалярное произведение векторов и будем обозначать символом . Если угол между векторами и равен 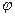, то по определению скалярное произведение этих двух векторов выражается формулой

.

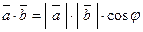Из этой формулы следует, что . Число называется скалярным квадратом вектора и обозначается через 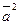. Таким образом, .

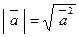Теорема. Два вектора ортогональны (перпендикулярны) тогда и только тогда, когда их скалярное произведение равно нулю.

Теорема. Два вектора и 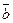составляют острый (тупой) угол тогда и только тогда, когда их скалярное произведение положительно (отрицательно).

Свойства скалярного произведения.

1.

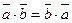
2.

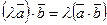
3.

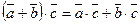
4. , если - ненулевой вектор, и 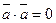, если - нулевой вектор.

Теорема. Скалярное произведение векторов 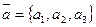и 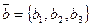, заданных в ортонормированном базисе, выражается формулой

.

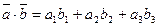Доказательство. Пусть 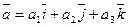и . Тогда используя свойства скалярного произведения, будем иметь

.

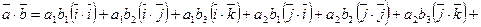
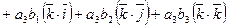Так как базис 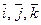ортонормированный, то 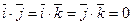и . Следовательно, .

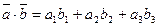Следствие1. Векторы 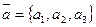и 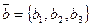, заданные в ортонормированном базисе, перпендикулярны тогда и только тогда, когда

.

Следствие 2. Угол между векторам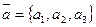и и 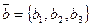определяется по формуле

.

Выясним геометрический смысл координат вектора в ортонормированном базисе. Пусть в ортонормированном базисе 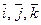задан ненулевой вектор 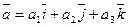. Умножим обе части скалярно на 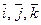. Получим, что . Если ввести обозначения 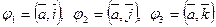, то будем иметь

.

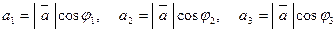Числа называются направляющими косинусами вектора в базисе 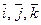. Отметим, что

.

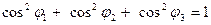Три вектора называются упорядоченной тройкой, если указано, какой из этих векторов является первым, какой – вторым, и какой –третьим.

Пусть дана тройка некомпланарных векторов 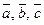. Будем говорить, что эти векторы образуют правую тройку, если из конца вектора 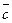кратчайший поворот от вектора к вектору 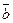виден в направлении, противоположном направлению движения часовой стрелки. Иначе, будем говорить, что векторы 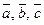образуют левую тройку.

Векторным произведением вектора на вектор 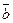называется вектор 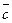, обозначаемый символом 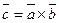и удовлетворяющий условиям:

1.

2.

3. 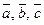– правая тройка.

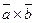
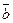
Теорема. Два вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулю.

Утверждение 2.5. Длина (модуль) векторного произведения равна площади параллелограмма, построенного на векторах и .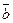

Свойства векторного произведения.

1.

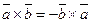
2.

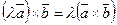
3.

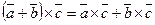
4. для любого вектора .

Теорема. Векторное произведение двух векторов 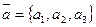и 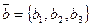, заданных своими декартовыми прямоугольными координатами, вычисляется по формуле

.

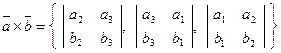Рассмотрим упорядоченную тройку векторов 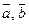и .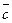

Смешанным произведением 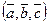векторов 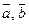и 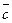называется число, вычисляемое по формуле .

Теорема. Смешанное произведение 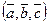равно объему параллелепипеда, построенного на приведенных к общему началу векторах 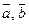и 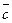, взятому со знаком плюс, если тройка 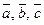правая, и со знаком минус, если тройка 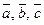левая. Если же векторы 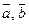и 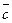компланарны, то 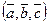равно нулю.

Теорема. Три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.

Теорема. Смешанное произведение трех векторов 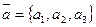, 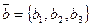и , заданных своими декартовыми прямоугольными координатами, вычисляется по формуле

.

Доказательство. Выше было показано, что 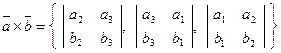. Поскольку , то, используя формулу скалярного произведения векторов, будем иметь

.

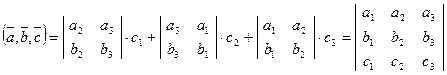Свойства смешанного произведения.

1.

2.

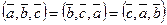
3. , ,

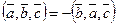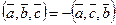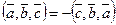
4.

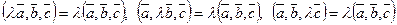
5. ,

Дата добавления: 2014-12-24