Парабола. Касательные к эллипсу, гиперболе и параболе

.

Откуда 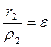. Аналогично и для второго фокуса.

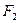Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух данных точек и , называемых фокусами гиперболы, есть величина постоянная , меньшая, чем расстояние между фокусами .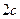

Для вывода канонического уравнения гиперболы систему координат 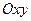выберем так же, как и для эллипса. Тогда будем иметь 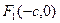, . Согласно определению гиперболы: 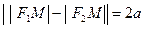. Отсюда, переходя к координатам, после несложных преобразований, получим каноническое уравнение гиперболы:

, где .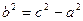

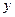
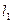
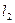
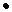
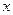
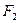
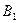
Свойства гиперболы.

1. Координатные оси являются осями симметрии, а начало координат – центром симметрии гиперболы.

2. Гипербола пересекает ось абсцисс в точках 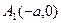, 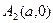и не пересекает ось ординат.

3. Координаты 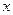и 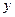любой точки гиперболы могут изменяться в пределах , .

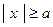4. При возрастании абсциссы 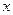в промежутке 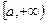(в первой координатной четверти) ордината возрастает от 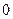до .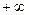

Отрезок 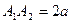называется действительной осью, а 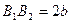- мнимой осью гиперболы.

Число 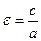называется эксцентриситетом гиперболы. Очевидно, что для гиперболы 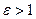. Так же, как и у эллипса, эксцентриситет гиперболы характеризует ее форму – степень сжатия ветвей гиперболы к оси абсцисс.

Прямые 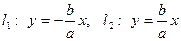называются асимптотами гиперболы. Ветви гиперболы, уходя в бесконечность, неограниченно приближаются к соответствующим асимптотам.

Прямые 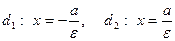называются директрисами гиперболы.

Так же как и для эллипса справедливо

Теорема. Отношение расстояния от любой точки гиперболы до фокуса к расстоянию до соответствующей директрисы есть величина постоянная, равная эксцентриситету.

Гипербола, у которой , называется равносторонней.

Гиперболы с уравнениями и называются сопряженными.

Параболой называется множество точек плоскости, расстояние от каждой из которых до данной точки , называемой фокусом, равно расстоянию до данной прямой , не проходящей через точку . Прямая называется директрисой параболы.

Расстояние 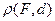от фокуса до директрисы обозначается буквой и называется параметром параболы.

Систему координат выберем следующим образом. Ось абсцисс 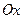проведем через фокус перпендикулярно к директрисе в направлении от к , а ось ординат 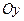- перпендикулярно к оси 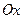через середину отрезка, соединяющего фокус с директрисой. При выбранной системе координат уравнение директрисы будет иметь вид 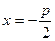, а фокус .

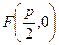Пусть 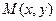- произвольная точка параболы. Тогда по определению 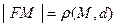. Переходя к координатам, будем иметь

.

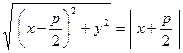Возводя уравнение в квадрат, получаем каноническое уравнение параболы

.

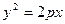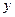
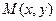
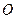
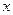
Свойства параболы.

1. Абсцисса любой точки параболы больше нуля.

2. Парабола проходит через начало координат.

3. Парабола симметрична относительно оси абсцисс.

4. При неограниченном возрастании абсциссы 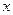ордината 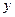возрастает по абсолютной величине.

Дата добавления: 2014-12-24