Лекция 13. Плоскость в пространстве. Различные виды уравнения плоскости. Расстояние от точки до плоскости. Взаимное расположение двух плоскостей

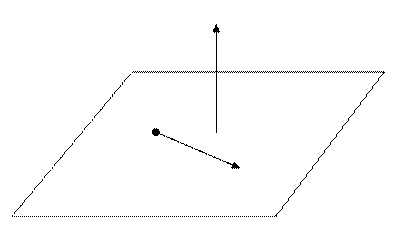
Пусть в пространстве в прямоугольной системе координат 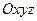дана плоскость 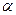, проходящая через точку и перпендикулярная вектору . Этот вектор будем называть вектором нормали плоскости .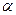

Очевидно, что существует единственная плоскость, проходящая через данную точку 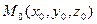перпендикулярно вектору . Составим уравнение этой плоскости.

Пусть - произвольная точка плоскости .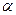

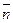
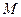
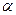
Нетрудно понять, что вектор принадлежит плоскости 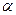тогда и только тогда, когда 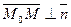. Это означает, что 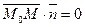. Или в координатах

.

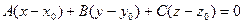Откуда

.

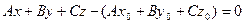Введя обозначение , окончательно запишем

.

Это уравнение называется общим уравнением плоскости. А уравнение

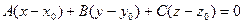
называется уравнением плоскости, проходящей через точку 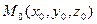перпендикулярно вектору .

Уравнение плоскости, проходящей через три точки 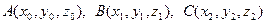, не принадлежащие одной прямой, имеет вид

.

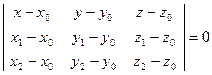Пусть плоскость отсекает на координатных осях отрезки соответственно . Тогда 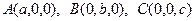- точки пересечения данной плоскости с осями координат. Отсюда, согласно вышеприведенному уравнению, получим уравнение

.

Это уравнение называется уравнением плоскости в отрезках.

Пусть плоскость 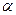проходит через данную точку 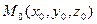и имеет направляющее подпространство с базисом . Точка принадлежит плоскости 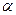тогда и только тогда, когда векторы 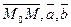компланарны. Это условие можно записать в виде .

В координатах имеем

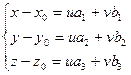, где 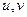- параметры.

Эти уравнения называются параметрическими уравнениями плоскости.

Теперь запишем нормальное уравнение плоскости. Расстояние от начала координат до плоскости обозначим буквой . За нормальный вектор плоскости примем единичный вектор 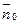с началом, совпадающим с началом координат.

Если нормальный вектор образует с осями координат соответственно углы 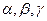, то очевидно, что координатами этого вектора будут косинусы его направляющих векторов: 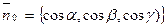. Если 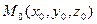- некоторая фиксированная точка плоскости, а - произвольная ее точка, то уравнение этой плоскости, проходящей через точку и имеющей нормальный вектор 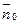, запишется в виде

.

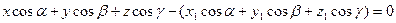Нетрудно понять, что . Тогда последнее уравнение примет вид

.

Это уравнение называется нормальным уравнением плоскости.

Для перехода от общего уравнения плоскости к нормальному надо общее уравнение умножить на так называемый нормирующий множитель

.

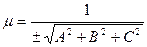Знак выбирается противоположным свободному члену общего уравнения плоскости.

Расстояние от точки 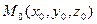до плоскости вычисляется по формуле

.

Если плоскость задана нормальным уравнением, то расстояние будет вычисляться по следующей формуле

.

Пусть даны две плоскости:

, .

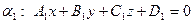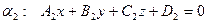За угол между этими плоскостями примем угол между их нормальными векторами: . Тогда

.

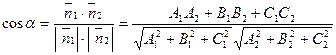Теорема. Пусть даны плоскост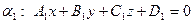и и 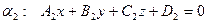. Тогда

1.

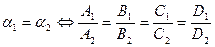
2.

3.

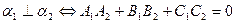
4. 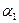и пересекаются, если нарушено одно из условий в соотношениях .

Дата добавления: 2014-12-24