Лекция 9. Векторы. Базис векторного пространства

Абстрагируясь от конкретных свойств, встречающихся в природе физических векторных величин, мы приходим к понятию геометрического вектора, или просто вектора.

Геометрическим вектором (или просто вектором) будем называть направленный отрезок.

Вектор будем обозначать либо символом 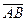, где точк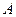и и обозначают соответственно начало и конец данного направленного отрезка (вектора), либо одной латинской буквой, например или .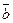

Начало вектора называют точкой его приложения. Длиной вектора 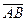называют длину отрезка 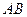и обозначают символом .

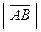Вектор называется нулевым, если начало и конец его совпадают. Нулевой вектор не имеет определенного направления и имеет длину, равную нулю. Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.

Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление. Мы не будем различать два равных вектора, имеющих разные точки приложения и получающиеся один из другого параллельным переносом. В соответствии с этим векторы, изучаемые в геометрии, называют свободными (они определены с точностью до точки приложения).

Векторы называются компланарными, если они лежат либо в одной плоскости, либо в параллельных плоскостях.

Линейными операциями над векторами называют операцию сложения векторов и операцию умножения векторов на вещественные числа.

Суммой 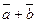двух векторов и 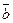называется вектор, идущий из начала вектора в конец вектора 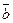при условии, что вектор 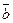приложен к концу вектора

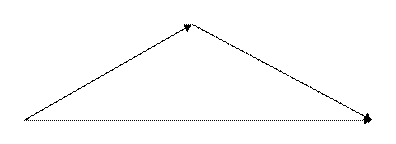
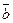
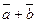
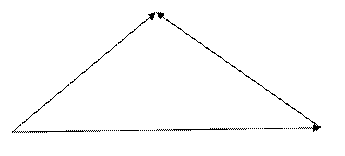
Это правило называется правилом треугольника.

Разностью 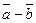вектора и вектора 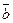называется такой вектор, который в сумме с вектором 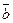дает вектор .

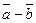
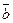
Произведением вектора на вещественное число 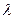называется вектор 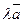, который определяется следующим образом:

;

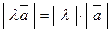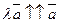, есл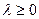и и 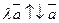, если .

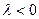В случае, когда 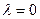или 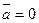, произведение 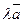представляет собой нулевой вектор, направление которого неопределенно.

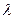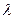Геометрический смысл операции умножения вектора на число можно выразить так: при умножении вектора на число вектор «растягивается» в «раз».

Свойства линейных операций.

1. 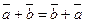(коммутативность);

2. 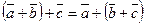(ассоциативность);

3. существует нулевой вектор 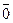такой, что 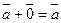для любого вектора (особая роль нулевого вектора);

4. для каждого вектора существует противоположный ему вектор 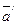такой, что ;

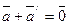5. ;

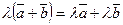6. ;

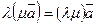7. ;

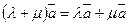8. .

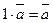Эти свойства имеют фундаментальное значение, ибо они позволяют производить выкладки в векторной алгебре по тем правилам, по которым производятся аналогичные выкладки в обычной алгебре.

Теорема. Если векторы и 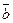коллинеарны и 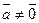, то существует единственное число 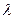такое, что .

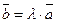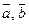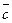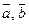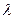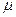Теорема. Если векторы и компланарны, а векторы не коллинеарны, то существуют единственные числа и такие, что .

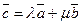Линейной комбинацией векторов 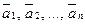называется сумма произведений этих векторов на произвольные вещественные числа, т.е. выражение вида 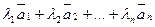, где 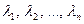- какие угодно вещественные числа.

Система векторов 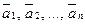называется линейно зависимой, если существуют числа 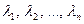, среди которых хотя бы одно отлично от нуля, и такие, что

.

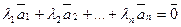Если же последнее равенство выполняется только при 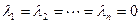, то система векторов 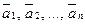называется линейно независимой.

Теорема. Система векторов 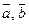линейно зависима тогда и только тогда, когда эти векторы коллинеарны.

Теорема. Система векторов 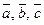линейно зависима тогда и только тогда, когда эти векторы компланарны.

Эти два утверждения раскрывают геометрический смысл линейной зависимости векторов.

Базисом пространства называется такая система векторов, которая задана в определенном порядке и удовлетворяет условиям:

a) система векторов линейно независима;

b) любой вектор пространства является линейной комбинацией данной системы векторов.

Число векторов базиса называется размерностью пространства.

Теорема. Любая тройка некомпланарных векторов 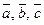образует базис в пространстве. Любая пара лежащих в данной плоскости неколлинеарных векторов 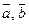образуют базис на этой плоскости.

Теорема. Если векторы 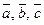не компланарны, то для любого вектора 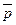существуют единственная тройка чисел числа 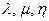такая, что

.

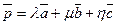Пусть 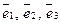- данный базис. Тогда для любого вектора имеет место равенство

.

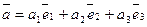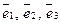Будем говорить, что вектор разложен по базису . Коэффициенты 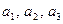в этом разложении называются координатами вектора в данном базисе.

Теорема. При сложении (вычитании) векторов их соответствующие координаты складываются (вычитаются). При умножении вектора на число все его координаты умножаются на это число.

Теорема. Векторы 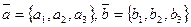коллинеарны тогда и только тогда, когда .

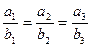При решении задач метрического характера, то есть задач, связанных с вычислением длин отрезков (векторов) или величин углов, удобнее рассматривать ортонормированные базисы.

Базис 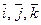называется ортонормированным, если его векторы единичной длины и попарно перпендикулярны.

Теорема. Длина вектора 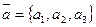, заданного в ортонормированном базисе 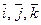, вычисляется по формуле

.

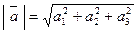Рассмотрим системы координат. На плоскости прямоугольную декартову систему координат 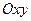образует упорядоченная пара взаимно перпендикулярных осей. Первая ось с единичным вектором 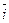называется осью абсцисс 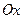, вторая ось с единичным вектором 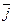- осью ординат 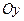, точка пересечения осей 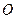называется началом системы координат. Векторы 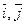образуют базис, а их направления определяют положительные направления осе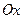й и 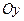соответственно.

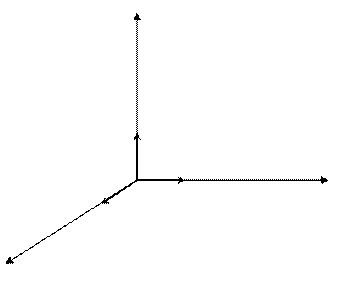
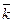
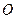
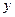
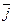
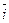
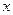
В пространстве прямоугольную декартову систему координат образует упорядоченная тройка взаимно перпендикулярных осей, пересекающихся в общей точке 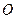, называемой началом системы координат. К осям 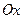с единичным вектором 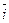и 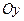с единичным вектором 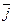прибавляется ось аппликат 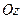с единичным вектором 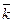. Векторы 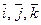образуют ортонормированный базис. Координаты вектора в ортонормированном базисе 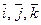будем называть прямоугольными декартовыми координатами.

Дата добавления: 2014-12-24