Общее свойство минимально-фазовых устойчивых звеньев

Общим показателем свойств звена является принадлежность нулей передаточной функции к левой полуплоскости. Представляя передаточную функцию в форме (1.6), комплексный коэффициент передачи можно выразить как

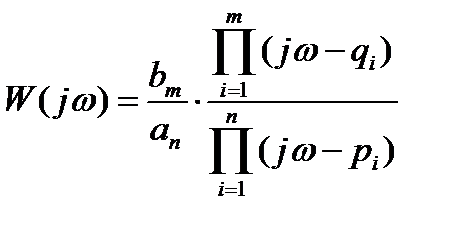. (1.27)

Рассмотрим сомножитель числителя jω-q_i. Эта разность представляет собой вектор, начало которого лежит в точке q_i, а конец на мнимой оси в точке jω. Фаза этого вектора характеризует поворот его относительно вещественной оси против часовой стрелки.

На рисунке 1.10 построены два таких вектора для различных положений точки q_i, обозначенных q_i^' и q_i^''. Из построения видно, что при одном и том же значении модуля комплекса jω-q_i его фаза φ меньше в том случае, когда q_i лежит в левой полуплоскости. Поэтому звенья, все нули передаточной функции лежат в левой полуплоскости (Re q_i<0), называются минимально-фазовыми. Звенья, передаточные функции которых имеют хотя бы один нуль, лежащий в правой полуплоскости (Re q_i.>0), называются неминимально-фазовыми.

Рисунок 1.10 – Минимально- и неминимально-фазовые звенья

Для минимально-фазовых устойчивых звеньев между амплитудно-частотной и фазочастотной характеристиками существует однозначная зависимость и, следовательно, амплитудно-частотная характеристика однозначно определяет передаточную функцию системы.

Итак, если известна амплитудно-частотная характеристика звена и известно, что звено устойчивое и минимально-фазовое, то этого достаточно для того, чтобы найти все его частотные характеристики и, следовательно, полностью охарактеризовать поведение системы при любых сигналах, поступающих на вход.

Для минимально-фазовой системы определение приближённого значения фазы φ_i(ω_i) можно проводить непосредственно по среднему наклону ЛАЧХ в частоте ω_i без построения ЛФЧХ. При этом

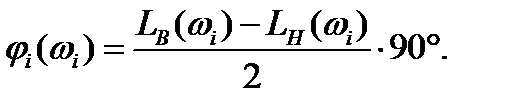(1.28)

Рисунок 1.11 – Определение фазы системы по амплитуде

При этом L_В(ω_i) и L_Н(ω_i) значения ЛАЧХ при частотах, отстоящих от ω_i на одну декаду в сторону увеличения и уменьшения частот соответственно.

Дата добавления: 2014-12-25