Понятие о передаточной функции

Динамика систем регулирования

Под динамикой регулирования понимают исследования с целью решения двух задач:

1. Задача анализа САУ – изучения законов изменения регулируемых величин под воздействием различных возмущений при различных сочетаниях параметров САУ.

2. Задача синтеза САУ – определения структуры и параметров САУ, обеспечивающих заранее заданное качество переходных процессов.

Исходными данными для исследования динамики САУ являются дифференциальные уравнения и структурные схемы, составленные для отдельных элементов САУ на основе тех физических законов, которые определяют процессы в этих элементах. Совокупность дифференциальных или интегрально-дифференциальных уравнений всех элементов системы образует математическое описание САУ в динамике.

В общем случае уравнение, описывающее поведение САУ, является нелинейным. Однако, если поведение САУ в динамике рассматривается при относительно малых по величине отклонениях переменных, то возможно осуществлять линеаризацию дифференциальных уравнений. Такая линеаризация сводится к линеаризации имеющих место нелинейной статической характеристики и нелинейных функций нескольких переменных (двух).

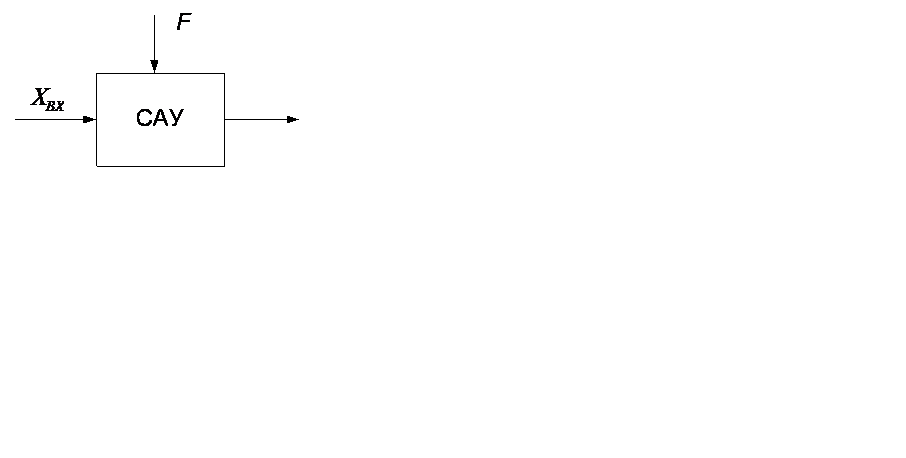
Если решать систему линеаризации дифференциальных уравнений, составленных для каждого элемента САУ относительно какой-либо одной регулируемой величины х(t)=х_ВЫХ(t) по отношению к отклонению

Рисунок 1.1 – Систем АУ х(t)=х_ВХ(t) и к возмущающему воздействию

f (t), то в результате получим дифференциальные уравнения с постоянными коэффициентами следующего вида:

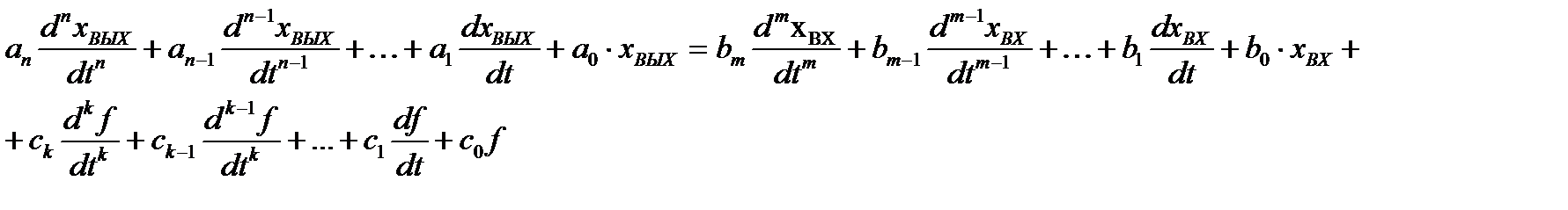, (1.1)

где 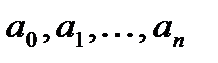; ; 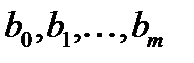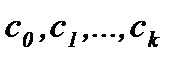- постоянные коэффициенты.

Уравнение (1.1) носит название общего дифференциального уравнения САУ или уравнения движения САУ.

Применяя к уравнению (1.1) при нулевых начальных условиях преобразование Лапласа, запишем это уравнение в операторной форме:

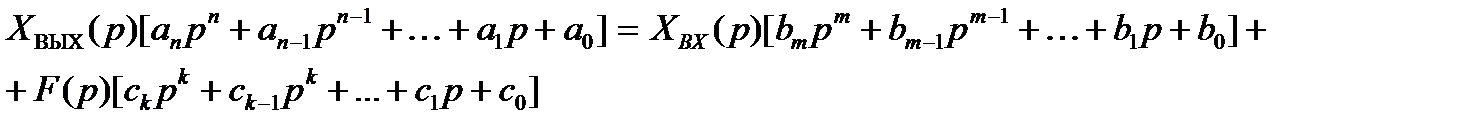, (1.2)

где X_ВЫХ(p); Х_ВХ(p) и F(p) – изображения соответственно функций x_ВЫХ(t); х_ВХ(t) и f(t).

Передаточной функцией САУ по задающему воздействию (рисунок 1.2,а) называется отношение операторного изображения выходной величины САУ к операторному изображению входной величины САУ при нулевых начальных условиях, т.е.:

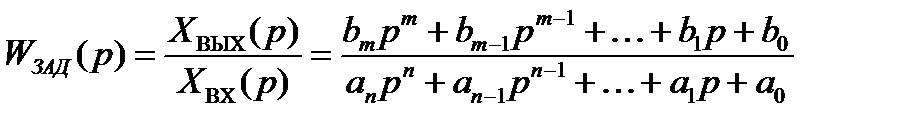. (1.3)

Соответственно, передаточной функцией САУ по возмущающему воздействию (рисунок 1.2,б) называют отношение операторного изображения выходной величины к операторному изображению возмущающего воздействия при нулевых начальных условиях

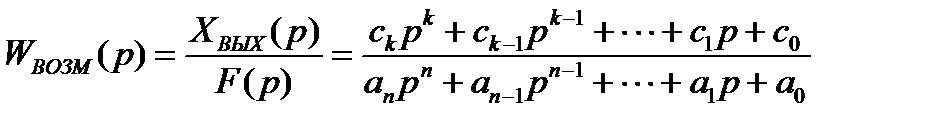. (1.4)

а) б)

Рисунок 1.2 – Передаточные функции

Т.к. при записи уравнений линейной САУ в операторной форме дифференциальные уравнения становятся алгебраическими, то с ними можно оперировать совершенно так же, как с линейными уравнениями для установившегося режима.

Обозначим соответственно

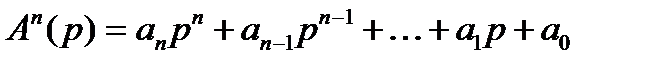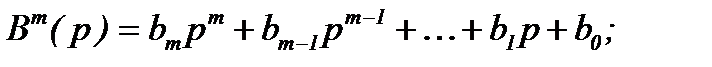; - полиномы n^-ой и m^-ой степени от р.

Тогда передаточная функция по задающему воздействию равна 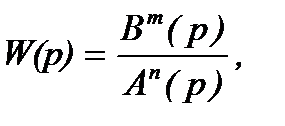(1.5)

где Аⁿ(р)=0 – характеристическое уравнение.

Если известны полюсы р_i и нули q_i функции W(p), соответствующие корням Aⁿ(p=0) и B^т(p)=0, то выражение (1.5) можно записать как

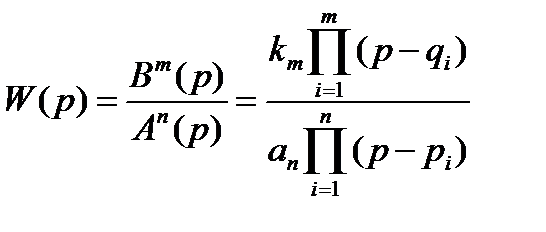. (1.6)

Предполагается, что полиномы Aⁿ(p) и B^m(p) не имеют общих корней и дробь (1.6) не может быть сокращена.

Найдём переходную функцию при входном единичном ступенчатом воздействии

х_ВХ(t)=1(t),тогда Х_ВХ(р)= 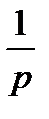. (1.7)

Вычислим 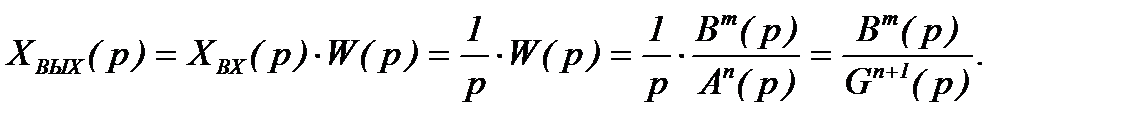(1.8)

Перейдём к оригиналу.

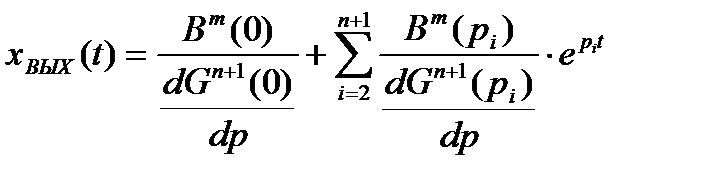, (1.9)

где р_i – корни уравнения Gⁿ⁺¹(p)=0.

Здесь предполагается, что функция W(p) не имеет кратных полюсов и что n>m.

Дата добавления: 2014-12-25