Понятие о частотных характеристиках

Как известно, полное решение общего дифференциального уравнения САУ складывается из двух составляющих:

1. Свободной составляющей, которая находится из решения однородного дифференциального уравнения (характеристического уравнения)

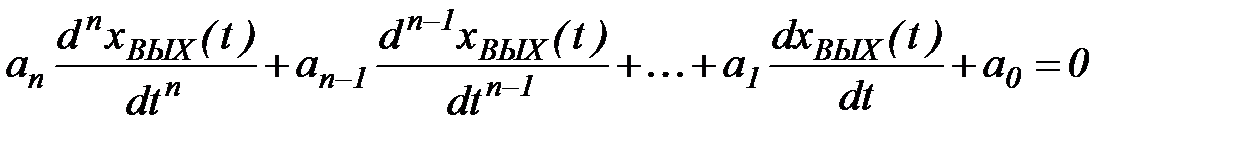. (1.10)

2. Вынужденной составляющей (частное решение), которая полностью определяется законом изменения во времени внешнего воздействия на САУ.

Удобно рассматривать динамику САУ (рисунок 1.1) или звена САУ при гармоническом изменении входной величины

.

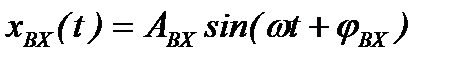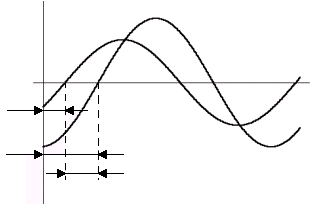
Тогда спустя некоторое время после начала действия X_ВХ на выходе системы установятся гармонические колебания той же частоты, что и частота входного воздействия, но имеющие другую амплитуду и фазу, т.е. вынужденную составляющую X_ВЫХ.

х_ВЫХ

х_ВХ

j_ВХ

j_ВЫХ

j

wt

Рисунок 1.3 – Входное и выходное значения

Очевидно, что при подаче на вход системы воздействия с той же амплитудой A_ВХ и начальной фазой j_ВХ, но другой частоты на выходе системы амплитуда A_ВЫХ и фаза j_ВЫХ будут иные.

Пример 1.1.

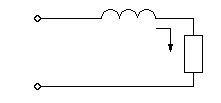
u = U_msinwt

L

i

R

Установившейся ток

в данном случае I_m и j являются функцией w.

Зависимость относительной амплитуды выходной величины от частоты называют амплитудно-частотной характеристикой (АЧХ) САУ

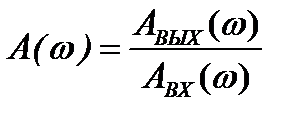- АЧХ. (1.11)

Зависимость сдвига фаз между гармоническими колебаниями выходной и входной величины от частоты называют фазо-частотной характеристикой (ФЧХ) САУ

А, j

А(w)

j(w)

w

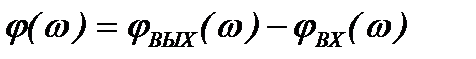- ФЧХ. (1.12)

Рисунок 1.4 – Зависимость АЧХ и ФЧХ от частоты

Совместное изменение амплитуды и фазы выходной величины от частоты можно получить, если представить синусоидальные функции в комплексной форме:

,

. (1.13)

АЧХ

ФЧХ

Если взять отношение выходной величины Х_ВЫХ(jw) к входной величине Х_ВХ(jw), то получим

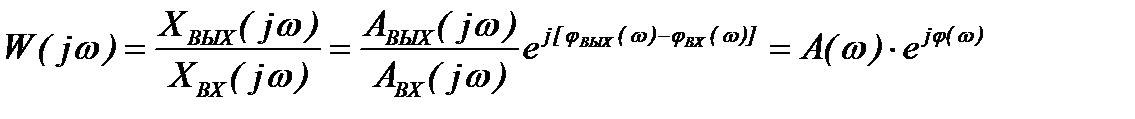. (1.14)

Комплексная функция W(jw) называется комплексным коэффициентом передачи САУ или амплитудно-фазовой частотной характеристикой (АФЧХ) САУ. Модуль этой функции представляет собой АЧХ, а аргумент – ФЧХ.

В общем случае W(jw) может быть представлен в виде числа

, (1.15)

где P(w) – называется вещественной частотной характеристикой САУ (ВЧХ);

Q(w) – называется мнимой частотной характеристикой САУ (МЧХ).

Между собой ВЧХ, МЧХ и АЧХ, ФЧХ связаны

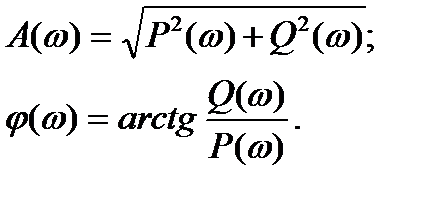
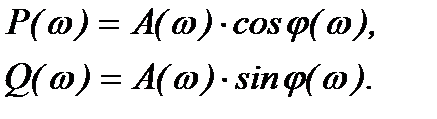(1.16)

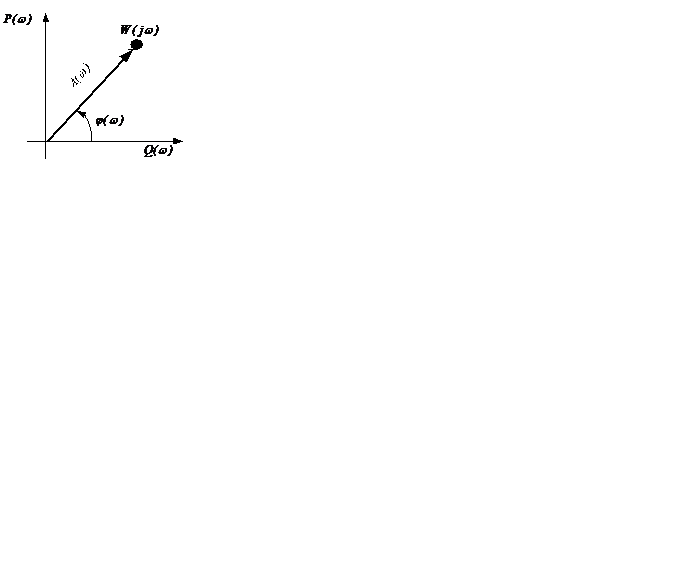График 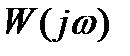называется годографом - год =

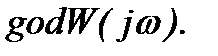
АФЧХ тесно связана с передаточной функцией САУ. При синтезе и анализе систем используются частотные методы, для этого к уравнению (1.1) следует применить преобразование Фурье. Для получения АФЧХ расчетным путем необходимо в передаточной функции звена или САУ положить Рисунок 1.5 – АЧХ, ФЧХ и p = jw.

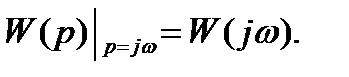ВЧХ,МЧХ

Пример 1.2.

Для функции , ,

должно быть .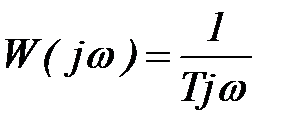

Пусть входная величина изменяется по синусоидальному закону, тогда:

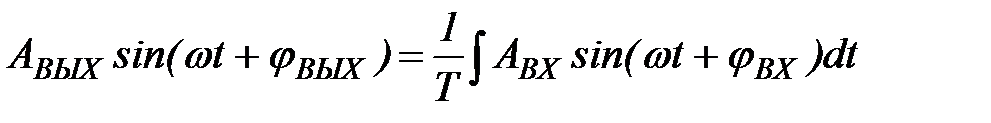, (1.17)

или в комплексной форме

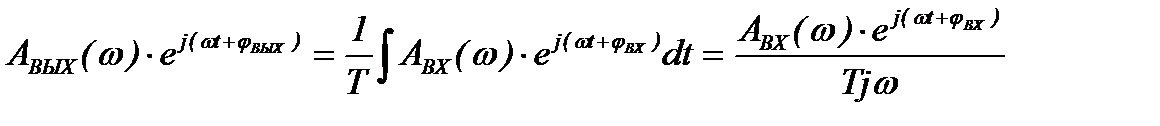, (1.18)

тогда

.

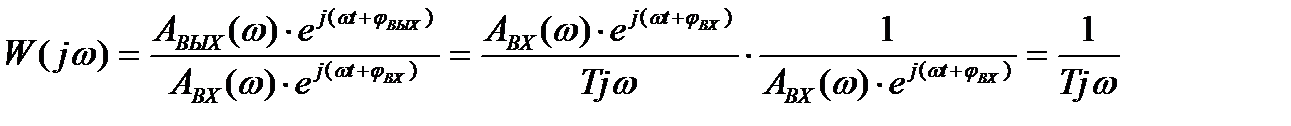(1.19)

Таким образом, действительно АФЧХ получилась из передаточной функции заменой p = jw, в общем случае можно записать:

W(jw) = [W(p)]_{р = jw}. (1.20)

Дата добавления: 2014-12-25