Алгебраїчні критерії стійкості САК

Обчислення коренів є простим для характеристичного рівняння першого та другого порядку. Для рівнянь третього та четвертого порядку загальні вирази для коренів громіздкі та незручні у використанні. Загальні вирази для коренів рівнянь вищих порядків не існують.

Тому важливе значення мають правила, які дозволяють визначати стійкість системи без обчислення коренів характеристичного рівняння. Ці правила називають критеріями стійкості.

За допомогою критеріїв стійкості можна встановити, стійка система чи ні, а також з’ясувати, як впливають на стійкість ті чи інші параметри та структурні зміни в системі.

Усі критерії можуть бути розподілені на алгебраїчні та частотні.

До алгебраїчних належать критерії Рауса, Гурвіца, Льєнара-Шипара. До частотних - критерії стійкості Михайлова, Найквіста.

Алгебраїчні критерії дозволяють судити про стійкість САК за коефіцієнтами характеристичного рівняння (6.6).

Зазначимо спочатку, що необхідною умовою стійкості системи будь-якого порядку є додатність усіх коефіцієнтів характеристичного рівняння, тобто

(6.7)

Для систем першого та другого порядків необхідна умова (6.7) є і достатньою умовою стійкості.

Для систем третього та вищих порядків додатність коефіцієнтів є необхідною умовою, але недостатньою.

Критерій стійкості Гурвіца. Цей критерій був запропонований 1895 року німецьким математиком О.Гурвіцем у вигляді визначників, що складаються за коефіцієнтами характеристичного рівняння замкнутої системи.

Спочатку будують головний визначник Гурвіца за таким правилом: по головній діагоналі визначника зліва направо виписують усі коефіцієнти характеристичного рівняння від a_n-1 до a₀ у напрямі зменшення індексів. Стовпці вгору від головної діагоналі доповнюють коефіцієнтами з індексами, що послідовно зменшуються, а стовпці вниз - коефіцієнтами з індексами, що послідовно збільшуються. Місця у визначнику, що залишилися, заповнюють нулями. Тобто визначник має вигляд:

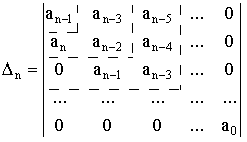(6.8)

Відкреслюючи у головному визначникові Гурвіца, як показано пунктиром, діагональні мінори, отримуємо визначники Гурвіца нижчого порядку:

(6.9)

Критерій стійкості Гурвіца формулюється таким чином: для того, щоб система автоматичного управління була стійкою, необхідно та достатньо, щоб усі визначники Гурвіца були додатними.

В останньому стовпці головного визначника Гурвіца (6.8) від нуля відрізняється лише один коефіцієнт a₀, тому

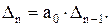(6.10)

Звідси видно, що при a₀ > 0 для перевірки стійкості системи достатньо знайти лише визначники Гурвіца від D₁ до D_n-1 (головний визначник D_n обчислювати непотрібно).

Якщо всі визначники нижчого порядку додатні, то система знаходиться на межі стійкості, коли головний визначник дорівнює нулю, тобто

(6.11)

Це можливо у двох випадках: a₀ = 0 чи D_n-1 = 0.

Використовуючи критерій Гурвіца, можна за заданими параметрами системи прийняти за невідомий будь-який один параметр (наприклад, коефіцієнт підсилення) та визначити його граничне (критичне) значення, при якому система буде знаходитися на межі стійкості.

Приклад. Характеристичне рівняння замкнутої системи має вигляд

де a₄=5; a₃=3; a₂=6; a₁=2; a₀=1.

Дослідити стійкість системи за критерієм Гурвіца і визначити критичний коефіцієнт підсилення системи.

Усі коефіцієнти рівняння додатні. Визначник Гурвіца матиме вигляд:

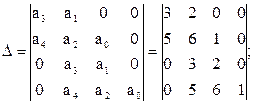
Значить, система стійка.

Визначимо критичне значення коефіцієнта a₀, прийнявши його за невідомий параметр:

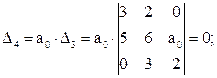a₀ ×(3×6×2 - 5×2×2 - 3×a₀×3) = 0; a₀ ×(16 - 9×a₀) = 0;

a₀^кр= 16/9, тобто при a₀> 16/9 система стає нестійкою.

Критерій стійкості Льєнара-Шипара.Критерій, запропонований 1914 року П. Льєнаром та Р. Шипаром, є однією з модифікацій критерію Гурвіца:

Якщо додатні всі коефіцієнти характеристичного рівняння замкнутої системи, то для її стійкості необхідно та достатньо, щоб були додатними всі визначники Гурвіца з парними або непарними індексами.

Тобто для стійкості САК необхідно та достатньо виконання таких нерівностей:

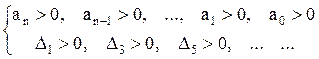(6.12)

або

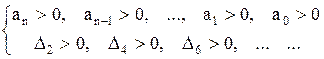(6.13)

Критерій Льєнара-Шипара потребує розкриття меншого числа визначників, ніж критерій Гурвіца, і тому зручніший для дослідження стійкості САК високого порядку.

Дата добавления: 2014-12-25