II. Вопросы для подготовки к коллоквиуму №1

I. Вопросы для подготовки к контрольной работе

Для развития и контроля владения компетенциями

Методические рекомендации

Вопросы, выносимые на обсуждение

1. Базис и ранг системы векторов.

2. Обратная матрица, методы ее нахождения.

3. Критерий совместности системы линейных уравнений.

4. Методы решения систем линейных уравнений.

5. Фундаментальная система решений системы линейных уравнений.

Для подготовки к занятию дома

1. Подготовьтесь к контрольной работе, используя теоретические задания для развития и контроля владения компетенциями.

2. Просмотрите решенные ранее задания по разделу «Основы линейной и векторной алгебры», обратите особое внимание на разобранные примеры решения типовых задач.

3. Изучите еще раз выполненные задания индивидуальных домашних заданий, обратите внимание на сделанные замечания преподавателя при их проверке и сделайте работу над ошибками.

4. Прорешайте примерный вариант контрольной работы, приведенный ниже.

На занятии по указанию преподавателя решите предложенный Вам вариант контрольной работы.

Дома

1. Подготовьтесь к коллоквиуму по вопросам приведенным ниже.

2. Пройдите предварительное компьютерное тестирование в указанное преподавателем время.

3. Сдайте коллоквиум по графику, предложенному преподавателем.

Рекомендуемая литература

[1] глава 2, глава 3.

[2] часть 1 глава I § 5, глава IV.

[3] часть I глава 2 §§ 8 – 9.

[4] часть I занятия 15 – 16.

Теоретические задания

1. Линейные операции над векторами.

2. Скалярное произведение векторов и его приложения.

3. Векторное произведение векторов и его приложение.

4. Смешанное произведение векторов и его приложения.

5. Определение линейной зависимости и линейной независимости системы векторов.

6. Базис и ранг системы векторов.

7. Координаты вектора в выбранном базисе.

8. Обратная матрица, условия ее существования.

9. Методы отыскания обратной матрицы.

10. Операции над матрицами.

11. Критерий совместности системы линейных уравнений.

12. Методы решения систем линейных уравнений.

13. Нахождение фундаментальной системы решений системы линейных уравнений.

Тема «Основы линейной и векторной алгебры»

1. Методы математики и ее значение для прикладных наук. Основные разделы современной математики.

2. Матрицы, основные определения.

3. Действия над матрицами: сумма, произведение матрицы на число, произведение матрицы на матрицу.

4. Определение определителя квадратной матрицы. Определители второго и третьего порядков.

5. Свойства определителей.

6. Миноры и алгебраические дополнения.

7. Вычисление определителя -го порядка.

8. Скаляры и векторы, основные определения. Линейные действия над векторами: сумма, разность, произведение вектора на число.

9. Линейная зависимость системы векторов, базис и ранг системы векторов, координаты вектора.

10. Скалярное произведение двух векторов, длина вектора, угол между векторами, условие ортогональности векторов.

11. Векторное произведение векторов: определение, свойства, вычисление, приложения.

12. Смешанное произведение векторов: определение, свойства, вычисление, приложения.

13. Ранг матрицы, его вычисление с помощью элементарных преобразований.

14. Вычисление ранга матрицы методом окаймления миноров.

15. Обратная матрица. Нахождение обратной матрицы с помощью алгебраических дополнений.

16. Вычисление обратной матрицы путем присоединения единичной.

17. Системы линейных уравнений. Основные определения.

18. Метод Гаусса решения систем линейных уравнений.

19. Критерий совместности систем линейных уравнений.

20. Матричный метод решения систем линейных уравнений.

21. Метод Крамера решения систем линейных уравнений.

22. Однородная система линейных уравнений, условие существования ненулевых решений.

23. Линейные пространства. Понятие n -мерного вектора. Примеры векторных пространств.

24. Определение линейного оператора, примеры.

25. Матрица линейного оператора, определение и нахождение.

26. Собственные векторы и собственные значения линейного оператора, их нахождение.

Практические задания

для развития и контроля владения компетенциями

Примерный вариант контрольной работы № 1

1. Найдите угол между векторами и , если , , .

2. Найдите какой-нибудь базис и ранг системы векторов , , , .

3. Решите матричное уравнение .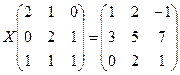

4. Исследуйте и решите систему уравнений .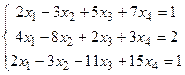

5. Решите систему линейных уравнений методом Крамера и матричным способом

.

6. Найдите фундаментальную систему решений системы линейных уравнений

.

Дата добавления: 2014-12-26