
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Для развития и контроля владения компетенциями
|
|
|
|
Коллоквиум №4
Для развития и контроля владения компетенциями
Темы «Функции нескольких переменных. Дифференциальные уравнения»
1. Функции нескольких переменных, основные определения (область определения, область значения, график функции двух переменных, линии и поверхности уровня).
2. Частные производные первого и более высоких порядков.
3. Экстремум функции двух переменных: определение, необходимое и достаточное условия экстремума.
4. Условный экстремум. Метод множителей Лагранжа.
5. Полный дифференциал и его приложение к приближенным вычислениям.
6. Задачи, приводящие к понятию кратных и криволинейных интегралов: определения, свойства, вычисление, приложения.
7. Задачи, приводящие к дифференциальным уравнениям.
8. Определение дифференциального уравнения, его порядка, общего и частного решений дифференциального уравнения.
9. Дифференциальные уравнения первого порядка с разделяющимися переменными.
10. Дифференциальные уравнения первого порядка: однородные, сводящиеся к однородным.
11. Дифференциальные уравнения первого порядка: линейные, уравнения Бернулли.
12. Дифференциальные уравнения первого порядка в полных дифференциалах. Уравнения сводящиеся к уравнениям в полных дифференциалах.
13. Решение дифференциальных уравнений с помощью рядов.
14. Дифференциальные уравнения второго и более высоких порядков, случаи понижения порядка.
15. Алгебраическая форма записи комплексного числа, действия над комплексными числами в алгебраической форме.
16. Тригонометрическая форма записи комплексного числа. Геометрическая интерпретация модуля и аргументы комплексного числа. Действия над комплексными числами в тригонометрической форме.
17. Перевод комплексных чисел из алгебраической формы записи в тригонометрическую и обратно.
18. Линейные дифференциальные уравнения второго порядка: однородные и неоднородные, структура их общих решений. Обобщение результатов для линейных дифференциальных уравнений n-го порядка.
19. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Характеристическое уравнение, построение общего решения.
20. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Отыскание их частного решения.
21. Понятие о системах дифференциальных уравнений.
22. Дифференциальные уравнения с частными производными: основные понятия.
Практические задания
Ответьте на приведенные ниже вопросы тестовых заданий:
1. Установите соответствие между дифференциальным уравнением и его общим интегралом.
1. 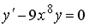 2.
2. 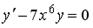 3.
3. 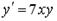
Варианты ответов: 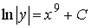
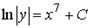

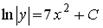
2. Общий интеграл дифференциального уравнения 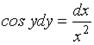 имеет вид…
имеет вид…
Варианты ответов: 1. 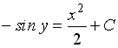 ; 2.
; 2. 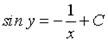 ; 3.
; 3.  ; 4.
; 4. 
3. Дано дифференциальное уравнение  при
при  . Тогда интегральная кривая, которая определяет решение этого уравнения, имеет вид…
. Тогда интегральная кривая, которая определяет решение этого уравнения, имеет вид… 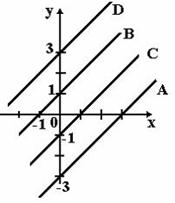
4. Решением уравнения 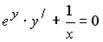 является функция …
является функция …
Варианты ответов: 1. 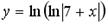 ; 2.
; 2. 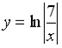 ; 3.
; 3. 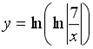 ; 4.
; 4. 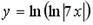
5. Дано дифференциальное уравнение 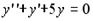 . Тогда соответствующее ему характеристическое уравнение имеет вид …
. Тогда соответствующее ему характеристическое уравнение имеет вид …
Варианты ответов: 1.  ; 2.
; 2.  ; 3.
; 3. 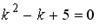 ;
;
4. 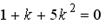
6. Общее решение линейного однородного дифференциального уравнения второго порядка с равными действительными корнями характеристического уравнения  имеет вид …
имеет вид …
Варианты ответов: 1. 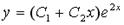 ; 2.
; 2.  ; 3.
; 3.  ;
;
4. 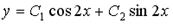
7. Общее решение линейного однородного дифференциального уравнения второго порядка с различными действительными корнями характеристического уравнения  и
и  имеет вид …
имеет вид …
Варианты ответов: 1. 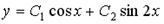 ; 2.
; 2. 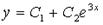 ; 3.
; 3. 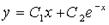 ;
;
4. 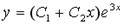
8. Решением уравнения первого порядка  является функция …
является функция …
Варианты ответов: 1. 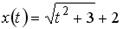 ; 2.
; 2.  ; 3.
; 3. 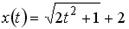 ;
;
4. 
9. Установите соответствие между дифференциальным уравнением и общим видом его частного решения
1. 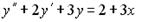
2. 
3. 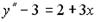
Варианты ответов: 1.  ; 2.
; 2.  ;
;
3. 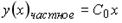 ; 4.
; 4.  ; 5.
; 5. 
10. Установите соответствие между дифференциальным уравнением и общим видом его частного решения …
1. 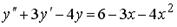 ; 2.
; 2.  ; 3.
; 3. 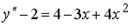
Варианты ответов: 1. 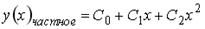 ; 2.
; 2. 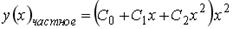
3.  ;4.
;4. 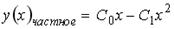 ;
;
5. 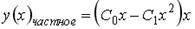
11. Установите соответствие между дифференциальным уравнением и его характеристическим уравнением …
1.  ; 2.
; 2. 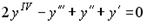 ; 3.
; 3. 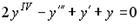
Варианты ответов: 1. 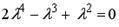 ; 2.
; 2.  ; 3.
; 3. 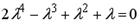 ;
;
4. 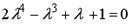 ; 5.
; 5. 
12. Общим решением линейного дифференциального уравнения с постоянными коэффициентами и характеристическими корнями 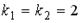 ,
,  является …
является …
Варианты ответов: 1. 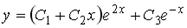 ; 2.
; 2.  ;
;
3. 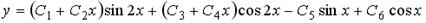 ;
;
4. 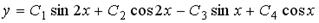
13. Общим решением линейного дифференциального уравнения с постоянными коэффициентами и характеристическими корнями 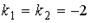 ,
,  является …
является …
Варианты ответов: 1. 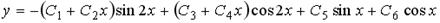 ;
;
2.  ; 3.
; 3. 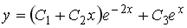 ;
;
4. 
14. Общим решением линейного дифференциального уравнения с постоянными коэффициентами и характеристическими корнями 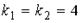 ,
, 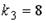 является …
является …
Варианты ответов: 1.  ;
;
2. 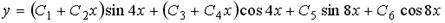 ;
;
3.  ; 4.
; 4. 
15. Укажите дифференциальное уравнение первого порядка.
Варианты ответов: 1. 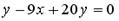 ; 2.
; 2.  ; 3.
; 3. 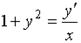 ; 4.
; 4. 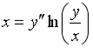
16. Укажите дифференциальное уравнение первого порядка.
Варианты ответов: 1. 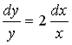 ; 2.
; 2.  ; 3.
; 3. 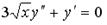 ;
;
4. 
17. Порядок дифференциального уравнения 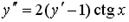 можно понизить заменой …
можно понизить заменой …
Варианты ответов: 1.  ; 2.
; 2.  ; 3.
; 3. 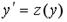 ; 4.
; 4. 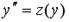
18. Уравнение 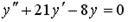 является …
является …
Варианты ответов: 1. линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами;
2. дифференциальным уравнением с разделяющимися переменными;
3. дифференциальным уравнением Бернулли;
4. линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами
19. Уравнение 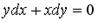 является …
является …
Варианты ответов: 1. линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами;
2. линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами;
3. дифференциальным уравнением первого порядка с разделяющимися переменными;
4. дифференциальным уравнением Бернулли
20. Уравнение  является …
является …
Варианты ответов: 1. линейным неоднородным дифференциальным уравнением 1 порядка;
2. уравнением Бернулли;
3. однородным дифференциальным уравнением;
4. уравнением с разделяющимися переменными.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 720; Нарушение авторских прав?; Мы поможем в написании вашей работы!