Формализм химической термодинамики

Продвинуться к поставленной цели поможет предположение о частичном равновесии. Пусть в системе реагентов установились все виды термодинамического равновесия (исчезли пространственные перепады давления, концентраций, температуры) и остались лишь неравновесные значения активностей реагентов. Пусть оставшиеся неуравновешенные химические компоненты претерпевают изменения в соответствии с реакциями:

ν₁R₁+ν₂R₂+…ν_iR_i → ν_i+1R_i+1 + … + ν_kR_k (2.36)

ν_i – стехиометрические коэффициенты. Если ν_i в левой части уравнения считать отрицательными, а в правой положительными, то из (2.36) получим:

K

Σ ν_iR_i = 0, это - стехиометрическое уравнение реакции (2.37).

i= 1

Пусть μ_i - молекулярная масса i-того – компонента.

Естественно считать, что для каждой конкретной реакции типа (2.37) должен существовать свой, характерный для данной реакции, параметр, ξ, определяющий её состояние на пути протекания реакции для массы реагентов:

m_i – m_io = ν_iμ_iξ

…………………

m_k – m_ko = ν_kμ_kξ (2.38)

или n_j – n_io = ν_iξ для числа молей

Здесь ξ ≡ координата реакции, степень её полноты 0 ≤ ξ ≤ 1

При ξ = 1 (один шаг реакции) прошел один эквивалент реакции. Складывая (2.38) и, помня о законе сохранения массы, получим для изолированной системы реагентов:

Это - стехиометрическое соотношение. ξ наряду с Р, Т при заданном m_io полностью характеризует состояние системы и, следовательно, является термодинамическим параметром.

Пример: H₂O = OH^-+ H⁺

n₁ = n₁₀ – ξ n₂ = n₃ = ξ,

т.е. ξ – это степень диссоциации в химическом смысле.

Дифференцирование (2.38) по времени дает:

или

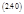
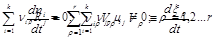Если в системе протекает r различных реакций типа (2.37), то появится дополнительный индекс ρ – номер реакции:

Здесь ξ_ρ – координата, V_ρ – скорость ρ -той реакции.

Сколько реакций линейно независимых, т.е. сколько степеней свободы ξ_ρ у системы? Ответ на это дает критерий Жуге: число независимых переменных равно рангу матрицы, составленной из стехиометрических коэффициентов ║ ν_iρ ║.

Вернемся к системе, в которой имеются и химические и термодинамические степени свободы: (Т, P, n_i) – могут изменяться, но одновременно по всей системе – так называемое частичноеравновесие. Рассмотрим сначала случай одной реакции. Пусть термодинамические потенциалы являются функцией, например T, V, n_i, или T, V, ξ при заданном n_io.

Объединим 1 и 2 начала термодинамики для закрытой системы.Из (2.22):

δQ^/ = TdS – δQ (2.44), а δQ выразим из (2.17): δQ=dU+pdV и подставим в (2.27):

Будем считать S=S (T, V, ξ), тогда:

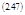аналогично, U=U(T, V, ξ):

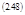Теперь из (2.45):

Независимые переменные dT и dV могут иметь любой знак, а ∂Q^/ всегда ≥ 0. Это значит, что выражения в скобках при dT и dV равны нулю.

Таким образом:

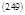Этот же результат можно получить короче, непосредственно используя уравнение Гиббса (если читатель его помнит):

где μ_i – химический потенциал i -того реагента (не путать с молекулярной массой в (2.38-2.42)!).

Сравнивая это выражение с выражением для dU из (2.45), получим формулу (2.45) в несколько более общем виде:

Производные от потенциалов по координате называются химическим сродством реакции. Обозначая его буквой А, получим из (2.49) или (2.51):

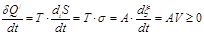где V – скорость реакции.

Это важное соотношение называется неравенство де-Донде (1937 г.).

В чем его интерес:

Если А >0, то V >0

Если А <0, то V <0

Если А =0, то AV =0, т.е. реакция обратима, а, значит, V =0. Итак, V имеет тот же знак, что и А и обращается в 0 тогда, когда А =0. Обратное же, вообще говоря, не верно: V =0 может означать истинное равновесие, когда А =0, но может и ложное, когда А ≠0, а реакция не идет из-за кинетических ограничений (без катализатора, фермента).

Итак, А =0 является необходимым и достаточным условием истинного равновесия. А (Т,V,ξ)=0 – уравнение, определяющее некую поверхность ξ=ξ(TV) на которой имеется равновесие, и которая отделяет область с А <0, от области А >0 (рис. 2.4).

Рис. 2.4

Но особую ценность неравенство де-Донде приобретает для случая нескольких одновременных в одном месте реакций:

При этом, используя (2.24) получим

А_ρ – сродство ρ -той реакции.

Здесь неравенство относится лишь к сумме! И отсюда возникает принципиально новый момент.

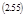Отдельные слагаемые суммы A_ρV_ρ могут теперь иметь отрицательный знак! Но A_ρV_ρ <0 означает, что ρ -тая реакция в данной системе идет в сторону, противоположную той, которую ей диктует её собственное (невозмущенное сопряжением) сродство, т.е. куда она шла бы, если бы была изолированной. Здесь нет противоречия со вторым началом термодинамики. Положительность полной функции диссипации обеспечивается при этом большой величиной σ_ρ «сопрягающих» реакций. Например для r =2: A₁V₁ + A₂V₂ ≥0. Пусть │ A₁V₁ │>│ A₂V₂ │, тогда A₂V₂ может быть <0, но при этом появляется ограничение на скорость сопряженной реакции:

Реакция 1 называется сопрягающей, 2 – сопряженной.

Таким образом А_ρ приобретает важное значение для анализа V_ρ.

Физический смысл химического средства ρ – той реакции достаточно прост: это мера скорости падения свободной энергии системы реагентов в процессе протекания ρ -той реакции. Численно его значение совпадает с изменением свободной энергии реакции, когда она продвигается на один шаг (ξ = 1), т.е. когда прореагируют стехиометрические количества реагентов. Но знак его по определению противоположен: чем сильнее убывает свободная энергия системы, тем более положительна сила, движущая процесс, т.е. А_ρ.

В общем случае, для любого числа независимых реакций

(2.56)

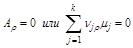Условия истинного равновесия:

Это соотношение не следует путать с формулой (2.39), они имеют совершенно разный смысл.

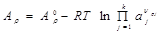Значение А_ρ, как и ∆G_ρ, выражается через стандартную часть, соответствующую превращению реагентов при стандартных условиях (нормальном давлении, комнатной температуре и активности реагентов, равных 1 м/л) и добавку, учитывающую отличие активностей от стандартных значений:

Эта формула наглядно отражает очевидный факт: чем больше активность субстратов реакции, входящих в левую часть уравнения (2.30) (т.е. имеющих отрицательные ν_ρi), тем больше сродство.

Первый член в (2.58), энтальпийный по своей природе, отражает собственную энергетику акта взаимодействия реагентов, а второй, энтропийный, отвечает за вероятность встречи реагентов.

Подставляя (2.58) в условия равновесия реакций (2.57), получим:

Т.к. константа равновесия по определению

то

где μ_oj – стандартная часть химического потенциала j - того реагента:

Эти формулы пригодятся нам в дальнейшем.

Итак, соотношение де-Донде (2.55) указывает на принципиальную возможность термодинамического сопряжения двух реакций, т.е. на обращение скорости сопряженной реакции за счет большого сродства сопрягающей реакции. Действительно, в живых системах протекание процессов против их естественного сродства это типичное явление, делающее возможным возникновение и поддержание устойчивого неравновесия в целом ряде важных клеточных систем за счет сопряжения их со спонтанно протекающими процессами. Множество примеров мы рассмотрим в дальнейшем. Соотношение де-Донде показывает, что в этом нет противоречия со вторым началом термодинамики. Посмотрим, однако, что говорит о такой возможности формальная химическая кинетика, основанная на законе действующих масс.

Рассмотрим пример простейшей химической реакции превращения веществ R₁ и R₂ в R₃.

Её скорость V=dn₃/dt (n – число молей) это разность скоростей прямой и обратной реакции:

где К _1,2 и К ₂ контрасты скоростей прямой и обратной реакции, [ R_i ] – активности реагентов а ν₁, ν₂, ν₃, положительные числа. Преобразуем (2.64)

Здесь К – константа равновесия, равная К _1,2/ К ₃.

С другой стороны K можно связать с А по (2.61) и (2.58):

и получить из (2.66):

V=V₀(1-e^-A/RT) (2.67)

Это общее выражение можно получить для любого другого вида реакций. О чем оно говорит? О том, что знак V всегда совпадает со знаком А! Иначе говоря, термодинамика разрешает сопряженной реакции идти против её сродства, а кинетика не позволяет этого. Парадокс?! Нет. Просто условие возможности сопряжения (2.55) являются необходимым, но не достаточным для реального сопряжения. Чтобы сопряжение в смысле изменения направления сопрягаемой реакции действительно произошло необходим специальный физический механизм изменения знака сродства А ₂ за счет части сродства А ₁, передаваемой из первой реакции во вторую.

Возможны 2 типа механизмов обеспечивающих такое взаимодействие.

1. Энергетический механизм. Это передача части уменьшения свободной энергии системы при протекании первой реакции реагентам второй в виде какого-то вида работы над ними, увеличивающей их внутреннюю энергию или энтальпию, т.е. стандартную часть средства, А ₂₀. Это может быть деформация реакционного комплекса реагентов второй реакции, создание электрического поля, облегчающего взаимодействие реагентов и т.п. Макромолекулы ферментов, осуществляющих сопряжение, могут реализовать такие процессы.

2. Вероятностный (энтропийный) механизм. Это затрата части реализуемой свободной энергии первой реакции на изменение активности реагентов второй реакции, т.е. увеличение второго, этропийного члена в сродстве А ₂. Тривиальным примером является увеличение концентрации реагентов второй реакции, если обе реакции имеют общий продукт. Менее тривиальным, но более интересным примером является изменение при протекании первой реакции коэффициентов активности второй. Так, первая реакция может так изменить конфигурацию или свойства среды (поверхности), где протекает вторая реакция, что при той же концентрации её реагентов они станут более подвижными (например, десорбируются с поверхности) и увеличат вероятность своего участия в реакционном акте.

2.3 Элементы линейной неравновесной термодинамики.

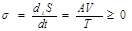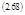Прежде, чем продвигаться дальше, сделаем естественные обобщения. А, введенное нами как химическое средство реакции в соотношение де-Донде:

равное по определению – (∂F/∂ξ)_{T, V} =…, может иметь более общее значение, т.к. (2.68) и ∂F/∂ξ характеризует не только химическое превращение. Вытекающая из (2.68) связь знаков А и V характерна для большого круга процессов, когда скорость процесса соразмерна его движущей силе. Так бывает при диффузии, электро- и теплопроводимости, когда соответствуют не только знаки А и ν, но существует и пропорциональность между потоком некой величины и причиной («силой») его возвышающей: закон Ома j~grad φ; закон Фурье j=grad T; закон Фика j = grad c; закон Ньютона j=∆C р.

Поэтому целесообразно ввести понятие «обобщенной силы» или сродства Х и обобщенной скорости процесса («потока») J. Опыт учит, что

J ~ X (2.69)

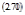Если в системе одновременно протекает r процессов, то естественно (2.63) и (2.70) обобщить до линейной комбинации:

Соотношение (2.71) – обобщение опыта. Оно не может быть доказано в рамках термодинамики и является феноменологическим линейным соотношением. Но если уж оно справедливо, то термодинамика позволяет сделать дополнительные утверждения. Для небольших отклонений от равновесия Онзагер (1931 г.) установил соотношение взаимности:

т.е. матрица L_in – диагонально симметрична.

В общем случае

L_jj >0, L_ik²<L_iiL_kk (2.74)

Если, например: r =2,

то σ = L₁₁X₁²+(L₁₂+L₂₁)X₁X₂+L₂₂X₂² >0

Отсюда:

знак L₁₂ – любой.

Если после этого обобщения вернуться к химическим реакциям, то, положив Х=А/Т, J=V, получим

J_хим=L·X=LּА/Т· (2.76)

Теперь утверждение о том, что скорость химической реакции пропорциональна химическому сродству, получило феноменологически обобщенное подкрепление.

Возникает законный вопрос – при каких условиях линейные соотношения, справедливы?

Определим эти условия, сравнив два выражения для скорости – (2.76) из линейной термодинамики и точное (2.67) из химической кинетики.

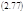Сопоставляя скорости реакций из этих выражений, видим, что они равны лишь при условии A/RT <<1, когда (2.67) можно разложить в ряд:

К сожалению условие (2.77) выполняется реже, чем хотелось бы: при комнатной температуре RT ≈ 0,6 кк/м = 3,5 кДж/м = 25 мЭв, а для многих биохимических реакций А ≈ 1-2 кк/м и выше, т.е. А ≥ RT!

Однако, когда это неравенство не выполняется и, притом, сильно, то процесс можно представить себе как идущий через ряд последовательных стадий, каждую из которых можно охарактеризовать своим сродством А_ρ и своей координатой ξ_ρ:

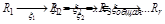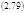Если промежуточные вещества нестойки (а только в этом случае реакция идет насквозь!), то должно быстро устанавливаться состояние, при котором:

т.е. сохраняется линейность V и A_ρ (если A_ρ<<RT).

Т.е. мы остаемся в рамках применимости линейных соотношений для этого (особого!) стационарного состояния (V₁=…V _общ.) хотя общее A ≥ RT.

2.3 Стационарное состояние

Дата добавления: 2014-12-26