Теорема Пригожина

Неравновесной системы

Только что мы рассмотрели стационарное состояние промежуточных продуктов химических реакций. Познакомимся подробнее с общими свойствами стационарного состояния, которое имеет такое же фундаментального значение для открытых систем, как состояние равновесия для изолированных систем.

Сформулируем некоторые важные положения. Для наглядности проведем рассуждение на конкретном примере, а затем обобщим результаты. Рассмотрим хорошо известную неравновесную систему «газ Кнудсена» (рис.2.5)

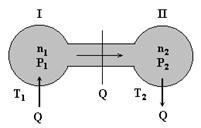
Рис. 2.5

В двух баллонах, связанных тонкой трубкой, находится газ. Концентрация газа, его давление и температура в баллонах n₁, P₁, T₁, и n₂, P₂, T₂, соответственно, газ может перетекать из одного баллона в другой через тонкую трубку. В условиях молекулярного течения плотность потока частиц, пропорциональна n·V, где V – средняя скорость частиц. В условиях динамического равновесия, когда потоки слева направо уравнялись с потоком справа налево:

n₁V₁=n₂V₂ (2.81)

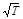Если при этом Т₁ и Т₂ различаются и фиксированы, то V_i; будучи ~ _i, будут различны, а значит из (2.81) и n_i будут различны. Будут отличаться и P(P=nkT).

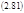Таким образом, стационарность, т.е. неизменность во времени всех параметров системы, в то же время не будет равновесием, т.к. n₁ ≠ n₂, P₁ ≠ P₂ (если T₁ ≠ T₂). Примем, что Т₁ > Т₂. Тогда через соединительную трубку будет перетекать поток тепла, т.к. при равном потоке частиц, частицы летящие слева более «горячие». Действительно, для поддержания Т₁ > Т₂ необходимо непрерывно подводить к левому баллону от внешнего нагревателя тепловой поток, мощностью δQ/dt, а от правого непрерывно отбирать в холодильник такой же поток тепла. Но δQ, подводимое к левому баллону при температуре Т₁, означает введение в систему потока энтропии d₁S / dt = δQ / dt∙T₁^-1, а отвод δQ, от правого баллона при температуре T₂ означает извлечение из системы потока энтропии d₂S / dt = δQ, / dt∙T₂^-1. Легко видеть, что

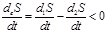Но энтропия системы, как и все остальные термодинамические параметры, в стационарном состоянии, должна быть неизменной. А это означает, что в стационарном состоянии скорость производства энтропии внутри системы σ = d_iS/dt из-за протекания в ней необратимого диссипативного процесса (в данном случае - переноса тепла от нагревателя к холодильнику) в точности компенсируется дефицитом поступления энтропии d_еS/dt из окружающей среды.

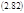Следует заметить, что любое текущее состояние газа Кнудсена описывается двумя независимыми параметрами: отношением температур Т₁/Т₂ и Р₁/Р₂ (или, что эквивалентно n₁/n₂). Первый параметр зафиксирован внешними условиями, а второй предоставлен сам себе, но в стационарном состоянии достигает вполне определенного значения, легко получаемого из (2.80):

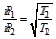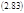или

Докажем теперь, что σ в стационарном состоянии достигает экстремального значения.

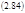По определению:

где Х_T – обобщенная сила, связанная с перепадом температур баллонов (например Т₁ – Т₂), Х_М – обобщенная сила, связанная с перепадом давления (например Р₁ – Р₂), J_T – поток тепла через систему, J_m – разностный поток частиц между баллонами. Из линейных соотношений (2.71):

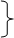J_T = L₁₁X_Т + L₁₂X_M

J_M = L₂₁X_T + L₂₂X_M

Здесь L_iK – онзагеровские коэффициенты.

Подставим (2.85) в (2.84) и учтем, что L₁₂ = L₂₁

σ = L₁₁X_T² + 2L₂₁X_TX_M + L₂₂X_M² (2.86)

Пусть, как и в нашем случае X_T=const. Тогда

Но в стационарном состоянии J_M =0. Следовательно

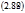Возьмем вторую производную от (2.83):

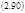Таким образом, диссипативная функция как функция от свободной переменной Х_М в стационарном состоянии достигает экстремума, а именно минимума. Мы доказали теорему И. Пригожина. Сформулируем её словесно: «Диссипативная функция открытой (неравновесной) системы, т.е. скорость диссипации свободной энергии, в стационарном состоянии достигает минимума совместимого с фиксированным значением обобщенной силы.» Этот минимум достигается за счет изменения свободной обобщенной силы, которой система «распоряжается» сама. Математическое выражение этой важной теоремы сводится к формулировке условия минимума σ как функции двух переменных;

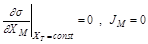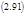и легко обобщается на случай большего числа переменных:

где j =1,2… k - индексы фиксированных обобщенных сил, i = k +1… r – индексы остальных, свободных сил и потоков. Стационарность заключается в исчезновении i – тых потоков.

Дата добавления: 2014-12-26