Поведение в окрестности стационарного состояния.

Если система в результате кратковременного воздействия (флуктуации некоторых обобщенных сил) выведена из стационарного состояния, т.е. σ получила положительное приращение ∆σ, то какова дальнейшая эволюция σ после флуктуации в виде двух компонент,

dσ =d_Xσ + d_Jσ, (2.92)

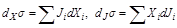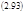где

Поведение d σ определяется двумя теоремами.

Теорема 1. Если справедливы линейные феноменологические уравнения, соотношения взаимности Онзагера и L_ij=const, (т.е. стационарное состояние и его окрестность недалеки от равновесия), то

d_Xσ = d_Jσ (2.94)

Доказательство:

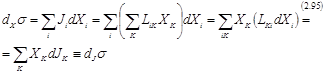Теорема 2: Если фиксирование обобщенных сил неизменно во времени, то во всей области справедливости термодинамики необратимых процессов

d_xσ ≤ 0 (2.96)

Доказательство этой теоремы в общем виде довольно громоздкое, и мы не будем его приводить; желающие могут ознакомиться с ним в книге [Пригожин].

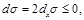Объединяя обе теоремы, получим в итоге:

т.е. σ самопроизвольно возвращается к исходному минимальному значению.

Значит, если стационарное состояние недалеко от равновесия, то оно устойчиво по отношению к малым флуктуациям. Если стационарное состояние сильно не равновесно или флуктуации велики в этом же смысле, то вывод системы из первоначального состояния может оказаться необратимым. Доказанные теоремы, таким образом не закрывают путь самопроизвольному развитию неравновесной системы как переходу из одного состояния в другое. Рис. 2.6 иллюстрирует это.

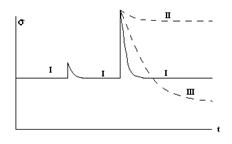
Рис. 2.6. Устойчивость состояния I к малым флуктуациям и возможные варианты «развития» системы (II, III) при больших возмущениях.

Теорема Пригожина и условия устойчивости стационарного состояния могут быть наглядно проиллюстрированы (рис. 2.7) для двух степеней свободы, при фиксированном значении Х₁.

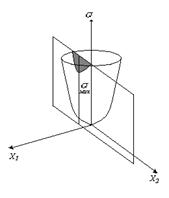
Рис. 2.7

Сечение параболоида плоскостью Х₁=Х₁₀ вырезает из него кривую σ(Х₂), имеющую минимум в точке Х₂=Х₂⁰. Это условный минимум, не равный нулю и соразмерный фиксированному значению Х₁₀.

Если же Х₁₀ «отпустить», то поиск минимума σ закончится опусканием в точку σ =0, при котором Х₁ =0, Х₂ =0 и стационарное состояние вырождается в состояние равновесия. В окрестности равновесия σ(Х₁,Х₂) представляет собой гладкий параболоид, однако при больших Х₁ или Х₂ на кривой могут появиться складки и карманы, создающие области со своими минимума σ, куда состояние системы может попасть при больших флуктуациях, как это показано на рис. 2.6.

Указанные теоремы можно рассматривать как обобщение принципа Ле-Шателье – Брауна. Этот принцип констатирует устойчивость равновесного состояния изолированной системы, утверждая, что процессы, вызываемые в системе внешними воздействиями, всегда направлены на уменьшение первоначального отклонения от состояния равновесия. Приведенные теоремы позволяют говорить о подобных свойствах неравновесной, но стационарной открытой системы. Многочисленные примеры такой устойчивости («гомеостаза») мы увидим при знакомстве с конкретными живыми системами и подсистемами. Однако многие из этих механизмов имеют общую термодинамическую природу, отражающую универсальные свойства открытой системы вблизи стационарного состояния. Эту мысль можно проиллюстрировать простыми примерами.

Рассмотрим простейшую открытую систему: плоскую полость с толщиной h с безграничной шириной. Пусть она помещена в безграничный раствор некоторого вещества, которое может проникать в полость через её боковые грани (рис.2.8.). Пусть проницаемость граней р₁ и р₂, а концентрация вещества слева и справа от полости низменны и равны а₁ и а₂, соответственно.

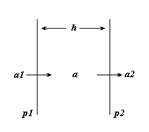
Рис. 2.8

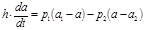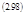Тогда для концентрации вещества, а, внутри полости можно записать балансовое уравнение:

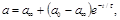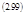Считаем, что внутри полости вещество быстро перемешивается, так что его концентрация по толщине полости одинакова. Решение уравнения (2.98) имеет вид:

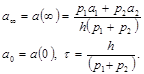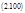где

Это решение имеет характерные особенности:

1. Через t >> τ a(t) выходит на асимптотический (стационарный) уровень, который не зависит от начального значения а.

2. Попытки изменить стационарное значение, а_∞, изменением а₁ и а₂ или р₁ и р₂ приведет лишь к ограниченному успеху. da_∞/da₁ и da_∞/da₂ меньше 1, а изменению а_∞ при вариации р₁ и р₂ также невелики, т.к. р₁ и р₂ входят и в числитель, и в знаменатель а_∞. Кинетика перехода от а₀ к а_∞ носит экспоненциальный характер.

Все эти три качества напоминают «гомеостаз» живой системы, хотя в конструкцию нашей простейшей модели не закладывались никакие специальные устройства, искусственно поддерживающие неизменность а_∞. Это свойство автостабилизации стационарного состояния возникает автоматически в любой открытой системе, в которой обобщенные потоки линейно связаны с обобщенными силами. Любое изменение а тут же вызывает соответствующее изменение притока и вывода вещества через границы системы, стабилизируя значение а.

Второй пример позволяет учесть возможные химические превращения в объеме полости, моделируя «желудок и переваривание» (рис 2.9.)

Рис. 2.9

Пусть слева от полости находится вещество А, с неизменной концентрацией а₁, а справа только В с неизменной концентрацией b₁, а в полости они превращаются друг в друга по законам реакции первого порядка с константами скоростей К ^/ и К ^//.

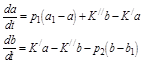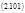Проницаемость левой грани к веществу А равна р₁, а правой грани к В равна р₂. Тогда кинетическое уравнение можно записать так:

Их решения имеют вид:

_,

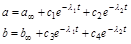
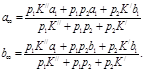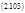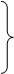где

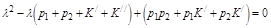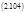λ₁, λ₂ – корни характеристического уравнения:

Как легко видеть, λ₁ и λ₂ положительны. Здесь также, как и в предыдущем случае, через время t> λ₁^-1, λ₂^-1 система «забывает» о начальном положении и выходит на стационарное значение а_∞ и b_∞, обладающие устойчивостью по отношению к изменению всех своих параметров. Однако, помимо этого свойства, напоминающего гомеостаз в живом объекте, данная система демонстрирует нетривиальную кинетику переходного процесса. При изменении параметров стационарные значения переходят к новым значениям тремя способами: монотонным и двумя немонотонными (рис. 2.10.) в зависимости от начальных условий и значений λ₁ и λ₂. Переходы такого типа характерны для многих биологических систем. Например, сложный переход с «овершутом» (тип 2) напоминает изменение уровня сахара в крови млекопитающих, а нетривиальный «ложный старт» (тип 3) – вариацию напряжения кислорода в корешках лука при изменении парциального давления О₂.

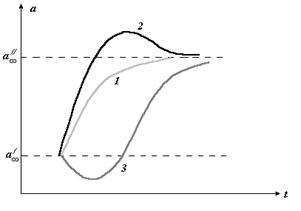
Рис. 2.10

Обычно предполагается, что такие сложные переходные процессы отражают работу специальных устройств контроля и регулирования. Но, как видим, это может быть простым свойством открытых неравновесных систем, в которых автостабилизация стационарного состояния происходит сама собой.

Вообще, следует сказать, что представление о необходимости существования сложных специальных устройств, регулирующих контроль и управление в живых клетках и тканях, вероятно, сильно преувеличено. Сложное «целесообразное» поведение живых объектов может быть обеспечено простыми механизмами, основанными на свойствах открытых систем и кинетики реакции, подчиняющихся закону действующих масс. А если скорости реакций определяются катализаторами (ферментами), то уже простейшие предположения о свойствах ферментов позволяют понять и описать всю сложность поведения биохимической системы.

Так, например, если вещество А способно участвовать в двух альтернативных превращениях по типу реакций первого порядка, давая два разных продукта В и С, то для их концентрации а, b, c, соответственно, можно записать:

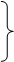
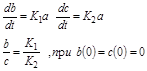Наблюдая за ростом концентрации веществ В и С, мы будем фиксировать b >> с, если К₁>>К₂. При большой концентрации вещества В можно даже не заметить в этих условиях присутствие вещества С. Однако, если реакции ферментативны, и неравенство К₁>>К₂ обусловлено высокой активностью фермента Е₁ при его концентрации значительно более низкой, чем концентрация фермента Е₂, то с ростом концентрации исходного вещества, может произойти насыщение скорости первой реакции. Если при этом константа К₂ остается неизменной, то нарастающая концентрация вещества С может значительно превысить концентрацию вещества В (рис 2.10). Создается ошибочное впечатление о наличии специального переключателя скоростей процессов при а=а*, которого на самом деле нет.

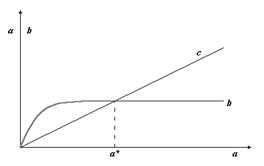Рис. 2.10

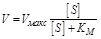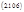При этом мы не делали никаких дополнительных предположений о свойствах ферментов, кроме тривиальной зависимости скорости ферментативной реакции от концентрации субстрата (уравнение Михаэлиса-Ментен):

где [ S ] – концентрация субстрата, К_М – константа Михаэлиса, зависящая лишь от молекулярных параметров фермента и субстрата.

В более общем случае, когда К_М может зависеть от концентрации субстрата и (или) других веществ, поведение системы может стать неизмеримо сложнее и способно описать большой класс реально наблюдаемых свойств биохимических процессов. При этом в основе кинетики процессов попрежнему лежит закон действующих масс, но константы скоростей перестают оставаться постоянными. Факторами, влияющими на активность ферментов, иногда выступают молекулы АТФ, но чаще циклические АМФ, концентрация которых в свою очередь контролируется гормонами.

В совокупности эти проявления обратных связей и элементов регулирования констант скоростей создают сложную и динамичную структуру системы взаимопревращений веществ в биохимических системах. Её анализ представляет собой сложную задачу. Однако есть несколько подходов, позволяющих значительно упростить её. Прежде все6го это два известных принципа упрощения вида сложной сети. Первый – принцип Либиха (принцип «узкого места»): в последовательной цепи превращений наибольшее влияние на скорость образования конечного продукта оказывает реакция с наименьшей скоростью. Второй – принцип Хиншельвуда: в системе альтернативных процессов важнейшими являются те, которые идут с наибольшими скоростями и остаются реакциями первого порядка (т.е. не насыщаются) в наибольшем диапазоне концентраций субстратов. Использование этих простых принципов позволяет исключить из сети превращений менее существенные.

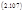Важным для дальнейшего упрощения является редукция системы, основанная на анализе временной иерархии процессов. Часто систему кинетических уравнений для концентрации реагентов Х системы можно разбить на три группы:

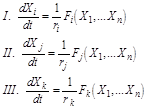где характерные времена τ_i, τ_j, τ_k для концентрации Х в группах реагентов I, II, III, соответственно, удовлетворяют условию

τ_i<<τ_j<<τ_k (2.108)

На интервале времен t>>τ_I концентрации реагентов группы I успевают достигнуть своих стационарных концентраций и их динамику можно описать алгебраическим уравнением:

F_i (X_i,…X_n)= 0 (2.109)

вместо дифференциального:

На интервале t>>τ_III концентрации реагентов группы III не успевают измениться и их можно считать постоянными, заданными в начальный момент:

X_k=X_k0=const (2.110)

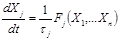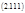В итоге исходная система редуцируется и на интервале t≈τ_i приобретает существенно меньший порядок:

Управление такой редуцированной системой значительно упрощается: за переменными группы I не нужно следить, а переменные группы III приобретают смысл управляющих препаратов. Живая природа в процессе эволюции не могла пройти мимо этой возможности, ибо подобное упрощение системы увеличивает её надежность. Этот принцип простоты остроумно сформулировал философ екатерининских времен Г.С. Сковорода, сказавший примерно следующее: «Слава тебе, боже, за то, что ты сделал все нужное простым, а все сложное – ненужным!»

Этот принцип должен давать организмам большие преимущества в борьбе за существование. Те же, кто его не успел использовать в ходе эволюции, должны были вымереть. Если это так, то должна сложиться парадоксальная ситуация: математическое моделирование живой биохимической системы должно быть проще, чем искусственного биохимического реактора с тем же количеством степеней свободы, т.к. последний ещё не прошёл естественного отбора.

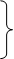Наглядным примером продуктивности использования вышеуказанного принципа простоты (точнее, принципа стационарных состояний, основанного на известной теореме А.Н. Тихонова) является история исследования системы гликолиза в живой клетке. Моделируя сложный метаболизм глюкозы, Чанс и Гарфинкель в середине прошлого века написали 22 дифференциальных уравнения и провели анализ их численных решений, использовав имеющуюся в их распоряжении вычислительную машину. Этот анализ не выявил ничего интересного. В то же время Молчанов и Сельков, не имея такой технической возможности, провели более интеллектуальную атаку на эту систему и смогли редуцировать её к двум уравнениям:

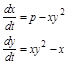где х и у концентрации Фруктозы-6-фосфата и АДФ, соответственно. Исследование системы (2.112) позволило предсказать возможность автоколебаний в системе гликолиза, которые в последствии и были обнаружены экспериментально.

Дата добавления: 2014-12-26