
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закон сохранения полной механической энергии
|
|
|
|
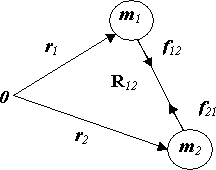 Пусть замкнутая система состоит из двух взаимодействующих друг с другом частиц. В соответствии с третьим законом Ньютона:
Пусть замкнутая система состоит из двух взаимодействующих друг с другом частиц. В соответствии с третьим законом Ньютона:
 ,
,
 где
где  – внутренние силы, действующие на частицу со стороны другой частицы.
– внутренние силы, действующие на частицу со стороны другой частицы.
Введем вектор  , где
, где 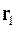 и
и  - радиус-векторы частиц (рис. 3.5).
- радиус-векторы частиц (рис. 3.5).
Запишем уравнения движения частиц:
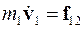 ,
,
 . (3.32)
. (3.32)
Умножим первое из этих уравнений на  , а второе на
, а второе на 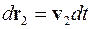 и сложим уравнения
и сложим уравнения
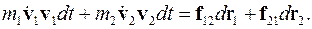 (3.33)
(3.33)
Левая часть этого соотношения - приращение кинетической энергии, а правая - приращение работы:
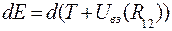

отсюда находим
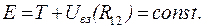 (3.34)
(3.34)
Здесь 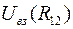 называется потенциальной энергией взаимодействия и зависит от расстояния между частицами. Для двух частиц, движущихся со скоростями
называется потенциальной энергией взаимодействия и зависит от расстояния между частицами. Для двух частиц, движущихся со скоростями 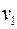 и
и  :
:
 (3.35)
(3.35)
Потенциальную энергию взаимодействия  в этом случае можно рассматривать как потенциальную энергию U одной частицы, находящейся в поле сил другой частицы.
в этом случае можно рассматривать как потенциальную энергию U одной частицы, находящейся в поле сил другой частицы.
Рассмотрим теперь систему, состоящую из n частиц, взаимодействующих с силами 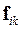 .
.
Уравнение движения i-той частицы
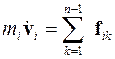 . (3.36)
. (3.36)
Если на частицу действует внешняя консервативная сила 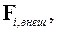 тогда уравнение движения примет вид
тогда уравнение движения примет вид
 (3.37)
(3.37)
Умножим (3.37) на  и сложим все уравнения, находим
и сложим все уравнения, находим
 .
.
отсюда следует, что полная механическая энергия сохраняется
 (3.38)
(3.38)
Закон сохранения полной механической энергии системы можно сформулировать следующим образом: Полная механическая энергия системы тел, на которые действуют только консервативные силы, остается постоянной.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 423; Нарушение авторских прав?; Мы поможем в написании вашей работы!