Главные моменты инерции

Момент инерции материальной точки относительно оси, совпадающей с осью X можно записать в виде

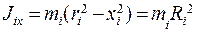(5.19)

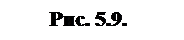
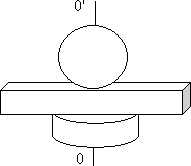Момент инерции твердого тела относительно этой оси равен сумме произведений масс материальных точек на квадраты расстояний от них до оси. Момент инерции тела сложной формы относительно оси OO’ равен сумме моментов инерции тел простой формы относительно данной оси (рис. 5.9).

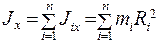(5.20)

Если ось X проходит через центр инерции (центр масс) твердого тела простой формы (стержень, диск, шар), то главные моменты инерции этого тела можно найти по формуле:

(5.21)

где r - плотность тела;

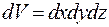- элемент объема, в котором заключена масса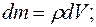

R – расстояние от элемента объема до оси.

Найдем момент инерции стержня относительно оси y. Длину стержня обозначим 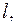его поперечный размер b (рис. 5.10).

Рис. 5.10.

Элемент объема стержня Интегрирование по х будем проводить в пределах от –l/2 до l/2:

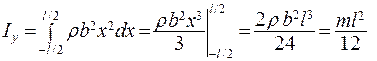(5.22)

где 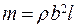- масса стержня.

Главные моменты инерции стержня: 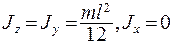. Толщина стержня предполагается малой по сравнению с его длиной.

Главные моменты инерции диска (рис. 5.11):

.

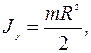
Главные моменты инерции шара: .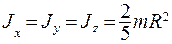

Теорема Гюйгенса – Штейнера

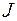Момент инерции тела относительно произвольной оси равен сумме момента инерции 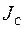относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела m на квадрат расстояния a между осями.

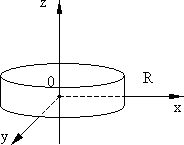
Рис. 5.11.

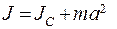(5.23)

Гюйгенс Христиан (1629 – 1695), голландский физик, механик, математик и астроном, родился в Гааге, учился в университетах Лейдена. Физические исследования в области механики, оптики, молекулярной физики. Решил задачу об определении центра колебаний физического маятника и его периода колебаний, установил законы, определяющие центростремительную силу. Исследовал столкновение упругих тел и вывел его законы.

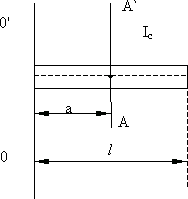
Пример: Найти момент инерции стержня относительно оси OO’, проходящей через край стержня перпендикулярно его оси (рис. 5.12):

.

.

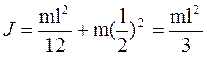Рис. 5.12.

Дата добавления: 2014-12-26