Потоком конус-цилиндрических тел

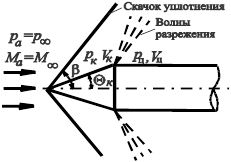Рис. 24. К методу «скачок-разрежение»

Для решения ряда практических задач используют приближенные методы расчета несимметричного обтекания тел вращения. Одним из них является метод, сочетающий в себе расчет конических течений и плоских течений, происходящих с расширением. Этот метод расчета часто называют методом " скачок-разрежение " (рис. 24). В приложении к несимметричному потоку около конус-цилиндрического тела этот метод состоит в том, что скорость течения и другие параметры в каждой плоскости конуса берутся из задачи об обтекании конуса под углом атаки. Эта задача может быть решена с помощью метода местных конусов. Коэффициент давления на поверхности конуса 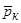и абсолютное значение давления можно рассчитать с помощью формулы (3.12) или графической зависимости рис. 4 прил. В случае несимметричного обтекания в качестве 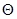берется угол местного конуса , рассчитываемый по формуле (3.14) или (3.17). Для определения угла наклона конического скачка уплотнения и безразмерной скорости 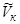на поверхности конуса можно воспользоваться графическими зависимостями рис. 3 и 5 прил.

Для расчета числа Маха на поверхности конуса М _к можно воспользоваться выражением вида (3.9):

,

а параметры на поверхности конуса ( и ) при необходимости рассчитываются по формулам для изоэнтропического течения.

Поток за угловой точкой тела (местом стыка конуса с цилиндром) рассчитывается как течение разрежения, известное под названием течения Прандтля-Майера, то есть как двумерный сверхзвуковой поток. Поворачивая вокруг угловой точки, поток газа ускоряется. Скорость течения на поверхности цилиндра зависит от угла разворота потока 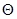. Для конус-цилиндрического тела 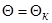. Чтобы осуществить расчет такого течения, надо воспользоваться графическими, табличными или аналитическими зависимостями для характеристик двумерного течения. Аналитические зависимости, описывающие течение Прандтля-Майера, достаточно громоздки, и вести расчет непосредственно по ним нерационально ввиду больших затрат времени (при ручном счете). Поэтому чаще всего при расчетах используют номограммы или таблицы, содержащие данные о параметрах потока в зависимости от угла поворота .

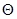При расширении звукового потока ( = 1) и возрастании скорости до значения поток должен развернуться на угол 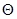. В случае > 1 для достижения того же значения числа угол разворота потока, естественно, должен быть меньше 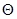. Табличные данные рассчитаны для значения скорости потока в начале разворота, равной скорости звука, т. е. для = 1. В случае конус-цилиндрического тела при полностью сверхзвуковом обтекании число Маха на поверхности конуса перед разворотом потока вокруг угловой точки = > 1. Поэтому для расчета течения расширения с помощью таблиц вначале пересчитывают угол разворота потока. Для этого, пользуясь той же таблицей, необходимо найти фиктивный угол .

Фиктивный угол поворота потока представляет собой угол поворота звукового потока () до получения заданного значения числа Маха > 1.

Рис. 25. Фиктивный угол поворота потока

В нашем случае = .Тогда суммарный угол поворота звукового потока очевидно равен (рис. 25) 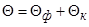. По величине этого угла 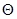по таблице можно найти значения всех параметров в конце разворота ( = , , …). Абсолютную величину давления рассчитывают следующим образом. Запишем отношение и преобразуем его:

, отсюда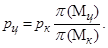

Здесь – газодинамическая функция, представляющая собой отношение давлений . Значения и можно определить из этих же таблиц по числам и . Таблицы для расчета сверхзвуковых течений газа с непрерывным увеличением скорости приведены в приложении.

Дата добавления: 2014-12-26