Общие сведения. Сопротивление тела вращения при сверхзвуковых скоростях

Сопротивление тела вращения при сверхзвуковых скоростях.

Тела вращения в сверхзвуковом потоке

Воздействие среды на движущееся в ней тело сводится к силам, непрерывно распределенным по всей поверхности тела. Эти поверхностные аэродинамические силы можно охарактеризовать величинами нормального p и касательного t напряжений в каждой точке поверхности тела. Распределенные по поверхности аэродинамические силы могут быть приведены к равнодействующей силе и паре сил с моментом .

При вычислениях и в экспериментальных исследованиях обычно приходится иметь дело не с векторами и , а с их составляющими в той или иной системе координат. Чаще всего используются скоростная и связанная системы координат (подробнее о системах координат см. книгу [2]). При осесимметричном обтекании тела потоком газа или, что тоже, при полете с нулевыми углами атаки и скольжения обе эти системы координат совпадают. Осесимметричным называют течение, обладающее симметрией относительно оси тела. Далее будем рассматривать только случай движения тела с нулевыми углами атаки.

В отличие от крыла, предназначенного для создания подъемной силы, фюзеляж летательного аппарата (ЛА) при небольших летных углах атаки почти не создает подъемной силы и при заданных размерах должен обеспечивать минимум лобового сопротивления.

Бескрылые ЛА обычно представляют собой длинное тонкое тело вращения, состоящее из заостренной или притупленной носовой части, корпуса – обычно цилиндрической формы, и сужающейся, цилиндрической или расширяющейся хвостовой (кормовой) части.

Лобовое сопротивление ЛА определяется по общей формуле аэродинамической силы:

, (3.1)

где – коэффициент лобового сопротивления, отнесенный к миделю аппарата , – скоростной напор набегающего потока.

При известном распределении нормальных и касательных напряжений по поверхности ЛА формула для расчета силы лобового сопротивления может быть представлена в виде

, (3.2)

где 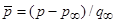– коэффициент давления; – местный коэффициент трения. Интеграл в выражении (3.2) – безразмерная величина, являющаяся, как следует из сопоставления формул (3.1) и (3.2), коэффициентом лобового сопротивления . Последняя формула позволяет выяснить, от каких параметров зависит коэффициент сопротивления. Для тела заданной формы и зависят от направления осей скоростной системы координат, то есть от углов атаки 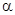и скольжения ; 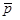и зависят от числа Рейнольдса Re, числа Маха и других критериев динамического подобия:

.

При осесимметричном обтекании тела для его цилиндрической поверхности , следовательно, сопротивление давления (сопротивление от сил нормального давления р) создается только теми частями тела, образующая контура которых не параллельна оси Ox: головной и кормовой (не цилиндрической формы) частями тела.

Как следует из формулы (3.2), коэффициент лобового сопротивления можно представить в виде суммы слагаемых

,

где 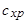и – коэффициенты сопротивления давления и трения соответственно. На величину коэффициента сопротивления трения влияет площадь боковой поверхности тела, которая зависит от удлинения ЛА. Удлинение – отношение длины корпуса ЛА к диаметру его миделя : .

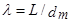С увеличением удлинения тела увеличивается поверхность трения, то есть возрастает сила сопротивления трения. Для тела, представляющего собой изолированный конус, сопротивление трения в диапазоне трансзвуковых и сверхзвуковых скоростей составляет всего несколько процентов от общего сопротивления.

Сопротивление давления создается осевой составляющей силы нормального давления p и для удобства расчета расчленяется на две части, одна из которых зависит от распределения давления по поверхности головной части тела, другая – от разрежения в донной области тела (за срезом кормовой части):

.

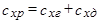Разрежение в донной области создает наружный поток, который стекает с поверхности кормовой части тела и эжектирует (отсасывает) воздух, находящийся в застойной области за дном. Чем больше разрежение в донной области, то есть чем больше разность между давлениями p_д в донной области и в невозмущенном набегающем потоке, тем больше величина .

На головной части тела статическое давление может существенно отличаться от его величины в окружающем внешнем потоке, что и является причиной возникновения составляющей . Скорость течения газа у поверхности тела в разных его точках неодинакова. В одних местах поток газа разгоняется: скорость его движения становится больше скорости набегающего потока, в других – подтормаживается. При больших дозвуковых скоростях полета местная скорость течения в некоторых точках тела достигает сначала скорости звука, а затем становится больше звуковой. Так, в поле дозвуковых скоростей на поверхности тела возникает местная сверхзвуковая зона, ниже которой течение также дозвуковое. Переход от сверхзвуковой скорости к дозвуковой происходит при ударном торможении сверхзвукового потока в скачке уплотнения, замыкающем зону местных сверхзвуковых скоростей. При сверхзвуковых скоростях набегающего потока скачок уплотнения образуется перед головной частью ЛА. Перед головной частью, имеющей форму заостренного конуса, при определенных условиях образуется конический скачок уплотнения, вершина которого находится в вершине конуса.

С возникновением скачков уплотнения кинетическая энергия потока расходуется на образование ударных волн, в которых происходят необратимые потери механической энергии потока (часть ее переходит в тепловую). Статическое давление за скачком уплотнения резко возрастает, что приводит к увеличению давления на поверхности головной части тела и к возрастанию коэффициента сопротивления давления. Это приводит к значительному возрастанию сопротивления тела.

Лобовое сопротивление, обусловленное потерями механической энергии (полного давления) в скачках уплотнения, называется волновым сопротивлением.

Таким образом, при сверхзвуковых скоростях потока полное сопротивление тела вращения можно представить в виде суммы трех слагаемых

,

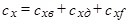где – коэффициент волнового сопротивления.

Как следует из формулы (3.2), коэффициент сопротивления головной части тела, за счет только нормальных напряжений, равен

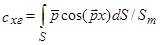. (3.3)

При сверхзвуковом обтекании заостренного конуса с присоединенным коническим скачком уплотнения статическое давление на всей поверхности конуса одинаково 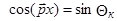, где 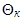– угол полураствора конуса. Тогда выражение (3.3) для сопротивления головной части существенно упрощается:

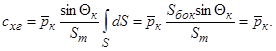
Таким образом, без учета донного сопротивления 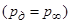коэффициент сопротивления давления отдельно взятого конуса при сверхзвуковых скоростях полета – коэффициент волнового сопротивления, – равен коэффициенту давления на поверхности конуса:

.

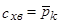Напомним некоторые сведения из теории скачков уплотнения. В частности, статическое давление за скачком уплотнения возрастает тем сильнее, чем выше потери механической энергии (полного давления) на скачке, т. е. чем больше угол b наклона скачка уплотнения. С увеличением скорости набегающего потока и уменьшением угла раствора конуса угол b уменьшается.

1.3.2. Расчет осесимметричного обтекания конуса назад

Дата добавления: 2014-12-26