Скорость истечения и расход газа при истечении из сопла

Рассмотрим истечение газа через сверхзвуковое сопло из достаточно большого резервуара, в котором скорость V ₀ может быть принята равной нулю, а давление, плотность и температура равны соответствующим значениям этих параметров при полном торможении.

Определим прежде всего скорость истечения из сопла, т. е. скорость в выходном сечении АА ₁ (рис. 9). Напишем уравнение Бернулли для двух сечений, одно из которых взято в резервуаре, второе является выходным сечением:

.

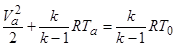Так как при изоэнтропическом истечении 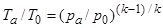, то формула для расчета скорости истечения принимает вид

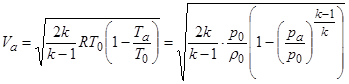. (2.8)

Здесь р_a и Т_a – давление и температура в выходном сечении сопла, равные, соответственно, при дозвуковом истечении внешнему давлению р_н и температуре Т _н окружающей среды.

Из формулы (2.8) видно, что скорость истечения тем больше, чем больше температура в резервуаре Т ₀ и чем меньше отношение давления на выходе к давлению торможения. При р_a / p ₀ = 1 истечения нет; при р_a / p ₀ = 0 скорость истечения равна

.

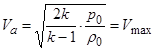Расход газа, который во всех сечениях сопла один и тот же, выразим следующим образом:

.

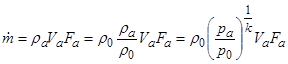Заменяя V_a по формуле (2.8), получим

.

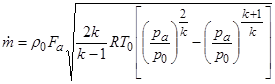С уменьшением относительного давления на выходе р_a / p ₀расход увеличивается, достигая максимума при

.

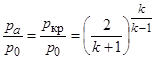При дальнейшем уменьшении р_a / p ₀скорость V_a становится сверхзвуковой. В этом случае относительное давление р_a / p ₀перестает влиять на расход.

Действительно, по уравнению постоянства расхода можно написать ,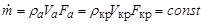

где 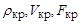– плотность, скорость и площадь сечения в критическом сечении сопла. При сверхзвуковом истечении скорость в этом сечении становится равной критической:

,

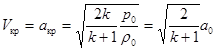т. е. постоянной величине, зависящей только от состояния газа в резервуаре, и остается ею, как бы ни изменялось давление вне сопла. Расход в этом случае будет равен

.

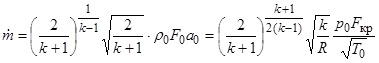Если принять k = 1.405, R = 287,3 (Дж/кг/К), то имеем

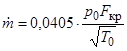(кг/с).

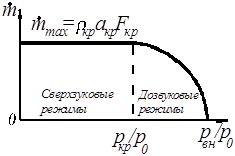Рис. 11. Зависимость расхода газа от относительного давления.

Таким образом, 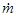зависит только от состояния газа в резервуаре (р ₀, Т ₀) и от площади критического сечения сопла 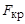. Зависимость расхода от относительного давления р _н / р ₀ показана на рис. 11.

Независимость расхода 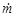от внешнего давления р _н/ р ₀ при сверхзвуковом истечении из сопла физически объясняется тем, что изменение внешнего давления р _н распространяется как всякое возмущение со скоростью звука, в то же время скорость V_а на срезе в данном случае больше скорости звука. Поэтому возмущения не в состоянии посредством волны распространяться внутри сопла: они все сносятся потоком наружу. В силу этого обстоятельства давление на выходе р_а только при дозвуковой скорости истечения будет равно внешнему давлению р _н.

При сверхзвуковом истечении р_а должно быть независимо от р _н (хотя, в действительности, в силу нарушения изоэнтропичности истечения р _н оказывает определенное влияние на р_а и при сверхзвуковом истечении), и связано с площадью выходного сечения F_а определенной зависимостью.

1.2.5. Относительная площадь сечения сопла и ее связь назад

Дата добавления: 2014-12-26