И статического давлений

Определение числа Маха путем измерения полного

У тупоносых тел в сверхзвуковом потоке на некотором расстоянии впереди тела образуется головная ударная волна (рис. 1). Наличие ударной волны меняет величину давления в критической точке тела.

Центральную часть ударной волны, расположенную непосредственно перед критической точкой K, можно считать прямым скачком уплотнения. Статические давления p ₁и p ₂ связаны условием перехода через прямой скачок уплотнения:

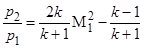. (1.4)

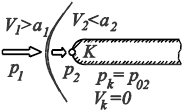Рис. 1. Обтекание тупоносого тела сверхзвуковым потоком

После того как поток пройдет через прямой скачок, скорость его V ₂ станет дозвуковой и далее будет адиабатически уменьшаться вплоть до точки K, где V_k = 0. Давление p_k = p ₀₂ в этой точке можно связать с давлением p ₂и скоростью за скачком формулой изоэнтропического течения:

,

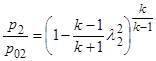где l ₂ = V ₂ / а _кp – приведенная скорость за скачком уплотнения. Так как для прямого скачка 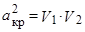и 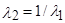, то последнее выражение можно переписать так:

.

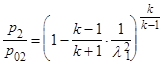Заменяя в этой формуле l ₁ его выражением через M₁, по формуле

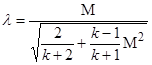, (1.5)

получим другую формулу связи p ₂ и p ₀₂:

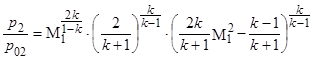. (1.6)

Разделив (1.4) на (1.6), свяжем давление в критической точке за ударной волной p ₀₂ с давлением в невозмущенном потоке перед ударной волной p ₁:

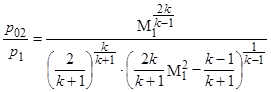. (1.7)

Пользуясь формулой Рэлея (1.7), можно, измерив давление в критической точке p_k = p ₀₂ и статическое давление перед ударной волной p ₁, определить число M₁.

Формулу Рэлея можно уверенно применять лишь в том случае, если переднее отверстие насадка целиком находится в зоне за прямым скачком уплотнения. Поэтому насадок для измерения полного давления p ₀₂ должен иметь затупленную головку.

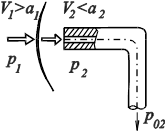Рис. 2. Насадок для измерения полного давления в сверхзвуковом потоке

С другой стороны, при затупленной форме головки насадка возникают существенные погрешности в измерении статического давления p ₁. Это обстоятельство препятствует применению приемника воздушного давления (ПВД), который используется для измерения полного и статического давления в дозвуковом потоке. Поэтому в сверхзвуковом потоке полное и статическое давления обычно измеряют отдельными насадками. Для измерения полного давления p ₀₂ применяются насадки в виде цилиндрической трубки с отверстием, обращенным против потока (рис. 2). Для того чтобы точнее измерять полное давление, приемное отверстие насадка делают значительно меньше, чем его наружный диаметр, с тем чтобы отверстие полностью находилось за прямым скачком.

При измерении статического давления p ₁ в сверхзвуковом потоке для ослабления интенсивности скачков уплотнения следует применять специальные насадки с остроконечной конической или оживальной головкой (рис. 3, а, б). Приемные отверстия, ось которых перпендикулярна направлению невозмущенного потока, должны располагаться на значительном расстоянии от начала цилиндрической части.

Кроме того, для измерения статического давления при сверхзвуковых скоростях может служить насадок в виде полуклина (рис. 3, в). Приемное отверстие располагается с плоской стороны насадка и статическое давление p₁ определяется не за скачком, а за волной возмущения, где изменения давления незначительны и ими можно пренебречь.

При одном и том же числе Маха давление в точке торможения p ₀₂, подсчитанное по формуле Рэлея (1.6), будет меньше того давления торможения p ₀₁, которое получается по формуле (1.3), выведенной для изоэнтропического торможения газа при отсутствии ударной волны.

Причина этого состоит в том, что сжатие газа в ударной волне сопровождается необратимым переходом части его механической энергии в тепловую. Эта часть энергии газа в дальнейшем уже не может быть вновь превращена в механическую и теряется безвозвратно, постепенно рассеиваясь в окружающем пространстве. Это и означает возрастание энтропии с физической точки зрения. Потери механической энергии в скачке характеризуются коэффициентом восстановления полного давления s, представляющим собой отношение давлений торможения p ₀₂ /p ₀₁ за и перед скачком уплотнения. В случае прямого скачка этот коэффициент может быть определен по следующей формуле:

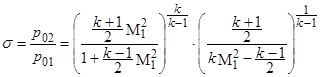. (1.8)

Зависимость (1.8) позволяет определить число M₁ потока по замеренным значениям p ₀₂и p ₀₁. В силу того, что течение до скачка уплотнения может считаться изоэнтропическим, давление p ₀₁ принимается равным давлению торможения в форкамере АДТ. На рис. 1 прил. показаны зависимости отношений давлений торможения до и после скачка и давления торможения за скачком к статическому давлению в функции от числа M₁ перед скачком.

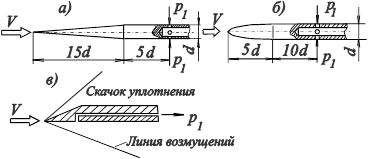Рис. 3. Насадки для измерения статического давления в сверхзвуковом потоке

Таким образом, для определения числа Маха одним из измеряемых давлений является полное давление в форкамере АДТ. Вторым измеряемым давлением может быть статическое давление или полное давление за прямым скачком. Для определения числа Маха дозвукового потока обычно измеряют статическое давление. Измерениями статического давления в рабочей части АДТ целесообразно пользоваться до чисел M = 1.6...1.8. При больших числах Mахастатическое давление в рабочей части быстро падает, и точность определения M резко уменьшается. Определение числа M по измерениям полного давления за прямым скачком p ₀₂ при скоростях, незначительно превышающих скорость звука, недостаточно точно из-за того, что давление p ₀₂ мало отличается от p ₀₁. Но с возрастанием числа M потери в скачке растут, и уже при M > 1,8 использование p ₀₂ дает достаточную точность в определении числа Маха.

1.1.2. Определение числа Mаха потока оптическим методом назад

Оптические методы исследования основаны на связи плотности движущейся среды с ее оптическими свойствами. Три важнейших оптических метода: теневой, шлирен-метод и интерферометрический – основаны на том, что скорость света зависит от плотности той среды, через которую проходят его лучи. Коэффициент преломления n, равный отношению скорости света c в некоторой среде к скорости света c ₀ в пустоте (n = c/c ₀), зависит от плотности среды:

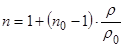, (1.9)

где n ₀ и r ₀ соответственно начальные значения коэффициента преломления и плотности газа.

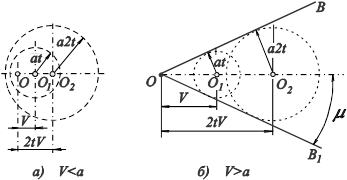Рис. 4. Образование волн слабого возмущения при различной скорости движения тела

Из формулы (1.9) видно, что в среде с изменяющейся плотностью показатель преломления также переменный. Это приводит к тому, что при прохождении световых лучей через такую среду происходит, во-первых, поворот волнового фронта и, во-вторых, сдвиг фазы, различный на различных лучах. Первый эффект используется в теневом и шлирен-методах, второй положен в основу интерферометрического метода.

Возмущенное течение газа в рабочей части АДТ представляет собой оптически неоднородный поток, характеризуемый изменением плотности и коэффициента преломления.

Рассмотрим характер обтекания точечного источника возмущений потоком газа. Волны возмущения, вызванные таким источником, являются волнами сферического типа очень малой интенсивности. Они распространяются со скоростью звука а, образуя семейство сфер с радиусом от нуля до аt на рассматриваемом отрезке времени. При движении точечного источника возмущений со скоростью V < а сферические волны смещаются в сторону источника, но опережают его, т.е. источник находится внутри сферической волны, вызванной этим телом (рис. 4, а). В случае же когда скорость источника возмущений оказывается больше скорости распространения волны (V > a), тело обгоняет волны, оставляя их позади себя в виде расширяющегося конуса, вершиной которого оно является (рис. 4, б).

Этот конус является огибающей сферических волн возмущений и называется конусом возмущения или конусом Маха. Если этот конус рассечь плоскостью, проходящей через его ось, то мы получим прямые OB и OB ₁, называемые линиями возмущений (линиями Маха), которые являются ударными волнами бесконечно малой интенсивности. Угол , равный половине угла при вершине конуса, называется углом возмущений. Этот угол связан со скоростью движения тела и скоростью звука зависимостью , откуда

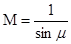. (1.10)

При = p/2 sin =1 и M = 1, т. е. V = а (скорость источника равна скорости звука). Из уравнения (1.10) видно, что с уменьшением угла увеличивается число Маха.

Таким образом, зарисовывая или фотографируя линии возмущения, можно установить число Маха потока. Для этого с необходимой точностью измеряется угол m, а затем вычисляется число M по формуле (1.10). Отметим, что точность определения числа M по углу невелика.

Если возмущения, вносимые в поток телом, становятся большими, что наблюдается при конечных размерах тела, то перед телом образуется скачок уплотнения.

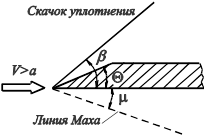Рис. 5. Обтекание клина сверхзвуковым потоком газа

Более точно числоM определяется по углу наклона ударной волны на клине или конусе, вершина которого помещается в исследуемую точку потока, а ось совмещается с направлением вектора скорости. Если угол при вершине Q не превышает некоторого предельного значения, то обтекание характеризуется возникновением перед телом прямолинейного присоединенного скачка уплотнения, наклоненного под углом b к вектору скорости V (рис. 5). В этом случае для определения числа M используют известную зависимость между числом M, углом наклона ударной волны b и углом раскрытия конуса или клина Q. Для клина эта зависимость выражается уравнением

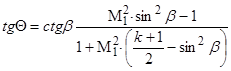. (1.11)

График зависимости (1.11) представлен на рис. 2 прил.

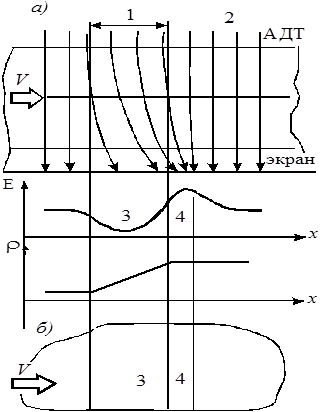Рис. 6. Визуализация скачка уплотнения: а- схема метода; б – теневое изображение скачка уплотнения; (1 – граница скачка уплотнения, 2 – сверхзвуковой поток, 3 – зона пониженной освещенности, 4 – зона повышенной освещенности)

При помощи оптических методов исследования можно сфотографировать поток около клина и получить теневой снимок, на котором будет изображена линия скачка уплотнения. Оптические методы не дают возможности увидеть линии Маха, вместо них наблюдают ударные волны очень малой, но конечной интенсивности, образуемые, например, царапинами на твердой стенке или острой кромке. Вычисленное по углу слабых возмущений значение числа Маха несколько меньше его действительной величины, так как скорость распространения наблюдаемых слабых волн несколько превышает скорость звука и их огибающая будет наклонена к направлению скорости под углом несколько большим, чем .

Для наблюдения скачков уплотнения применяется теневой метод. На рис. 6 схематично показано теневое изображение скачка уплотнения и поясняются физические основы метода. Рабочая часть АДТ просвечивается параллельным световым пучком. Если плотность среды постоянна, то световые лучи, пройдя рабочую часть, равномерно освещают экран. Скачок уплотнения вносит оптическую неоднородность в поле течения. Это связано с тем, что плотность изменяется вдоль оси АДТ. Световые лучи отклоняются от первоначального направления, вызывая неравномерную освещенность E экрана. Причем в пределах скачка уплотнения освещенность существенно ниже, чем за скачком. Изображение скачка уплотнения представляет собой темную полосу со стороны набегающего потока, ограниченную яркой каймой, освещенность которой постепенно уменьшается.

Основным недостатком теневого метода является то, что хотя изменение освещенности экрана зависит от плотности среды, получить количественные данные о распределении плотности оказывается весьма трудно. Причина этого состоит в том, что световые лучи от различных точек потока, преломившись, могут попасть на одно и то же место экрана. Поэтому на практике для визуального определения плотности и давления в потоке газа применяют шлирен-метод или интерферометрический метод.

Шлирен-метод состоит в измерении смещения светового луча, проходящего через оптически неоднородную среду. В случае плоского потока это смещение пропорционально градиенту плотности.

Интерферометрический метод основан на разделении монохроматического луча света на два когерентных луча (опорный и рабочий), которые после прохождения заданного пути вновь соединяются и дают интерференционные эффекты. При прохождении световых пучков через среду с постоянной плотностью интерференционные полосы будут параллельны друг другу. Если на пути одного из пучков света окажется среда с другим коэффициентом преломления, то произойдет сдвиг полос; если при этом имеются градиенты плотности, то полосы к тому же и деформируются. По сдвигу и деформации полос определяют плотность газа.

Основными преимуществами оптических методов являются безынерционность и отсутствие необходимости вводить в поток возмущающие его механические приспособления.

Дата добавления: 2014-12-26