И сечением струйки тока

Сопло Лаваля

1.2.1. Зависимость между скоростью течения газа назад

При движении несжимаемой жидкости скорость потока изменяется обратно пропорционально площади поперечного сечения согласно уравнению неразрывности:

.

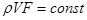В случае движения сжимаемой жидкости (газа) это уравнение приводит к другим выводам. Как показано в п. 1.1, уравнение неразрывности в дифференциальной форме может быть сведено к виду

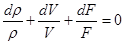. (1.11)

Соотношение (1.2) 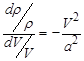показывает, что при V < a относительное изменение плотности dp / r меньше, чем относительное изменение скорости dV/V, а при сверхзвуковых скоростях (V > а) наоборот: плотность изменяется быстрее, чем скорость.

Подставив (1.2) в (1.11), получим:

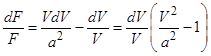(1.12)

Уравнение (1.12) показывает, что связь между скоростью течения газа V и площадью поперечного сечения F имеет разный характер в зависимости от того, будет ли скорость течения больше или меньше скорости звука а.

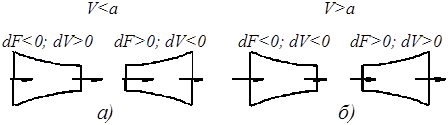Рис. 7. Изменение скорости вдоль потока в дозвуковом (а) и сверхзвуковом (б) потоках

Если V < а, то величина, стоящая в скобках правой части уравнения (1.12), будет отрицательной, и знаки dF и dV будут, следовательно, разными. Это значит, что в дозвуковом потоке газа скорость меняется так же, как и в потоке несжимаемой жидкости, т. е. с увеличением площади поперечного сечения F скорость V убывает и наоборот (рис. 7, а).

Если же V > а, то знак dF совпадает со знаком dV, иначе говоря, с увеличением F скорость V также увеличивается, а с уменьшением F - уменьшается (рис. 7, б). Такое явление в газе возможно потому, что увеличение скорости здесь сопряжено не только с понижением давления, как в несжимаемой жидкости, но и с разрежением, т.е. с уменьшением плотности. Расширение струек газа в сверхзвуковом течении ведет к расширению самого газа (в термодинамическом смысле), то есть к уменьшению давления, плотности и температуры и к увеличению скорости.

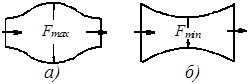Рис. 8. Изменение сечения потока, исключающее (а) и обеспечивающее (б) достижение скорости звука

При V = а dF = 0. При непрерывно изменяющейся скорости (т. е. при 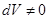) это может быть только в экстремальном, а именно в минимальном сечении потока. Действительно, если бы на входе расширяющейся части потока (рис. 8, а) скорость была бы меньше скорости звука а, то, согласно изложенному выше, она уменьшалась бы вдоль направления течения. В противном случае если бы на входе V было больше а, то она бы увеличивалась. В обоих случаях при переходе через 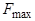скорость течения никак не может сравняться со скоростью звука.

Наоборот, в сужающемся участке потока (рис. 8, б) дозвуковая скорость будет увеличиваться, а сверхзвуковая – уменьшаться, и в обоих случаях достижение скорости звука возможно. Сечение потока, в котором скорость течения V достигает скорости звука а, называют критическим.

Эту особенность газовых струй учитывают при проектировании специальных насадков (сопел), которые должны обеспечивать истечение газа со сверхзвуковой скоростью.

1.2.2. Сверхзвуковое сопло назад

Сверхзвуковое сопло, называемое соплом Лаваля, имеет форму насадка, вначале сужающегося для того, чтобы увеличить скорость от V ₀ = 0 (внутри резервуара), до V = а (в наиболее узком сечении), затем расширяющегося с тем, чтобы обеспечить дальнейшее нарастание сверхзвуковой скорости. Схема сверхзвукового сопла показана на рис. 9 сверху. Ниже на том же рисунке схематически изображены кривые изоэнтропического изменения скорости и давления вдоль оси сопла, соответствующие четырем различным случаям течения газа (линии I – IV).

Рис. 9. Изменение давления и скорости вдоль оси сопла, соответствующее четырем различным случаям течения газа

Если поток газа, протекающий сквозь сопло Лаваля, имеет везде скорость меньше скорости звука, то изменение скорости и давления вдоль сопла происходит по кривой I (рис. 9). Во входной части скорость нарастает, в сжатом сечении достигает максимума и в выходной части убывает. Давление нигде не достигает критического значения (p _кр = 0,5283 p ₀ для воздуха и других двухатомных газов), и сопло, по существу, ничем не отличается от трубки Вентури.

Если поток газа имеет везде сверхзвуковую скорость, то изменения скорости и давления вдоль сопла происходят по кривой II. Во входной части скорость уменьшается, в сжатом сечении достигает минимума и затем в выходной части нарастает. В этом случае давление также нигде не достигает значения p _кр.

Кривые III и IV (рис. 9) показывают изменения скорости и давления при переходе через скорость звука а _кр, которая имеет место в наиболее узком сечении сопла. Кривые III характеризуют разгон газа от дозвуковых до сверхзвуковых скоростей; кривая IV, наоборот, – изоэнтропическое торможение газа от сверхзвуковых к дозвуковым скоростям. Типичными для сверхзвуковых сопел являются кривые III, так как эти сопла предназначаются для разгона газа до сверхзвуковых скоростей.

Кривые I – IV имеют только теоретическое значение, так как в действительности в соплах всегда имеется трение, а также (в сверхзвуковой части сопла) скачки уплотнения, которые нарушают изоэнтропический характер течения.

1.2.3. Изменение параметров газа в изоэнтропическом течении назад

Дата добавления: 2014-12-26