С относительными скоростью и давлением

Связь между давлением и площадью сечения сопла при изоэнтропическом истечении можно установить с помощью уравнения постоянства расхода следующим образом. Из уравнения неразрывности , используя формулу (2.7), находим

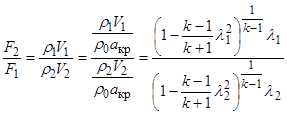. (2.9)

Отсюда видно, что отношение площадей в двух разных произвольных сечениях сопла зависит только от рода газа и от относительных скоростей l ₁ и l ₂ в этих сечениях.

Введем относительную площадь сечения сопла f = F/F _кр. Тогда по формуле (2.9), полагая F ₂ = F, F ₁ = F _кр, l ₂ = l и l ₁ = 1, получим

. (2.10)

Приведенную скорость l можно заменить через относительное давление, воспользовавшись формулой (2.6):

.

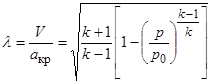Тогда

.

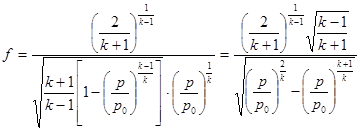Видим, что если сопло задано, т. е. величина f в каждом сечении конструктивно определена заранее, то относительное давление р/р ₀ (а также относительные температура Т/Т ₀ и плотность r/r ₀) в каждом сечении являются вполне определенными величинами.

В случае дозвукового истечения изменение внешнего давления, передаваясь вдоль струи внутрь сопла, будет оказывать влияние на величину р и р ₀; отношение р/р ₀ при этом изменяться не будет. При сверхзвуковом истечении как местное давление р, так и р ₀ вообще не зависят от внешнего давления.

Воспользовавшись зависимостью (1.5) между относительной скоростью l и числом Маха, выражение (2.10) можно преобразовать в следующее:

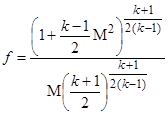. (2.11)

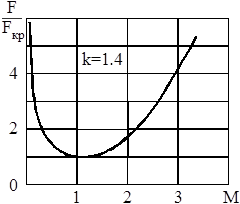Рис. 12. Зависимость безразмерной площади сверхзвукового сопла от числа Маха

При k = 1,4 эта формула принимает вид

.

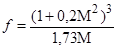График зависимости f от числа М, построенный по этой формуле, показан на рис. 12. Как видим, одно и то же значение f соответствует двум разным числам М, одно из которых меньше единицы, другое – больше, как этого и следовало ожидать, исходя из того, что в дозвуковой части сопло должно сужаться, а в сверхзвуковой – расширяться.

Формула (2.11) показывает, что при выбранных форме и размерах сопла число М, которое получается в любом его сечении, в том числе и в выходном, будет заранее определено и не зависит ни от внешних условий (p _н, T _н), ни от условий в резервуаре (p ₀, T ₀). Для получения на выходе из сопла определенного значения числа М необходимо соответствующим образом подобрать площадь сечения и, кроме того, надо иметь достаточный запас давления в резервуаре.

1.2.6. Режимы работы сверхзвукового сопла назад

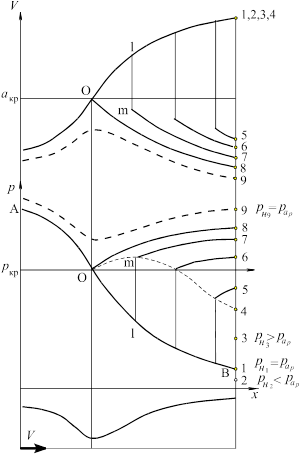Рис. 13. Распределение давления и скорости в сверхзвуковом потоке при различных режимах работы сопла

Характер распределения параметров течения газа в сопле зависит от степени нерасчётности струи n, равной отношению давления на выходе из сопла р_a к давлению окружающей среды р _н (n = р_а / р _н). В зависимости от величины нерасчётности n сверхзвуковое сопло может работать на режимах: расчетном, недорасширения и перерасширения. Истечение через сопло при разных давлениях внешней среды схематично показано на рис. 13.

1. Расчетный режим – давление на срезе сопла равно давлению окружающей среды р_а = р _н (n = 1). Изменение скорости и давления газа в сопле изображено линиями АОВ. За соплом сверхзвуковая струя сечением F_а течет со скоростью V_а при давлении р_а = р _н. По мере удаления от сопла скорость газа уменьшается за счет турбулентного смешивания с окружающим газом.

2. Режим недорасширения – давление на срезе сопла больше давления окружающей среды р_а > р _н (n > 1). Характер изменения скорости и давления газа в тракте сопла на режиме недорасширения совпадает с расчетным (линия АОВ), давление на срезе сопла и скорость истечения остаются расчетными. Волны пониженного давления из окружающей среды не могут достичь среза сопла – они сносятся сверхзвуковым потоком. Избыточное давление (р_a – р _н2) расходуется на увеличение скорости сверхзвукового потока, но уже за срезом сопла.

3. Режим перерасширения – давление на срезе сопла меньше давления окружающей среды: р_а < р _н (n < 1). До некоторого предела повышение давления окружающей среды р _н4 (рис. 13) не влияет на течение по соплу, которое остается расчетным (линия АОВ от точки 1 до точки 4). Волны повышенного давления сносятся сверхзвуковым потоком, истекающим из сопла. Эта схема истечения возможна лишь при небольшом превышении давления р _н над р_а. При значительном же противодавлении среды струи газа, вырывающиеся из сопла со сверхзвуковыми скоростями, встречая на своем пути массы малоподвижного газа, находящегося под более высоким давлением, испытывают газовый удар. Удар приводит к скачкообразному изменению параметров газа, истекающего из сопла, т. е. к появлению скачка уплотнения. Фронт скачка уплотнения в виде волны перемещается быстрее скорости звука, поэтому скачки, двигаясь против течения, входят внутрь сопла и при повышении давления до р _н8 проникают иногда вплоть до критического сечения. Такие глубоко проникающие в сопло скачки обычно прямые, поток за ними дозвуковой и давление меньше критического. Например, при р _н7 реализуется течение дозвуковое в сужающейся час ти сопла, сверхзвуковое на участке O l в расширяющейся части до ударной волны и дозвуковое на участке m7 за ударной волной. За скачком вниз по течению в расширяющейся части сопла дозвуковая скорость может только падать, а давление – возрастать. Наконец, при р _н8 скачок доходит до критического сечения и исчезает. При р _н9 устанавливается режим полностью дозвукового течения трубки Вентури. На режимах р _н4... р _н9 дозвукового истечения из сопла давление на срезе сопла равно давлению окружающей среды.

1.2.7. Структура струи назад

Сверхзвуковое сопло очень широко используют в реактивных двигателях. Струя газа, выходящего из сопла, сообщает двигателю реактивную силу (тягу), под действием которой осуществляется полет реактивного аппарата.

В реальных условиях параметры истекающего из сопла газа и картина течения в сверхзвуковой струе могут изменяться под воздействием различных причин (высоты полета, скорости движения аппарата и др.). При этом, как уже было сказано выше, различают три основных режима работы сопла, характеризуемых степенью нерасчётности струи n:

1) режим недорасширения, n > 1;

2) расчетный режим, n = 1;

3) режим перерасширения, n < 1.

При истечении газа в среду с пониженным давлением струя расширяется в окружающей среде с образованием конических волн разрежения, и давление падает от р_а до р_н (рис. 14, а). В ядре струи давление снижается до еще меньшего значения, возникает поперечный градиент давления. Это приводит к отклонению линий тока от оси и вызывает увеличение поперечного сечения струи. Волны разрежения, выходя на границу струи, отражаются от нее волнами сжатия, при прохождении через которые линии тока деформируются в противоположном направлении – струя сжимается. Характеристики, сходящиеся к оси струи, образуют криволинейный скачок уплотнения, который имеет форму поверхности вращения. При значительном отклонении режима от расчетного (р_а > р_н) "висячий" скачок ДВВ ₁ Д ₁ зарождается не у входной кромки сопла, а в ядре струи, на некотором расстоянии от ее границы. Интенсивность " висячего " скачка возрастает по мере удаления от среза сопла. При степени нерасчётности струи (n 2) возникает дискообразный скачок ВВ ₁, пересекающий ось струи под прямым углом.

С контура этого диска сходит тангенциальный разрыв ВQВ ₁ Q _1, отделяющий внутреннюю дозвуковую часть струи от внешней – сверхзвуковой. Во внешней сверхзвуковой области образуется криволинейный скачок CВВ ₁ C ₁, являющийся продолжением скачка ДВВ ₁ Д ₁. Таким образом (при n 2) за срезом сопла формируется мостообразный скачок ДВСС ₁ В ₁ Д ₁, природа которого связана с перерасширением сверхзвуковой струи. Струя суживается до того сечения, где скачок CВВ ₁ C ₁ выходит на границу струи и отражается в виде волны разрежения. Далее струя вновь расширяется, от границы отходят звуковые волны, пересекающиеся в ядре струи. В результате здесь образуется конический скачок ЕЕ ₁ FF ₁, замыкающий волну разрежения СЕЕ ₁ С ₁ и выходящий на поверхность струи в точках F и F ₁.

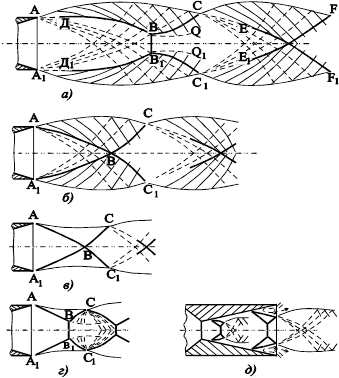Рис. 14. Структура сверхзвуковой струи при различных режимах работы сопла: недорасширении (а), расчетном (б), перерасширении (в, г), перерасширении с отрывом (д)

По мере повышения давления среды система скачков на выходе из сопла меняется мало, и при расчетном режиме (n = 1) за выходным сечением сохраняются два осесимметричных криволинейных скачка АВА ₁ и СВС ₁ (рис. 14, б). Внутренний прямой скачок и дозвуковое ядро отсутствуют.

При дальнейшем возрастании давления среды на режиме перерасширения (n < 1) форма границы струи меняется. Восстановление давления в струе происходит при помощи криволинейных скачков АВА ₁ и СВС ₁, сходящих с кромки сопла (рис. 14, в). При большом перерасширении в окрестности оси струи образуется прямой дискообразный скачок, за которым скорость становится дозвуковой (рис. 14, г). С контура этого диска сходит тангенциальный разрыв, и образуется еще один расходящийся конусообразный скачок СВВ ₁ С ₁, который, отражаясь от свободной границы в т. С и С ₁, вызывает появление центрированной волны разрежения. В результате этого начинается расширение струи, и течение можно рассматривать как течение с недорасширением.

Известно, что слабые возмущения в среде распространяются со скоростью звука и поэтому не могут проникнуть внутрь сопла навстречу потоку, текущему со сверхзвуковой скоростью, т. е. давление на выходе из сопла р_а не зависит от внешнего давления. Однако в действительности дело обстоит несколько иначе. Фронт скачка в виде волны перемещается быстрее скорости звука, причем скорость распространения ударной волны тем больше, чем сильнее скачок, т. е. чем больше разность давлений р_н – р_а. Поэтому при достаточном перепаде давления скачок оказывается в состоянии, двигаясь против течения, войти внутрь сопла (рис. 14, д) и проникнуть иногда даже вплоть до критического сечения, при этом он вырождается в слабую сверхзвуковую волну. Сопло в этом случае работает как обычный дозвуковой диффузор (рис. 15, кривая 4). Дальнейшее возрастание давления среды приводит к тому, что сопло начинает работать как трубка Вентури (рис. 15, кривая 5).

Форма расширяющейся части сопла оказывает значительное влияние на структуру струи за соплом. В правильно спрофилированном осесимметричном сопле скачки уплотнения за выходным сечением возникают только при больших отклонениях режима от расчетного. На расчетном режиме и при незначительных отклонениях от него сопло работает без скачков уплотнения на выходе.

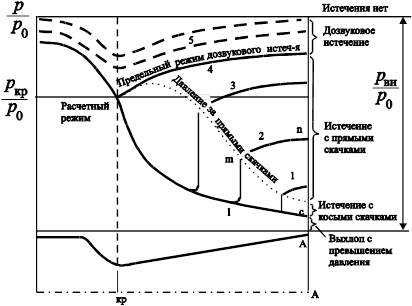Рис. 15. Распределение давления в сверхзвуковом сопле при различных режимах работы

В конических соплах скачки в струе обнаруживаются при всех режимах. С увеличением угла раствора расширяющейся части интенсивность скачков и их кривизна увеличиваются. Вместе с тем увеличение угла раствора оказывает значительное влияние на структуру потока в сопле при расчетном и нерасчётных режимах. По мере увеличения угла раствора растет величина отрицательного градиента давления в расширяющейся части, возрастает неравномерность потока по оси струи и в выходном сечении.

1.2.8. Распределение давления вдоль оси сопла назад

При движении внутри сопла скачок, взаимодействуя с пограничным слоем, вызывает отрыв потока по кольцевому сечению, и вследствие этого теоретически возможная степень расширения газа в сопле используется далеко не полностью. За скачком вниз по течению в расширяющейся части сопла дозвуковая скорость может только падать, а давление – возрастать. Причем полного восстановления давления не происходит в результате роста энтропии в скачке.

Это сказывается прежде всего в том, что статическое давление непосредственно за скачком р₂, будучи отнесено к давлению торможения р ₀₁, оказывается часто меньше, чем р _кр /р ₀₁. Причиной этого является уменьшение давления торможения при проходе газа через скачок. Если относительное давление р ₂ /р ₀₁ нанести на диаграмму вдоль оси сопла, то получится кривая, показанная пунктиром на рис. 15 (внизу, справа). Давление р ₂ / р ₀₁ вначале как бы стремится следовать вдоль кривой, соответствующей предельному режиму дозвукового истечения, при котором потерь энергии нет. Это объясняется тем, что вблизи критического сечения скачки еще очень слабые. Однако уже вскоре за критическим сечением кривая отходит от кривой дозвукового истечения и, пройдя максимум, круто устремляется вниз. Быстрое падение р ₂ /р ₀₁ за максимумом объясняется возрастающей силой газового удара соответственно возрастанию скорости потока вдоль оси сопла.

После того, как давление скачкообразно возрастет до величины р ₂ /р ₀₁ (участок 1 m, рис. 15), оно продолжает далее возрастать вдоль одной из кривых mn, соответствующих дозвуковому изоэнтропическому торможению до давления р_н /р ₀₁.

Если внешнее давление окажется достаточно низким (ниже точки с на рис. 15), но все же более высоким, чем давление на выходе р_а, то прямого скачка внутри сопла не образуется. В этом случае следует ожидать появления слабых косых скачков недалеко от выхода из сопла или в струе за выходным сечением.

1.2.9. Тяга сверхзвукового сопла назад

Тяга сопла является равнодействующей газодинамических сил, действующих на внутренние поверхности сопла при истечении из него газа и сил давления окружающей среды, действующих на его внешние поверхности. На внутреннюю поверхность сопла действует переменное давление, изменяющееся от давления в ресивере р ₀ до давления на срезе сопла р_а (рис. 16). На внешнюю поверхность действует давление окружающей среды p_н.

Согласно определению, тяга сопла равна ,

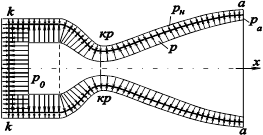Рис. 16. Распределение давления по поверхностям сопла

где n – нормаль к поверхности; х – ось сопла; S – полная (внутренняя и внешняя) поверхность сопла.

Для решения этого интеграла тягу можно разбить на четыре составляющие, причем составляющие, совпадающие с направлением вектора скорости истечения, принимаются положительными и наоборот:

–R = – R ₁ – R ₂ + R ₃ – R ₄,

где R ₁, R ₂, R ₃, R ₄ – равнодействующие сил давления, действующих на головку и боковую стенку ресивера, суживающуюся (докритическую) и расширяющуюся (закритическую) части сопла. При этом для сопла с цилиндрическим ресивером сила R ₂ равна нулю, так как радиальные составляющие сил давления, действующих на цилиндрическую стенку ресивера, взаимно уравновешиваются.

Для определения силы R₁ используем теорему импульсов для газа, действующего на контур головки ресивера. Согласно уравнению количества движения сумма проекций на ось х всех внешних сил, приложенных к этому контуру, равна проекции изменения секундного количества движения:

,

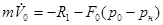где F ₀ – площадь сечения ресивера, V ₀ – скорость движения газа в ресивере. Откуда

.

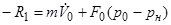Для определения силы R ₃ просуммируем осевые составляющие сил давления, действующих на суживающуюся часть сопла. Осевая проекция сил давления, действующих на кольцевой элемент сопла шириной dх,

,

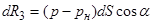где dS – поверхность элементарного конуса высотой dх, a – угол между положительными направлениями оси x и нормалью к поверхности.

Учитывая, что dScos 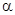есть проекция площадки dS на плоскость, перпендикулярную оси, т. е. dScos 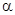= dF, сила dR ₃ = (p – p_н) dF. Интегрируя dR ₃ по всей поверхности рассматриваемого участка ресивера, получим

.

Интегрируя по частям pdF, найдем, что

.

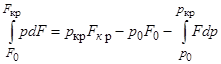Используя уравнение неразрывности F = 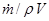и Бернулли VdV = – dp/p, а также учитывая, что 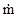= const, получим

.

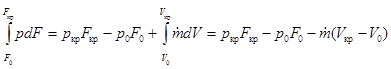Подставив значение интеграла в уравнение для силы R₃, найдем, что R ₃ = p _кр F _кр– p ₀ F ₀ + 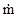(V _кр – V ₀ ) – p _н (F _кр – F ₀ ).

Сила R₄ получается аналогично:

.

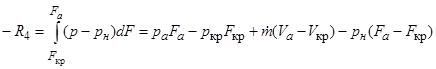Подставляя силы R ₁, … ,R ₄ в исходное уравнение, получим окончательную формулу для расчета тяги сопла:

R = 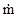V_a + F_a (p_a – p _н ). (2.11)

Знак "минус" в формуле тяги отсутствует, т. к. на практике обычно имеют дело с абсолютным значением тяги. Формула тяги получена суммированием сил давления, действующих на внешнюю и внутреннюю поверхности сопла:

.

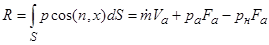Следовательно, этот интеграл можно разбить на два:

,

из которых первый характеризует тягу, создаваемую силами давления, приложенными к внутреннему контуру сопла, а второй – тягу, создаваемую силами давления окружающей среды, приложенными к внешнему контуру, т. е.

,

.

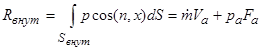Тяга, снимаемая с внешнего контура R_внеш, характеризует влияние только внешнего давления. Из (2.11) следует, что увеличить тягу можно за счет роста расхода газа 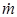и скорости его истечения V_а. Наибольшее значение тяги при заданных параметрах достигается в пустоте (р_н = 0). Когда отрицательная составляющая тяги р_нF_а = R_внеш равняется нулю, тяга

R_n = R_внут = 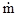V_a+p_aF_a.

Следовательно, тяга при каком-то давлении окружающей среды (при бесскачковом режиме работы сопла) связана с тягой R_внут соотношением

R = R_внут – p_н F_a.

Таким образом, тяга сопла на режимах недорасширения и перерасширения без отрыва пограничного слоя определяется по формуле

R = 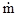V_a + F_a (p_a – p_н).

Учитывая, что 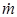= 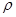V_aF и M _a = V_a/a, последнее уравнение можно привести к виду

R = F_a p_a (1 + k M ²_a) – F_a p_н,

где M _a – значение числа Маха на срезе сопла.

На расчетном режиме работы сопла, при котором давление на срезе сопла равно давлению окружающей среды, тяга определяется по зависимости

R_расч = V_a

или R_расч = F_a p_a k M ²_a.

Рис. 17. Схема работы сопла на режимах: недорасширения (а), расчетном (б) и перерасширения (в)

Большое влияние на величину тяги оказывает режим работы сопла. При заданном давлении в ресивере р ₀ можно назначить различные степени расширения газа в сопле, при которых давление на срезе сопла может быть больше, меньше или равно давлению окружающей среды. Из (2.11) сразу не видно, при какой степени расширения (при р_н = const, р ₀ = const, = const) достигается максимальное значение тяги сопла. Но это хорошо можно уяснить, рассматривая тягу сопла как результат действия сил давления на внешнюю и внутреннюю поверхности. На рис. 17 представлены эпюры распределения давления газа в сопле и давления окружающей среды, действующих на закритические части трех сопл. На рис. 17, а изображено сопло с недорасширением, т. е. р_а > р_н. При удлинении сопла до размеров, когда в выходном сече нии сопла р_а = р_н (рис. 17, б), тяга сопла увеличивается на некоторую величину + 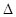R, так как силы давления газа, действующие на удлиненную часть сопла, везде больше сил давления окружающей среды.

В режиме перерасширения газа в сопле (рис. 17, в) его давление, начиная с сечения, где р_а = р_н, на стенке везде меньше давления окружающей среды. Поэтому проекция на ось x сил внешнего давления, действующих на стенку сопла, будет больше проекций сил давления, действующих на этот же участок сопла со стороны газа. В результате эта часть сопла дает отрицательную тягу 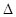R. Таким образом, как на режиме недорасширения, так и на режиме перерасширения тяга сопла меньше, чем на расчетном режиме.

Для получения наибольшего значения тяги необходимо проектировать сопло с расчетным режимом его работы. Однако подавляющее большинство сопл работает на нерасчётном режиме. В связи с этим важно количественно оценить потери в тяге на различных нерасчётных режимах работы сопла.

Рассмотрим, как изменяется тяга с изменением безразмерной площади выходного сечения сопла F_a /F _кр (давления на срезе сопла) при постоянном давлении в ресивере и в окружающей среде. На рис. 18 представлены результаты расчета тяги по формуле (2.11). Максимальное значение тяги соответствует расчетному режиму сопла, когда геометрия сопла обеспечивает расширение газов до давления окружающей среды.

Рис. 18. Зависимость тяги сопла от относительной площади (p₀ = const)

При уменьшении безразмерной площади сопла (увеличении давления на срезе сопла), например, в два раза, потери в тяге по отношению к расчетному режиму составляют 4%, а при увеличении в два раза тяга уменьшается на 0,5%. Следовательно, при работе сопла с недорасширением потери в тяге значительно больше, чем при работе сопла с перерасширением. Это можно объяснить, если рассматривать тягу сопла как результат действия сил давления на внешнюю и внутреннюю поверхности сопла.

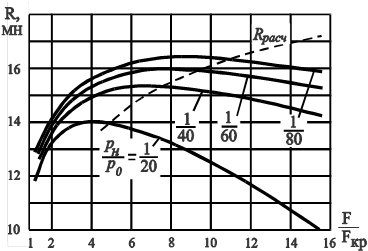Рис. 19. Зависимость тяги от относительной площади сопла и давления в ресивере (p_н = const)

На рис. 19 показано изменение тяги сопла в зависимости от давления в ресивере и безразмерной площади сопла при постоянном давлении окружающей среды. Чем больше давление в ресивере, тем более плавно изменяется тяга при отклонении режима работы сопла от расчетного и наоборот. Следовательно, потери тяги на нерасчетных режимах работы возрастают более интенсивно у сопла с меньшим давлением р ₀. Это объясняется тем, что с повышением давления в ресивере доля тяги, получаемая с внешней поверхности сопла, по сравнению с тягой, обеспечиваемой его внутренней поверхностью, уменьшается. В пределе, когда давление в ресивере стремится к бесконечности, величина тяги стремится к значению тяги в пустоте, т. е. влияние члена p_нF_a будет пренебрежимо мало.

Полученные ранее зависимости для расчета тяги сопла справедливы при условии независимости параметров течения газа в сопле от давления окружающей среды. Для расчета тяги при наличии скачка уплотнения в сопле необходимо знать местоположение скачка уплотнения и закономерности изменения параметров газового потока за скачком. Однако из-за сложности процесса до настоящего времени нет надежной теоретической методики расчета, поэтому целесообразно проводить расчет на основе полуэмпирических зависимостей, позволяющих определить местоположение скачка уплотнения и параметры газового потока за ним. На течение газа в сопле со скачком уплотнения большое влияние оказывает угол раствора сопла 2 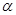. При углах раствора сопла 2 30⁰ давление за скачком уплотнения р ₂ близко к давлению окружающей среды р _н, и восстановление давления за скачком уплотнения р ₂ /р _н близко к единице. При углах 2 < 30⁰ давление за скачком уплотнения резко отличается от давления окружающей среды, и это отличие тем больше, чем больше расчетное значение числа М _а на срезе сопла и глубина проникновения скачка в сопло, т. е. восстановление давления за скачком уплотнения р ₂ / р _н < 1.

На основе экспериментальных исследований конических сопл, проведенных на кафедре "Летательные аппараты", установлено, что давление в точке отрыва зависит от местоположения отрыва, характеризуемого отношением М₁ / М _а, угла раствора сопла 2 и расчетного числа Маха на срезе сопла М _а. Если М₁ / М _а < 0,92, то давление перед скачком р ₁ можно определить по следующей зависимости:

,

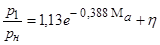где – функция, учитывающая влияние угла раствора сопла на давление в точке отрыва.

Учитывая, что до скачка уплотнения течение можно считать изоэнтропическим, число Маха перед скачком получим из формулы (1.3) для изоэнтропического течения газа:

.

Давление за скачком уплотнения р ₂ и значение числа Маха за скачком можно определить по эмпирическим зависимостям

,

.

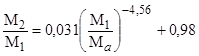По найденным значениям параметров до скачка и после него можно определить тягу сопла. Тягу, снимаемую с внутреннего контура, можно представить как сумму тяг, снимаемых до скачка уплотнения и после него:

,

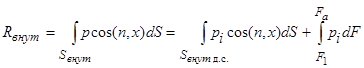где S_{внут. д .с.} – поверхность сопла до скачка уплотнения; F ₁ – площадь сечения сопла в месте расположения скачка.

Интеграл 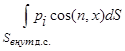определяют по обычным зависимостям, так как до скачка уплотнения происходит безотрывное течение газа в сопле, и тогда

. (2.12)

При p ₂ = p_н . При р ₂ 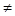р_н определение 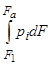осложняется неизвестным характером восстановления давления за скачком уплотнения. Экспериментальные данные показывают, что в этом случае давление на срезе сопла равняется давлению окружающей среды. Поэтому, пренебрегая криволинейным характером изменения, средние давления, действующие на стенки сопла от местоположения скачка уплотнения до среза сопла (на участках lm и mn рис. 15), можно определить как средние арифметические

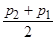и .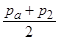

Тогда

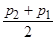= (F ₂ – F ₁) + 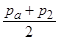(F_a – F ₂), (2.13)

а тяга, полученная с внешнего контура сопла, будет определяться как

R_внеш = p_н F_a. (2.14)

Используя зависимости (2.12)... (2.14), можно получить выражение для расчета тяги сопла с большим углом раствора (2 30⁰), т. е. для p_a = p_н

,

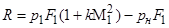а для сопла с малым углом раствора (2 < 30⁰), т. е. для p_a ¹ p_н:

.

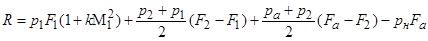назад

Дата добавления: 2014-12-26