Интегрирование уравнений Эйлера

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ ТЕКУЧЕГО ТЕЛА (УРАВНЕНИЯ ЭЙЛЕРА)

Пусть 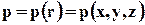- давление в жидкости. Выделим внутри жидкости куб с бесконечно малыми рёбрами dx, dy, dz и рассмотрим его равновесие под действием объёмных и поверхностных сил (рис.2.2).

Приравняем к нулю сумму проекций на ось х всех сил, действующих на куб.

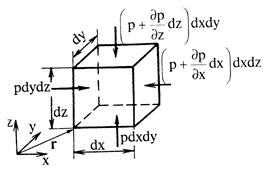Рис. 2.2. К выводу дифференциальных уравнений равновесия текучего тела

Плотность распределения массовой (объёмной) силы обозначим , тогда объёмная сила, действующая на куб, будет иметь проекцию на ось х, равную .

Поверхностные силы на грани, нормальные осям y и z, дают нулевую проекцию на ось х, так как касательные напряжения в условиях гидростатики равны нулю. В пределах куба считаем, что в разложении р(х,у,z) в ряд Тейлора можно принять в расчёт лишь члены, линейно зависящие от приращения координат. Обозначим давление на левую грань куба, перпендикулярную оси х, через р(х,у,z), при этом на правой грани давление будет равно . Если считать эти грани элементарными площадками в отношении давления, то проек­ция на ось х силы давления на левую грань равна р×dy×dz, а на правую равна 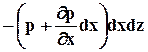. Сумма проекций всех поверхностных сил на ось х при этом окажется равной

.

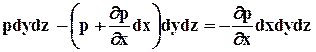Приравняв нулю сумму проекций поверхностных и объемных сил на ось х, имеем:

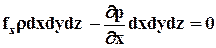. (2.2.1)

Разделив все слагаемые на р×dx×dy×dz, получим первое уравнение рав­новесия. Два других уравнения выведем аналогичным образом, проекти­руя силы на оси у и z. В результате получим систему дифференциальных уравнений равновесия (покоя) текучего тела (уравнений гидростатики Эй­лера):

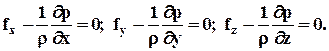(2.2.2)

Введём единичные векторы i, j и k, соответствующие координатным осям х, у и z:

. (2.2.3)

Умножим (2.2.2) на i, j и k, соответственно, и сложим их:

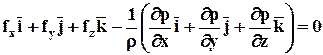
или в векторной форме

. (2.2.4)

Векторное уравнение (2.2.4) равносильно системе трёх уравнений (2.2.3), где вектор grad p определяется через свои проекции на координатные оси в виде

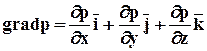(2.2.5)

либо в матричной форме

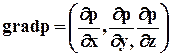. (2.2.6)

Пусть вектор f имеет потенциал, т.е. существует такая функция U(x, у, z), что

или 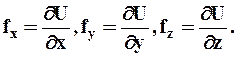(2.3.1)

При этом уравнение (2.2.4) для однородной несжимаемой жидкости (р = const) примет вид

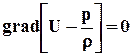. (2.3.2)

Интеграл уравнения (2.3.2) дает равенство

, (2.3.3)

которое представляет собой общую форму интеграла уравнений гидро­статики, когда объемные силы имеют потенциал. Если внешние объем­ные силы не имеют потенциала, то в поле таких сил жидкость не может находиться в состоянии покоя.

Рассмотрим частные случаи объемных сил.

Внешняя объемная сила - сила тяжести. Пусть в декартовой систе­ме координат ось z направлена вверх. Используя (2.3.1), установим, что потенциал силы тяжести:

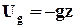, (2.3.4)

где g - ускорение свободного падения, при этом

.

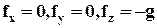Подставим (2.3.4) в (2.3.3):

.

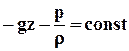Обозначив через g удельный вес (g = rg), получим:

или 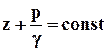. (2.3.5)

Это закон распределения гидростатического давления в поле силы

тяжести. Обозначим через р₀ давление на свободной поверхности, или поверхностное давление, и найдём форму свободной поверхности из условия, что на ней р = р₀ = const. Из (2.3.5) следует, что такая поверхность, координаты которой обозначим через z₀, представляет собой горизонтальную плоскость:

Рис.2.3. Гидростатическое давление в поле силы тяжести

. (2.3.6)

Определённое таким образом давление называется абсолютным давлением и обозначается через р_А. Представим на рис. 2.3 замкнутый сосуд, ча­стично заполненный жидкостью. Давление на сво­бодной поверхности равно р₀. Если h_M – это рас­стояние от свободной поверхности до точки М (заглубление точки), а начало координат распо­ложено на свободной поверхности, так что h_M = -z (рис. 2.3), то в точке М абсолютное давление

, (2.3.7)

где р_в = gh - весовое давление, т.е. давление, обусловленное весом жид­кости.

Обычно в технических приложениях используют не абсолютное дав­ление р_А, а его отклонение от атмосферного давления р_а. Если Р_А > Р_а, то избыточным давлением р_и называется превышение давления в точке над атмосферным:

р_{и =} р_А– р_а. (2. 3.8)

Если на свободную поверхность действует атмосферное давление, то весовое давление в жидкости равно избыточному, и абсолютное давление в любой точке внутри жидкости согласно (2.2.7) можно записать в виде

р_а = Р₀ + Р_в = Р_а + gh = Р_а + Р_и. (2. 3.9)

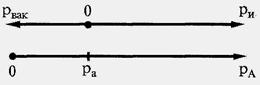  Рис.2.4. Пояснения к определению избыточного и вакуумного давлений

При условии Р_А < р_а недостаток давления в точке до атмосферного называется вакуумом:

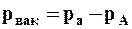. (2.3.10)

Введённые выше определения избыточного давления р_и и давления вакуума р_вак представлены на рис. 2.4 в виде переноса начала отсчёта давления в точку р_а.

Дата добавления: 2014-12-26