Гидромеханическая интерпретация теоремы Остроградского - Гаусса

Зафиксируем неподвижную в пространстве контрольную поверхность А, ограничивающую контрольный объём V. Сквозь эту поверхность протекает жидкость со скоростью 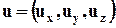. Выделим на ней элементарную площадку dА. Единичный вектор нормали к площадке 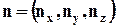. Если воспользоваться ортами i, j, k, то

.

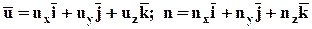Обозначим модуль скорости 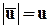; по определению 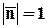. Скалярное произведение двух векторов можно выразить через их проекции:

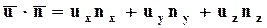, (3.4.1)

а также через модули векторов и угол между ними,

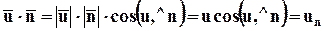(3.4.2)

где u_n - нормальная к поверхности dА составляющая скорости.

Таким образом,

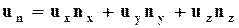. (3.4.3)

Используя (3.4.3), запишем объёмный расход жидкости Q через поверхность dА:

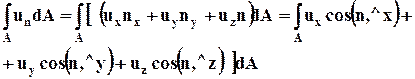. (3.4.4)

Согласно теореме Остроградского - Гаусса имеем

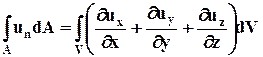. (3.4.5)

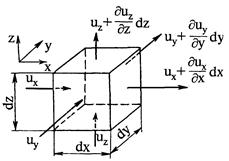Рис. 3.8. Определение расхода жидкости сквозь поверхность элементарного параллелепипеда

Доказательство этой зависимости проведём на основе гидромеханических представлений.

Зафиксируем в пространстве параллелепипед с бесконечно малыми рёбрами dx, dy, dz, поверхностью D_iА и объёмом D_iV = dxdydz.

На каждой грани параллелепипеда значение u_n вследствие её малости постоянно и равно проекции скорости на координатную ось, к которой эта грань нормальна.

Пусть проекции скорости имеют направления, указанные на рисунке. Расход жидкости 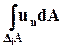, протекающий сквозь поверхность D_iА, определим как разность между объёмом жидкости, вытекающей из параллелепипеда в единицу времени:

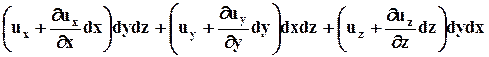
и объём жидкости, втекающей в него за то же самое время:

.

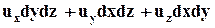В результате имеем

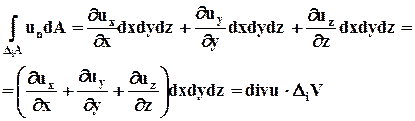
или

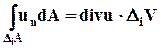, (3.4.6)

где div u - дивергенция вектора скорости, которая определяет собой скалярную величину, определяемую равенством

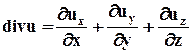. (3.4.7)

Если жидкость несжимаемая, то из закона сохранения массы следует, что объём жидкости, втекающей в элементарный объём D_iV равен объёму жидкости, вытекающей из него, так что

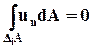. (3.4.8)

Поскольку объём не может быть равным 0, из уравнения (3.4. 6) следует, что в случае несжимаемой жидкости

div u = 0. (3.4.9)

Уравнение (2.4.9) называют уравнением несжимаемости жидкости. Оно справедливо в случае неустановившегося движения жидкости, когда для каждого момента времени и в каждой точке потока.

Чтобы обобщить равенство (3.4.6) для произвольного объёма V, ограниченного произвольной поверхностью А (рис.3.9.) разобьём V на элементарные параллелепипеды. Для каждого из них можно записать равенство (3.4. 6).

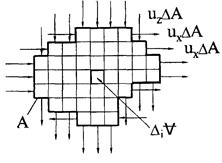Рис.3.9. Определение расхода сквозь произвольную контрольную поверхность

Складывая все эти равенства, можно заметить, что в левой части каждый из интегралов по поверхности D_iА состоит из шести слагаемых по числу граней параллелепипедов. При этом все слагаемые, которые относятся к поверхностям, разделяющим параллелепипеды, взаимно уничтожаются, так как каждая такая поверхность входит в поверхностные интегралы для двух соседних параллелепипедов, и тот объём жидкости, который вытекает из одного параллелепипеда, втекает в другой. Останутся только те части от интегралов 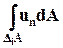, которые относятся к тем граням элементарных параллелепипедов, которые совпадают с контрольной поверхностью А. Следовательно, в левой части сумма интегралов, относящихся ко всем параллелепипедам, будет равна

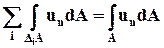. (3.4.10)

В правой части суммы всех уравнений (3.4. 6) по определению интеграла как предела суммы бесконечно малых слагаемых имеем

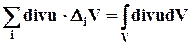(3.4.11)

Таким образом, для объёма V произвольной формы справедливо равенство

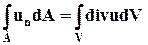(3.4.12)

Представив 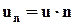, получим

,

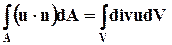что и составляет содержание теоремы Гаусса - Остроградского.

Дата добавления: 2014-12-26