Операции над тензорами

1. Умножение тензора на скаляр есть новый тензор, все компоненты которого умножены на этот скаляр (шаровой тензор):

.

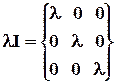2. Сумма тензоров есть новый тензор с компонентами, являющимися суммой одноимённых компонент слагающих тензоров. Так доля Т = Т´ + T´´ должна быть t_ik = t´_ik + t´´_ik. То, что такая сумма есть тензор, следует из линейности формул (4*).

3. Тензор, обладающий свойством t_ik = t_ki, называется симметричным. Если таблицу компонент такого тензора «повернуть» вокруг главной диагонали (то же, что и у определителя), то получится тот же самый тензор.

4. Пусть имеется тензор Т с компонентами t_ik.Составим таблицу с компонентами t_ki (т.е. повёрнутую вокруг главной диагонали). Можно показать, что она также определяет тензор, который называется сопряжённым и обозначается Т*. Очевидно, что (T*)* = T.

5. Тензор, у которого t_ik = - t_ki, называется антисимметричным. Из определения следует, что t_ii = - t_ii, т.е. t_ii = 0 – компоненты главной диагонали равны 0. Антисимметричный тензор всегда можно записать в виде .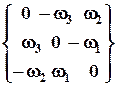

6. Всякий тензор можно разложить на сумму симметричного и антисимметричного тензоров: Т = ½ (Т + Т*) + ½ (Т - Т*). Легко проверить, что в первой скобке стоит симметричный, а во второй – антисимметричный тензор.

7. Пусть дан тензор Т и вектор 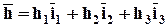.Скалярное произведение тензора Т на вектор 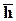справа есть новый вектор 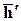, обозначаемый (Т, 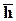), компоненты которого равны

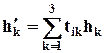(i = 1,2,3).

8. Скалярное произведение тензора Т на вектор 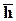слева есть вектор 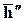, обозначаемый (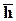,Т), компоненты которого равны

.

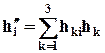9. Из приведённых определений операций ясно, что они должны обладать ассоциативностью и дистрибутивностью, т.е., например,

(Т₁ + Т₂ 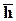) = (Т₁, 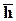) + (Т₂, );

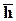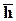( ₁ + 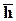₂, Т) = ( 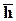₁, Т) + ( 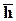₂, Т);

(l 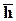, Т) = (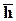, lТ) = l (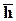, Т).

Но коммутативностью эти операции не обладают, т.е. в общем случае (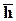, Т) ¹ (Т, 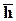). Если Т – симметричный тензор, то равенство выполняется.

10. Пусть даны тензоры А, В с компонентами a_ik и b_ik. Скалярное произведение тензора А на тензор В (А, В)есть новый тензор Т, компоненты которого вычисляются по формулам:

.

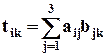Это определение совпадает с определением матричного умножения. Компонент t_ik получается умножением строки с номером i тензора А на столбец с номером j тензора В. Например, t₂₃ = а₂₁b₁₃ + а₂₂ b₂₃ + а₂₃ b₃₃.

11. Скалярное произведение тензоров не обладает свойством коммутативности, т.е. вообще говоря, (А,В) ¹ (В,А).

Перечислим некоторые свойства, которыми оно обладает:

(lА,В) = (А,lВ) = l (А,В); (l - скаляр);

(А₁ + А₂, В) = (А₁,В)+ (А₂,В);

(А,В₁ + В₂) = (А,В₁) + (А,В₂);

[(А,В), С) = (А,(В,С)].

4. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ТВЁРДЫХ СРЕДАХ

Дата добавления: 2014-12-26