Поток гидромеханической характеристики через поверхность

Законы механики формулируются для выделенных механических систем, или совокупностей физических тел. Для сплошной среды это жидкий объём, т.е. выделенный движущийся объём жидкости (текучего тела), сохраняющий при своём движении все составляющие его части (жидкие частицы). Это понятие соответствует лагранжеву методу описания движения текучих тел.

Эйлеров метод позволяет использовать для решения задач гидромеханики выделенную часть пространства, обычно неподвижную (не связанную с движением среды), которую называют контрольным объёмом. Контрольный объём ограничивается контрольной же поверхностью, сквозь которую течёт сплошная среда. Использование контрольной поверхности и контрольного объёма приводит к использованию понятия потока гидромеханической характеристики (массы, кинетической энергии), т.е. количества этой характеристики, проносимой жидкостью в единицу времени сквозь фиксированную поверхность.

Рис.3.7. Поток скорости сквозь контрольную поверхность

Зафиксируем в пространстве, занятом движущейся жидкостью, поверхность А и выделим на этой поверхности около точки с координатами элементарную площадку dA(рис.3.7). Скорость жидкости в этой точке равна n - единичный вектор нормали к поверхности в этой же точке. Нормальная к поверхности составляющая скорости будет при этом равной . Объём жидкости, протекающей в единицу времени через площадку dA, равен .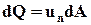

В элементарном объёме dQ содержится dQ_B гидромеханической характеристики В, которая проносится жидкостью за единицу времени через площадку dA:

(3.3.1)

Поток Q_B гидромеханической характеристики В через контрольную поверхность Ф (количество характеристики, проносимое жидкостью за единицу времени через поверхность А) составляет

(3.3.2)

Поток гидромеханической характеристики В через контрольную поверхность единичной площади (подынтегральное выражение b называется плотностью потока гидромеханической характеристики.

Если принять 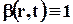, то из (3.3.1) следует, что при этом гидромеханической характеристикой является объём жидкости. Объём жидкости, протекающий через контрольную поверхность за единицу времени, или поток объёма жидкости называется расходом (объёмным расходом) Q:

. (3.3.3)

Если принять , то гидромеханической характеристикой в этом случае будет сама масса жидкости. Поток массы жидкости (масса жидкости, протекающая за единицу времени) через контрольную поверхность А называется массовым расходом Q_м:

. (3.3.4)

Если положить , то получим поток Q_k кинетической энергии через контрольную поверхность:

. (3.3.5)

Положив 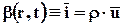, получим поток количества движения Q_I:

. (3.3.6)

В интегралах (3.3.3.)-(3.3.6) выражения 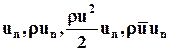представляют собой плотности потоков объёма, массы, кинетической энергии, количества движения, соответственно. Если в поле скорости u (или любой другой векторной величины) мысленно провести некоторую поверхность S и в каждой точке её задать нормаль , то для определения объёма жидкости, протекающей за единицу времени сквозь поверхность S, необходимо вычислить интеграл:

.

Поток скорости сквозь замкнутую поверхность S, отнесённый к единице объёма V, заключённого внутри S, называется расхождением или дивергенцией скорости, т.е.

.

В декартовой системе координат дивергенция скорости вычисляется по формуле:

.

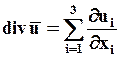Отсюда видно, что дивергенция скорости определяет скорость объёмного расширения жидкости в бесконечно малой окрестности данной точки. Поэтому поток скорости через замкнутую поверхность s должен быть равен расширению всего объёмаvжидкости внутри s, то есть

(3.3.7)

Это равенство называется формулой Гаусса.

Дата добавления: 2014-12-26