Поля в гидродинамике

При изучении движения жидкости рассматривают её как сплошную среду. Таким образом, рассматривают не движение конечного числа отдельных частиц, а поля различных физических величин: скорости, плотности, давления и т.д. Такие поля можно назвать материальными полями. Математически эти поля описывают системой функций от координат и времени. Такой подход типичен не только для механики сплошных сред, но и для ряда других областей физики.

В общем случае поле является пространственным (трёхмерным), иногда задачу упрощают, и рассматривают двумерные (плоские) или одномерные поля. В этом случае полагают, что физические величины зависят от одной или двух пространственных координат.

Если физические величины не зависят от времени, то поле называют стационарным, в противном случае - нестационарным.

При математическом описании полей предполагают, что существуют пределы значений физических величин в точке. Такой подход упрощает физическую реальность, так как не учитывает дискретность строения материи, но такая абстракция оправдана, нужно только разумно ограничивать область полученных результатов.

Так как в практических задачах размеры обтекаемых тел намного порядков больше молекулярных размеров, то в этих задачах жидкость можно рассматривать как сплошную среду.

Скалярным называют поле, которое в каждой точке пространства характеризуют одним числом. Скалярное поле описывают одной функцией, зависящей от трёх координат. (Например, поле плотности или температуры).

Основное свойство скалярной функции а(х₁,х₂,х₃) состоит в том, что её численное значение не меняется при преобразовании координат.

Если перейти от старой х₁,х₂,х₃ к новой х^¢₁,х^¢₂,х^¢₃ системе координат, то значения плотности или температуры в фиксированной точке пространства, естественно, не изменяются:

а (х^¢₁,х^¢₂,х^¢₃) = а (х₁,х₂,х₃).

Векторным называют поле, которое в каждой точке пространства характеризуется величиной и направлением.

Например, поле скоростей жидкости. Вектор 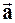в пространстве трёх измерений может быть задан тремя компонентами:

а₁(х₁,х₂,х₃), а₂(х₁,х₂,х₃), а₃(х₁,х₂,х₃),

то есть, тремя функциями от трёх переменных. Это можно записать в виде матрицы-столбца:

а ÜÞ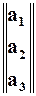

Введём новую декартову систему координат с тем же началом, но с другим направлением осей.

Пусть l _ij - направляющий косинус оси x^¢_j относительно оси x_i (i = 1,2,3; j = 1,2,3). Вычислим проекции того же вектора на новые оси координат:

a^¢₁ = l ₁₁ a₁ + l ₂₁ a₂ + l_{3 1} a₃;

a^¢₂ = l ₂₁ a₁ + l ₂₂ a₂ + l₂₃ a₃;

a^¢₃ = l ₃₁ a₁ + l ₃₂ a₂ + l₃₃ a₃.

Следовательно, вектор подчиняется определённому закону преобразования его компоненти отличается от скалярной величины, численное значение которой не меняется при преобразовании координат.

То есть,сам вектор не меняется в новых координатах, а меняются его компоненты.

Это выражение можно представить в индексной форме записи как сумму:

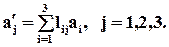
Или ещё более короткой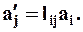

При такой записи пользуются двумя правилами:

1. Соглашение о суммировании. По индексу, встречающемуся дважды (немой индекс), производят суммирование от 1 до 3.

2. Соглашение о ранге. Индекс, встречающийся один раз (свободный индекс), пробегает значения от 1 до 3.

Таким образом, уравнение с одним свободным индексом означает запись трёх уравнений.

Помимо скалярных и векторных полей в механике сплошной среды рассматриваются ещё и тензорные поля.

Многие задачи физики и механики сплошной среды приводят к понятию тензора. Тензор, хотя и является обобщением понятия вектора, имеет гораздо более сложный характер. Разница заключается в том, что вектор просто интерпретируется геометрически, у тензора такого наглядного представления не существует.

Описание происходит в прямолинейных (декартовых) системах координат. Координаты обозначаем х₁, х₂, х₃, единичные векторы по осям - i₁,i₂, i₃.

Предположим, что в результате вращения осей координат как единого целого вокруг начала координат, мы перешли к новой системе координат Ox₁´x₂´x₃´. Обозначим косинус угла между осями x_i и x´_k старой и новой системы a_ik = cos (x´_i^x_k). Для удобства пользования дальнейшими формулами приводим таблицу.

Таблица 3.1

	х1	х2	х3
х´1	a11	a12	a13
х´2	a21	a22	a23
х´3	a31	a32	a33

Теперь перейдём к определению тензора. Пусть каждому направлению 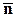соответствует вектор 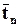(не обязательно коллинеарный n).

Направлениям осей соответствуют векторы 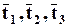, разложение которых опишем подробно:

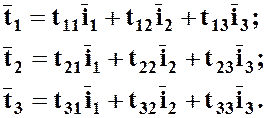(3.6.1)

Если векторы 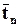для любого направления 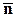выражаются лишь через 3 вектора 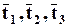согласно формуле

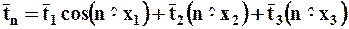, (3.6.2)

то множество векторов 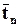образует тензор Т.

Обозначим векторы, определяемые тензором для направлений новых осей 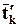. Подставляя в предыдущее выражение (2.6.2) вместо 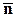направления новых осей (по очереди), получим:

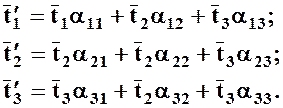(3.6.3)

Эти условия равносильны (2.6.2) и их можно взять за новое определение тензора, если для каждой системы координат имеется тройка векторов 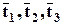, преобразующаяся по формулам (2.6.3) в тройку 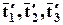, отвечающую другой системе координат, то этим определяется тензор.

Аналогичное определение можно дать и для вектора, если в уравнении (2.6.3) заменить векторы на проекции вектора. Поэтому тензор является обобщением вектора. Формулы (2.6.3) можно записать в сокращённом виде

.

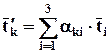Тензор определяется векторами 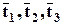, которые в свою очередь определяются своими компонентами (3.6.1). Поэтому тензор вполне задаётся 9 числами, которые называются компонентами тензора, и обычно записываются в виде

.

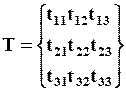Из (2.6.1) и (2.6.3) можно получить формулы преобразования компонент тензора при переходе к новой системе координат:

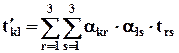, (3.6.4)

где t´_kl – компоненты в новой системе.

Эти формулы можно также взять за определение тензора.

Простейшими примерами являются нулевой и единичный тензоры.

Согласно (2.6.4) у нулевого тензора в любой системе координат компоненты равны 0.

.

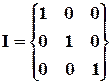Для того, чтобы в дальнейшем не испытывать трудностей при использовании тензоров, запишем некоторые математические правила.

Дата добавления: 2014-12-26