Метод последовательного дифференцирования

Аналитические методы

Рассмотрим уравнение

(9.1)

с начальными условиями 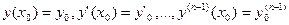. Предположим, что искомое частное решение 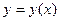может быть разложено в ряд Тейлора по степеням разности :

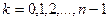Начальные условия непосредственно дают нам значения при . Значение найдем из уравнения (9.1), подставляя и используя начальные условия:

.

Значения последовательно определяются дифференцированием уравнения (9.1) и подстановко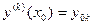й , при .

Доказано, что если правая часть уравнения (9.1) в окрестности точки 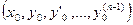есть аналитическая функция своих аргументов, то при значениях x, достаточно близких к 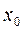, существует единственное решение задачи Коши, которое разлагается в ряд Тейлора. Тогда частичная сумма этого ряда будет приближенным решением поставленной задачи.

Аналогично применяется метод последовательного дифференцирования и для решения систем дифференциальных уравнений.

Пример 9.1 Найти первые семь членов разложения в степенной ряд решения уравнения y^'' +0.1(y')²+(1+0.1 x) y = 0 с начальными условиями y (0)=1, y ^'(0)=2

Решение уравнения ищем в виде ряда

Непосредственно из начальных условий имеем y (0)=1, y ^'(0)=2

Разрешим уравнение относительно y^'';

y^{' '}=-0.1(y^')²-(1+0.1 x)

используя начальные условия, получим

y^'' (0)=-0.1·4-1·1=-1.4

Дифференцируем по x обе части уравнения последовательно получим:

y^''' =0.2 y^' · y^'' -0.1(xy^' + y)- y^' y^{'' '}(0)=-1.54

y ⁽⁴⁾=-0.2(y^' y^''' +(y^'')²)-0.1(xy^{' '}+2 y^')- y^'' y ⁽⁴⁾(0)=1.224

y ⁽⁵⁾= -0.2(y^' · y ⁽⁴⁾+3 y^'' y^''') -0.1(xy^''' +3 y^'')- y^''' y ⁽⁵⁾(0)=0.1768

y ⁽⁶⁾(0)= -0.2(y^' · y ⁽⁵⁾+4 y^'' y ⁽⁴⁾+3(y^''')²)-0.1(x y ⁽⁴⁾+4 y^''')- y ⁽⁴⁾ y ⁽⁶⁾(0) =-0.7308

Искомое решение приближенно запишется в виде:

y (x)≈1+2 x -0.7 x ²-0.2567 x ³+0.051 x ⁴+0.00147 x ⁵-0.00101 x ⁶

Пример 9.2. Найти первые четыре члена разложения в степенной ряд решения y = y (x) z = z(x) системы с начальными условиями y (0)=1 z (0)=0

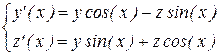
Функции y (x) и z (x) ищем в виде степенных рядов

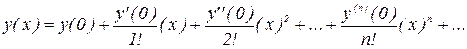
при х =0 из уравнений системы следует, что y (0)'=1, z (0)'=0

Дифференцируем по х уравнения системы.

Находим y ''(0)=1, z ''(0)=1

Продифференцируем по х уравнения системы еще раз.

y ''' (0)=0, z''' (0)=3

Подставляя найденные значения производных в ряды, получим:

y (x)≈1+ x -0.5 x ², z (x)≈ 0.5 x ²-0.5 x ³

Дата добавления: 2014-12-26