Третий улучшенный метод Эйлера

Второй улучшенный метод Эйлера

Первый улучшенный метод Эйлера

Модифицированные методы Эйлера

Первый улучшенный метод состоит в том, что сначала вычисляют промежуточные значения.

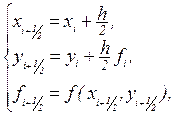
а затем полагают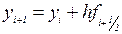

По второму улучшенному методу – методу Эйлера-Коши – сначала определяют «грубое приближение» 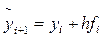, затем вычисляют значение функции 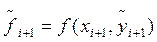и приближенно полагают 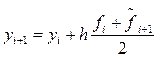. Остаточные члены первого и второго улучшенных методов Эйлера на каждом шаге имеют порядок .

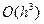Метод Эйлера-Коши можно еще более уточнить, применяя итерационную обработку каждого значения 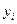. А именно, исходя из грубого приближения 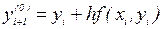, построим итерационный процесс 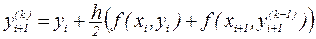. Итерации продолжаем до тех пор, пока в двух последовательных приближений 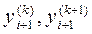не совпадут соответствующие десятичные знаки. После этого полагаем .

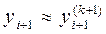Как правило, при достаточно малом h, итерации быстро сходятся. Если после трех-четырех итераций не произошло совпадения нужного числа десятичных знаков, то следует уменьшить шаг расчета h.

Оценка погрешности в точке 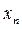может быть получена с помощью двойного пересчета: расчет повторяют с шагом 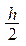, и погрешность более точного значения 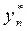оценивают приближенно так

,

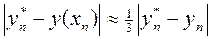где 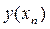- значение точного решения дифференциального уравнения.

Дата добавления: 2014-12-26