Кинематический и структурный анализ плоских стержневых систем

Классификация конструкций и их расчетных схем

Конструкции и их расчетные схемы классифицируют по различным признакам: геометрическим, кинематическим, по особенностям работ и т.п.

По геометрическим признакам конструкции подразделяются на плоские и пространственные. В плоской стержневой конструкции осевые линии всех стержней расположены в одной плоскости.

По кинематическим признакам различают системы: геометрически неизменяемые неподвижные без избыточного числа внешних и внутренних связей и с избыточным числом связей; геометрически изменяемые, например, гибкие нити.

По особенностям работы опор различают распорные и безраспорные системы. Для распорных систем характерно наличие горизонтальных составляющих опорных реакций при вертикальной нагрузке.

По особенностям работы стержней конструкции различают следующие типы конструкций: балки, рамы, арки, фермы, комбинированные и висячие системы (рис.1.6).

Балочные конструкции относятся к безраспорным. Элементы балочной конструкции работают в основном на изгиб (рис.1.6.а).

Рамные системы (рис.1.6.б) могут быть безраспорными (1,2) и распорными (3). Рама – это стержневая система из стоек (вертикальные элементы) и ригелей (горизонтальные элементы), соединенных жесткими и шарнирными узлами. Стержни рамы работают на изгиб и на растяжение – сжатие.

Арка (рис.1.6.в) – это распорная система, состоящая из одного или двух (соединенных шарниром) криволинейных элементов. Арки бывают трехшарнирные (1), двухшарнирные (2) и бесшарнирные (3). Элементы арки работают в основном на сжатие.

Ферма – стержневая система, изображаемая на расчетной схеме с шарнирными узлами (рис.1.6.г). Стержни фермы работают на осевое растяжение – сжатие.

Комбинированная система (рис.1.6.д) – это система, состоящая из балки и стержней, работающих на осевое растяжение – сжатие.

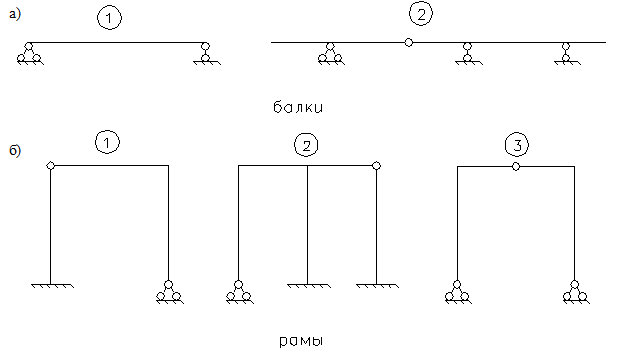
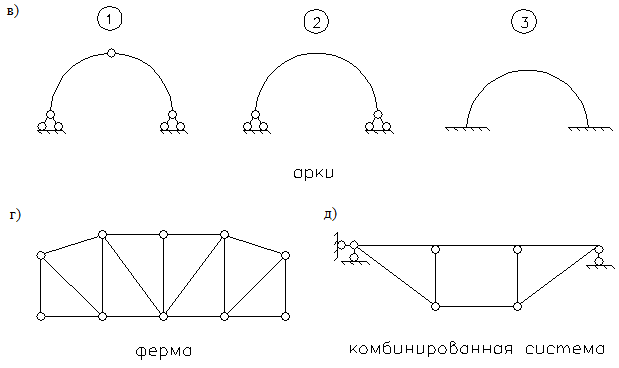
Рис.1.6. Виды расчетных схем

Основным элементов висячей системы является гибкая нить, работающая только на растяжение. Кроме гибкой нити висячая система содержит другие элементы, работающие на изгиб (рис.1.7).

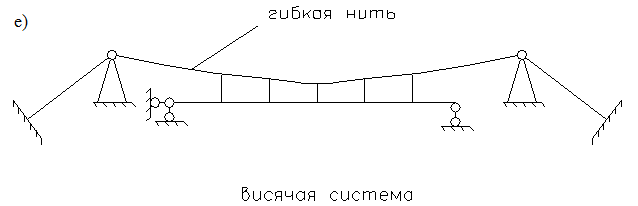
Рис 1.7. Пример висячей системы

Реальные строительные конструкции и сооружения не должны изменять свою форму и размеры под действием нагрузки без деформации элементов их образующих. Такие конструкции и сооружения называются геометрически неизменяемыми. Очевидно, что и расчётные схемы (системы) таких конструкций должны быть геометрически неизменяемыми.

1.4.1. Кинематический анализ стержневых систем

Для того чтобы установить неизменяемость системы, необходимо проводить её кинематический анализ. При кинематическом анализе плоской стержневой системы определяется число степеней свободы системы по формуле

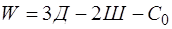(1)

где Д - число дисков, образующих систему;

Ш - число простых шарниров, соединяющих диски;

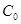- число опорных связей.

Число степеней свободы системы W равно числу независимых геометрических параметров, определяющих положение всех точек системы при возможном перемещении её элементов.

Определённое по формуле (1) число степеней свободы системы называется степенью изменяемости системы.

Дисками при кинематическом анализе системы называются геометрически неизменяемые части системы. Например, дисками являются (рис. 1.8):

· отдельные стержни, образующие систему;

· несколько стержней, соединенных жесткими узлами (ломаные стержни);

· три стержня, соединённых шарнирами и образующие треугольник.

а) б) в)

Рис. 1.8. Примеры дисков

Диск на плоскости имеет три степени свободы, его положение при перемещении можно описать тремя геометрическими параметрами:

линейными перемещениями u и v;

углом поворота .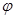

Поэтому система из Д свободных дисков имеет 3 Д степеней свободы.

Простым шарниром называется шарнир, соединяющий на расчётной схеме два стержня (рис. 1.9). Если шарниром на расчётной схеме соединяется С стержней, то в этом случае число простых шарниров определяется по формуле

Ш=С – 1. (2)

Ш=1 Ш=2

Простой шарнир Сложный шарнир

Рис. 1.9. Простой и сложный шарниры.

Каждый простой шарнир отнимает у системы две степени свободы.

Число опорных связей 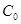определяется типом опор на расчётной схеме. На рис. 1.10 приведены типы опор и соответствующее им число опорных связей С_{0 .}

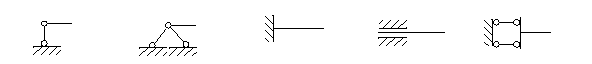
C₀=1 C₀=2 C₀=3 C₀=2 C₀=2

Рис. 1.10. Типы опор и соответствующее им число связей

Каждая опорная связь отнимает у системы одну степень свободы.

Полученное по формуле (1) значение W позволяет делать следующие выводы:

· Если W>0, то система является геометрически изменяемой и по определению не может служить в качестве расчётной схемой сооружения.

· Если W<0, то это условие необходимое, но недостаточное для того, чтобы система была геометрически неизменяемой. В этом случае требуется проводить дополнительно структурный анализ системы.

1.4.2. Структурный анализ стержневой системы.

Структурный анализ системы заключается в геометрическом анализе её структуры с целью доказательства геометрической неизменяемости исследуемой системы.

Для анализа неизменяемости системы необходимо:

· выделить неизменяемые части системы - диски;

· провести анализ вида и структуры связей, соединяющих диски между собой.

В плоских стержневых системах связями являются:

· Стержни, присоединённые к дискам шарнирами. Такая связь уменьшает число степеней свободы системы на единицу.

· Простые шарниры, эквивалентные двум стержневым связям.

При структурном анализе за неизменяемую часть системы - диск можно принимать:

· стержень;

· несколько стержней, соединенных жестким узлом;

· часть системы, состоящую из дисков связанных между собой определённым образом.

В последнем случае нужно руководствоваться следующими правилами образования неизменяемых систем из двух и трёх дисков.

Два диска образуют геометрически неизменяемую систему- диск:

· если они связаны между собой с помощью трёх стержней, осевые линии которых не параллельны и не пересекаются в одной точке (рис. 1.11.а);

· или если они связаны шарниром и стержнем, осевая линия которого не проходит через шарнир (рис. 1.11.г).

а) б) в) г)

диск диск

диск диск

неизменяемая изменяемая мгновенно изменяемая диск

Рис. 1.11. Системы из двух дисков

Система из двух дисков, соединённых тремя параллельными стержнями является геометрически изменяемой. Если осевые линии трёх стержней, соединяющих два диска, пересекаются в одной точке, то такая система называется мгновенно изменяемой (рис. 1.11.в).

Три диска образуют геометрически неизменяемую систему:

· если каждая пара дисков соединяется двумя стержнями, точки пересечения осевых линий которых не лежат на одной прямой (рис.112.а);

· если два диска соединены между собой шарниром, а с третьим диском двумя стержнями, точка пересечения осевых линий которых не лежат на одной прямой с шарниром (рис. 1.12.б)

· если три диска соединены двумя шарнирами и двумя стержнями, так как показано на рис. 1.12.в, причём точка пересечения осевых линий стержней и два шарнира не лежат на одной прямой;

· если три диска соединены тремя шарнирами, которые не расположены на одной прямой (рис. 1.12.г)

Все указанные способы соединения трёх дисков в геометрически неизменяемую систему можно свести к последнему случаю, если точку пересечения осевых линий двух стержней - связей между двумя дисками, принять за фиктивный шарнир.

а) б) в) г)

Рис. 1.12. Геометрически неизменяемые системы из трёх дисков.

При структурном анализе стержневой системы следует различать два вида связей между дисками - внутренние и внешние. Внутренние связи соединяют диски системы между собой. Внешние связи соединяют диски системы с опорным диском и обеспечивают геометрическую неизменяемость и неподвижность стержневой системы относительно опорного диска. Опорными дисками являются, например, фундамент или другая часть сооружения, которая является внешней по отношению к исследуемой системе. Опорные диски являются неподвижными, их часто называют “землёй”.

Если система дисков, включающая диски стержневой системы и опорный диск, является жёстким единым диском, что такая система является неизменяемой и неподвижной.

Более подробно вопросы кинематического и структурного анализа изложены в учебниках по строительной механике.

1.5. Статически определимые и статически неопределимые стержневые
системы.

Статически определимыми стержневыми системами являются геометрически неизменяемые системы, для которых число степеней свободы, определяемое по формуле (1), равно нулю, то есть. W=0. Реакции опор и внутренние усилия в таких системах могут быть определены только с помощью уравнений равновесия, что значительно упрощает их расчёт.

Статически неопределимыми стержневыми системами являются геометрически неизменяемые стержневые системы, для которых число степеней свободы, определяемое по формуле (1), меньше нуля, то есть W<0. Такие системы имеют избыточное число связей по сравнению с минимально необходимым числом связей для образования геометрически неизменяемой системы. Реакции опор и внутренние усилия в таких системах не могут быть определены только с помощью уравнений равновесия.

Таким образом, с помощью формулы (1) определяется статическая определяемость или неопределяемость стержневой плоской системы.

1.6. Виды нагрузок и их расчётные схемы.

Строительные конструкции предназначены для восприятия внешних нагрузок и воздействий.

Нагрузками являются активные внешние силы. К воздействиям относят изменение температуры, осадку опор

Нагрузки можно разделить:

· по способу их приложения - на распределённые и сосредоточенные,

· по характеру воздействия во времени - на статические и динамические,

· по длительности действия на сооружение - на постоянные и временные.

Реальная нагрузка распределена или по объёму элемента сооружения (сила тяжести, силы инерции) или по поверхности. Но если длина (площадь или объём), на которой действует нагрузка, мала по сравнению с длиной (площадью или объемом) элемента, то нагрузку, действующую по линии (объёму, площади), можно заменить её равнодействующей, то есть сосредоточенной силой, приложенной в точке. На расчётных схемах плоских стержневых систем реальные объёмные и поверхностные нагрузки заменяются нагрузками, распределёнными вдоль линии (линейными нагрузками), сосредоточенными силами и моментами (рис. 1.13).

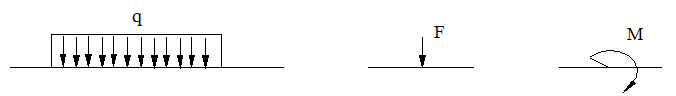(кН/м) (кН) (кНм)

Распределённая нагрузка Сосредоточенная сила Сосредоточенный момент

Рис. 1.13. Схемы нагрузок.

Статические нагрузки - это нагрузки постоянные по направлению и положению, величина которых либо не изменяется, либо изменяется медленно, плавно, без скачков. При статической нагрузке не возникают ускорения масс сооружения или конструкций, либо возникают такие незначительные по величине ускорения, что вызванными ими силами инерции можно пренебречь.

Динамические нагрузки - это нагрузки, которые изменяют либо место приложения, либо направление, величину, либо все эти параметры одновременно или в сочетании. Динамические нагрузки вызывают значительные силы инерции, которыми при расчете нельзя пренебречь.

Постоянные нагрузки действуют на сооружение постоянно. Это собственный вес конструкции, её несущих и ограждающих элементов, вес и давление грунтов и др.

Временные нагрузки - это нагрузки, которые в отдельные периоды работы сооружения могут отсутствовать. Они подразделяются на длительные, кратковременные и особые.

К длительным нагрузкам относят, например, вес временных ограждающих конструкций, вес оборудования. К кратковременным нагрузкам относят, например, снеговую и ветровую нагрузку, вес людей, ремонтных материалов.

К особым нагрузкам относят сейсмические и взрывные нагрузки, воздействия от неравномерной осадки основания.

Основными характеристиками нагрузок являются их нормативные величины, приведённые в СНиП “Нагрузки и воздействия”. Расчёт сооружения производят на так называемые расчётные нагрузки, получаемые из нормативных нагрузок умножением их на различные коэффициенты, приведённые в СниП. Так как временные нагрузки в некоторые периоды эксплуатации сооружения могут отсутствовать, то расчёт сооружения производят на неблагоприятные сочетания постоянных и временных нагрузок с целью определения всех возможных при эксплуатации сооружения напряжённо-деформационных состояний.

Определение нагрузок, действующих на сооружение и его элементы - важнейший этап создания расчётной схемы сооружения. Этот вопрос подробно обсуждается в курсах по проектированию сооружений.

1.7. Примеры расчётных схем и их кинематического анализа.

Дата добавления: 2014-12-26