Методи лінійного програмування

Дані для обчислення

Таблична форма обчислення

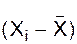
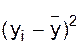
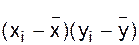
		1,3	1,69	1,3
-4		-4,3	18,49	17,2
		2,8	7,84	8,4
-2		-1,8	3,24	3,6
-3		-3

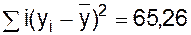
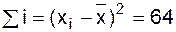
Близькість зв'язку між показниками запуску та випуску вимірю­ється коефіцієнтом кореляції, що обчислюється за формулою

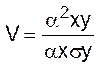. (1.30)

Підставляючи відповідні значення, одержимо:

;

;

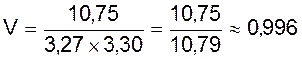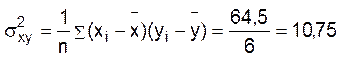Вводячи формулу зв'язку лінійної підстановки (у = a₀ + а_i х), визначимо залеж­ність випуску промислових виробів від їхнього за­пуску. Для цього добирається система нормальних рівнянь:

.

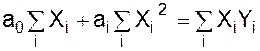Величини Sx₂² і Sx_iy_i представлені в наступній табл. 1.8.

Таблиця 1.8

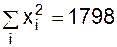
309,6	459,8	150,8	374,0	211,5	180,6

Значення а₀ визначаємо за першим рівнянням:

Підставляючи знайдене вираження а₀ у друге рівняння, знахо­ди­мо значення а_i:

102 (15,9 – 17 а₁) + 1798а₁ = 1686,3

1621,8 – 1734 а₁ + 1798а₁ = 1686,3

64а₁ = 1686,3: 1321,8

64а₁ = 64,5

а₁ = 1,01

а₀ = 15,9 – 17 ´ 1,01

а₀ = 15,9 – 17,17

а₀ = - 1,27

Отже, рівняння регресії в остаточному варіанті має такий ви­гляд:

У = -1,27 +1,01 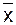(1.31)

Перевірка: 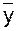= -1,27 +1,01 ´ 17 = -1,27 + 17,17 = 15,9

Методи лінійного програмування застосовуються для розв'язан­ня багатьох екстремальних задач, з якими досить часто приходиться мати справу в економіці. Рішення таких задач зводиться до зна­ход­ження край­ніх значень (максимуму і мінімуму) деяких функцій змінних величин.

Лінійне програмування засноване на рішенні системи лінійних рівнянь (з перетворенням у рівняння і нерівності), коли залежність між досліджуваними явищами суворо функціональна. Для нього характер­ні математичне вираження змінних величин, певний порядок, послі­довність розрахунків (алгоритм), логічний аналіз. Застосовувати його можна тільки в тих випадках, коли досліджувані змінні величини і фак­тори мають математичну визначеність і кількісну обмеженість, коли в результаті відомої послідовності розрахунків відбувається взаємоза­мінність факторів, коли логіка в розрахунках, математична логіка спо­лу­чаються з логічно обґрунтованим розумінням сутності досліджува­ного явища.

За допомогою цього методу в промисловому виробництві, на­при­клад, обчислюється оптимальна загальна продуктивність машин, агре­гатів, поточних ліній (при заданому асортименті продукції й інших за­даних величинах), розв'язується задача раціонального роз­крою мате­ріалів (з оптимальним виходом заготівель). У сільському господарстві він використовується для визначення мінімальної вар­тості кормових раціонів при заданій кількості кормів (за видами і живильними речо­винами, що містяться в них). Задача про суміші може знайти засто­сування й у ливарному виробництві (склад мета­лургійної шихти). Цим же методом вирішується транспортна задача, задача раціонального прикріплення підприємств-споживачів до під­приємств-виробників.

Усі економічні задачі, що розв'язуються з застосуванням ліній­но­го програмування, відрізняються альтернативністю рішень і певними обмежуючими умовами. Вирішити таку задачу – значить вибрати з усіх можливих (альтернативних) варіантів кращий, оптимальний. Важли­вість і цінність використання в економіці методу лінійного програмування по­лягають у тому, що оптимальний варіант вибирається з дуже великої кількості альтернативних варіантів. За допомогою інших способів вирі­шувати такі задачі практично неможливо.

Як приклад розглянемо рішення задачі раціональності викори­стан­ня часу роботи виробничого устаткування.

Відповідно до оперативного плану ділянка шліфування за пер­ший тиждень грудня випустила 500 кілець для підшипників типу А, 300 кілець для підшипників типу Б і 450 кілець для підшипників типу В. Усі кільця шліфувалися на двох взаємозамінних верстатах різної продуктив­но­сті. Машинний час кожного верстата складає 5 000 хв. Трудомісткість операцій (у хвилинах на одне кільце) при виготовленні різних кілець характеризується наступними даними (табл. 1.9).

Таблиця 1.9

Дата добавления: 2014-12-26