Розрахунок повної кількості приходів робітників у комору

Кількість при­ходів в оди­­ницю часу (за 15 хв.)	Кількість приходів, що спо­стеріга­ється, %	Частота приходів, що спо­стеріга­ється, %	Повна кількість приходів робітни­ків (гр.1´гр.2)	Кількість приходів в оди­ни­цю часу (за 15 хв.)	Кількість приходів, що спо­стеріга­ється, %	Частота приходів, що спо­стеріга­ється, %	Повна кількість приходів робітників (гр.1 ´ гр.2)
						7,67
						6,67
		0,33
						5,33
		1,67				4,33
		2,67				3,67
		3,33				3,33
						2,67
		4,33				1,67
		5,33
						0,33
		6,67				0,33
		6,33				99,99
		8,33

Частота приходу двох робітників при 300 спостереженнях дорівнює 0,33 ´ ((1/300) ´ 100)), трьох – 1 ´((3/300 ´ 100))

Для визначення середньої кількості приходів в одиницю часу (l) обчислюється повна кількість приходів (N) як сума добутків кількості приходів (кількості робітників, що прийшли в комору) на кількість приходів, що спостерігається.

Таким чином, середня кількість вимог на обслуговування, тобто середня кількість приходів в одиницю часу (l), складе

(1.35)

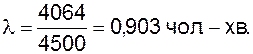
Щоб визначити розподіл імовірностей для тривалості обслуго­ву­вання при припущенні, що закон розподілу експонентний, обчислимо середню тривалість одного обслуговування (Т_обсл) (вона дорівнює 1,6 хв.):

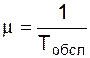(1.36)

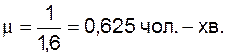
Після цього можна встановити інтенсивність обслуговування (µ).

У випадку, коли l < m, збільшення черги не виникає, тому що задоволення вимог відбувається не раніше їхнього надходження. У нашому прикладі l > m, (0,903 > 0,625) в коморі утвориться черга.

Точно визначити величину черги як випадкову не можна. Можна обчислити ймовірність того, що в момент часу (t) черга буде характе­ризуватися числом вимог Р_n (t):

(1.37)

де Р_n (t) – імовірність відсутності черги.

У тих випадках, коли s ³ 1, імовірність відсутності черги (s₀) зви­чайно береться з графіків (у нашому прикладі s = 1,445).

Для побудови таких графіків скористаємося таблицею значень Р₀ для різних значень s і n (n – кількість комірників в інструментальній коморі).

За даними табл. 1.11, у нашому випадку розглядається много­ліній­на система, коли n ³ 1 (кількість комірників перевищує одиницю).

Таблиця 1.11

Значення Р₀

							…
	0,333	0,363	0,367	0,367	0,367	0,367	0,368
		0,111	0,130	0,134	0,135	0,135	0,135
			0,037	0,046	0,049	0,049	0,050
				0,013	0,016	0,017	0,018

Визначимо середній час чекання (Tс), що складається з серед­нього часу очікування обслуговування в черзі (Точ) і середнього часу обслуговування (Тобсл):

Тс = Точ + Тобсл. (1.38)

У тому випадку, коли в системі працює n комірників, середній час чекання в черзі визначиться за формулою:

при n = 2:

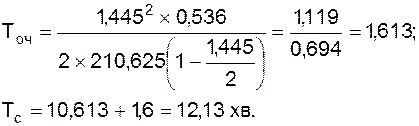
при n = 3:

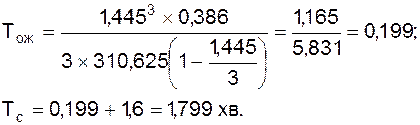
при n = 4:

Припустимо, що у робітника витрати від простоїв складають 5, а утримання комірника – 4 гр. од. за одиницю часу. За період часу Т в систему надходить T заявок, тобто 1,445 T заявок.

Витрати внаслідок простою робітників при різному числі комір­ників, витрати на заробітну плату комірників, а також сумарні витрати і втрати наведені в табл. 1.12.

Таблиця 1.12

Дата добавления: 2014-12-26