
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Гіпербола
|
|
|
|
Еліпс
Еліпсом називається множина всіх точок площини, сума відстаней від кожної з яких до двох даних точок 
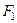 и
и  цій же площині, званих фокусами еліпса, є величина постійна і більша, ніж відстань між фокусами. Канонічне рівняння еліпса:
цій же площині, званих фокусами еліпса, є величина постійна і більша, ніж відстань між фокусами. Канонічне рівняння еліпса:

 , (3)
, (3)
де  — велика піввісь,
— велика піввісь,  - Мала піввісь еліпса.
- Мала піввісь еліпса.

v Якщо  , то:
, то:
1) координати фокусів  :
:  ,
, 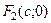 , де
, де  — половина відстані між фокусами (див. рис); числа
— половина відстані між фокусами (див. рис); числа 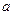 ,
,  і
і  пов'язані співвідношенням
пов'язані співвідношенням
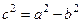 ; (4)
; (4)
2)відстань між фокусами дорівнює  ;
;
 . Форма еліпса характеризується його ексцентриситетом.
. Форма еліпса характеризується його ексцентриситетом.
Эксцентриситетом 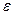 еліпса називається відношення фокусної відстані
еліпса називається відношення фокусної відстані 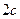 (відстані між фокусами) до великої осі:
(відстані між фокусами) до великої осі: 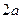 :
:
2)  (
( , т.к.
, т.к. 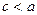 ); (5)
); (5)
 Директрисами еліпса називаються прямі и
Директрисами еліпса називаються прямі и  паралельні малої осі еліпса і віддалені від неї на відстані, рівному
паралельні малої осі еліпса і віддалені від неї на відстані, рівному 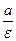 ;
;
3)  и
и  — рівняння директрис.
— рівняння директрис.
v Якщо  , то рівняння (3) визначає коло
, то рівняння (3) визначає коло  .
.
Приклад 5.2. Данно рівняння еліпса  . Знайдіть довжини його піввісь, координати фокусів, ексцентриситет еліпса.
. Знайдіть довжини його піввісь, координати фокусів, ексцентриситет еліпса.
Запишемо рівняння еліпса у вигляді (3), розділивши обидві його частини на 1176: 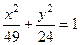 .
.
Звідси 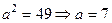 ,
,  .
.
Використовуючи співвідношення (4), знаходимо  і
і  . Отже,
. Отже,  и
и 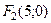 .
.
За формулою  (5) находим
(5) находим  .
.

 |
Гіперболойназивається множина всіх точок площини, модуль різниці відстаней від кожної з яких до двох заданих точок 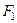 и
и  цій же площині, званих фокусами, є величина постійна, менша, ніж відстань між фокусами.
цій же площині, званих фокусами, є величина постійна, менша, ніж відстань між фокусами.
Канонічне рівняння гіперболи:

 , (6)
, (6)
де 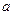 — дійсна,
— дійсна,  — уявна піввісь гіперболи. Числа
— уявна піввісь гіперболи. Числа 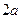 і
і  — відповідно дійсна і уявна осі гіперболи. Для гіперболи (6):
— відповідно дійсна і уявна осі гіперболи. Для гіперболи (6):  координати фокусів:
координати фокусів:  ,
, 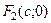 , де
, де  — половина відстані між фокусами (см. рис);
— половина відстані між фокусами (см. рис);
1) числа 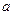 ,
,  і
і  звязані відношенням
звязані відношенням
 ; (7)
; (7)
2) відстань між фокусами дорівнює 
 ;
;
3) точки 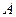 и
и  називаються вершинами гіперболи, точка
називаються вершинами гіперболи, точка  — центром гіперболи;
— центром гіперболи;
|


Эксцентриситетом 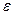 гіперболи називаеться число:
гіперболи називаеться число:
 5)
5)  (
( , т.к.
, т.к.  ). (8)
). (8)
. Прямокутник, центр якого збігається з точкою О, а сторони рівні і паралельні осях гіперболи, називається основним прямокутником гіперболи.
Діагоналі основного прямокутника гіперболи лежать на двох прямих, званих  асимптотами гіперболи они определяются уравнениями
асимптотами гіперболи они определяются уравнениями
6)  (9)
(9)
 Дві прямі
Дві прямі 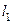 і
і  (див. мал), паралельні уявної осі гіперболи і віддалені від неї на відстані, рівному
(див. мал), паралельні уявної осі гіперболи і віддалені від неї на відстані, рівному 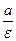 , називаються директрисами гіперболи; вони визначаються рівняннями 7)
, називаються директрисами гіперболи; вони визначаються рівняннями 7) 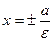 . (10)
. (10)
 Рівняння
Рівняння  або
або 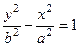 (11)
(11)
 також є рівнянням гіперболи, але дійсною віссю цієї гіперболи служить відрізок осі
також є рівнянням гіперболи, але дійсною віссю цієї гіперболи служить відрізок осі  довжини
довжини  .
.
Гіпербола, що задається рівнянням (11), називається сполученої гіперболи (6)
Пример 5.3. Складіть рівняння гіперболи, якщо її фокуси лежать на осі  і відстань між ними дорівнює 10, а довжина уявної осі дорівнює 8.
і відстань між ними дорівнює 10, а довжина уявної осі дорівнює 8.
За умовою  ,
,  ;
;  . Тоді за формулою (7) отримаємо:
. Тоді за формулою (7) отримаємо:  .
.
Тоді рівняння гіперболи:
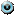

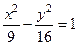 .
.
Рівняння:  ,
,  також задають гіперболу, координати центру якій задаються точкою
також задають гіперболу, координати центру якій задаються точкою  .
.

|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 800; Нарушение авторских прав?; Мы поможем в написании вашей работы!