Введение в криптографию 2 страница

Уже к началу 1930-х годов сформировались разделы математики (теория чисел, теория вероятностей и математическая статистика) являющиеся основой будущей науки – криптологии. Ключевой вехой в развитии криптографии является фундаментальный труд Клода Шеннона «Теория связи в секретных системах», написанный в форме секретного доклада в 1945 году и опубликованный в 1949 году [5,11]. В этой работе впервые был показан подход к криптографии как к математической науке. Были сформулированы ее теоретические основы и введены понятия, с объяснения которых сегодня начинается изучение криптографии.

Развитие во второй половине XX века компьютерной техники и электроники сделало возможным использование более сложных шифров. В 1960-х годах появляются первые блочные шифры, обладающие большей криптостойкостью, чем электромеханические машины. В 1976 году в США принимается государственный стандарт шифрования – DES (Data Encryption Standart), являющийся первым в мире открыто опубликованным стандартом шифрования. На основе используемой в системе DES сети Хорста Фейстеля разработаны множество других криптосистем: российский стандарт ГОСТ 28147-89, криптосистема TEA (Tiny Encryption Algorithm), Twofish, IDEA (International Data Encryption Algorithm).

В 1975 году публикуется работа Уитфилда Диффи и Мартина Хеллмана «Новые направления в криптографии» [2,8,10,11]. Данная работа открыла новую область криптографии, теперь называемую криптографией с открытым ключом. Хотя работа У. Диффи и М. Хеллмана создала большой теоретический задел для открытой криптографии, первой реальной криптосистемой с открытым ключом считают криптосистему RSA, названную по имени авторов - Рона Ривеста, Ади Шамира и Леонарда Адлемана. В настоящее время существует большое разнообразие криптосистем с открытым ключом, некоторые из которых являются национальными стандартами шифрования.

Таким образом, используя в качестве критерия периодизации технологические характеристики методов шифрования, историю криптографии можно разделить на следующие периоды.

1. Первый период (приблизительно с 3 тысячелетия до н.э. до XV века) характеризуется господством моноалфавитных шифров.

2. Второй период (с XV века по XX век) ознаменован введением многоалфавитных шифров.

3. Третий период (с начала и до середины XX века) характеризуется внедрением электромеханических шифровальных машин.

4. Четвертый период (с середины до 70-х годов XX века) – период перехода к математической криптографии.

5. Современный период (с конца 70-х годов XX века по настоящее время) характеризуется широким использованием криптографии частными лицами коммерческими организациями, что связано с развитием нового направления в криптографии – криптографии с открытым ключом.

1.3. Модели источников открытых текстов

Открытый текст, также как и криптограмма, представляет собой последовательность символов, взятых из конечного набора, называемого алфавитом 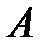. Элемент алфавита называется буквой, а число символов алфавита определяет его мощность 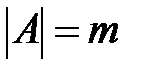. Например, алфавит простых букв английского языка имеет мощность 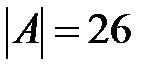, а алфавит английского языка, состоящий из прописных, строчных букв, цифр, а также знаков препинания и пробела имеет мощность 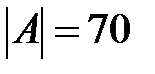. Широко используемыми алфавитами, элементы которых есть двоичные векторы, являются коды ASCII и МТК-2.

Всякий открытый текст, записанный в некотором алфавите, имеет длину 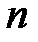, равную числу букв в соответствующей записи. Последовательность 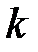соседних букв текста, при 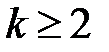называется 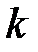- граммой, а при 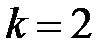- биграммой. Помимо исходного алфавита, часто рассматриваются производные из него алфавиты, представляющие наборы всевозможных 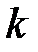-граммисходного алфавита. Таким образом, каждый открытый текст характеризуется: набором используемых алфавитов; длиной текста; тематикой открытых текстов.

Модели открытых текстов разделяются на два класса: детерминированные и вероятностные [11].

1.3.1 Детерминированные модели

Источники открытых сообщений (ИОС) достаточно многообразны. В качестве ИОС рассматривать можно отдельного человека или группу людей, пункты телеграфной и телефонной сети и т.д. Каждый ИОС порождает тексты в соответствии с правилами грамматики используемого языка, что находит отражение и в статистических характеристиках открытых текстов. Всякий ИОС можно характеризовать разбиением множества 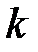-грамм на допустимые (встречающиеся в текстах) и запрещенные (не встречающиеся в текстах). Например, в русском языке буквы Ь и Ъ никогда не соседствуют друг с другом, и не следуют за гласными буквами. Разбиение множества 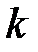-грамм на допустимые и запрещенные определяет детерминированную модель. В детерминированной модели открытый текст рассматривается как последовательность букв некоторого алфавита, не содержащий запрещенных 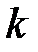-грамм. Необходимо отметить, что разделение на допустимые и запрещенные 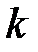-граммы весьма условно в силу динамичности языка, его способности к развитию. Кроме этого, разделение на допустимые и запрещенные 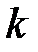-граммы характеризует не только язык, но и отдельный источник сообщений.

1.3.2 Вероятностные модели

В вероятностных моделях ИОС рассматривается как источник случайных последовательностей. Пусть ИОС генерирует в заданном алфавите 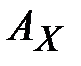текст конечной или бесконечной длины. При этом можно считать, что источник генерирует конечную или бесконечную последовательность случайных букв 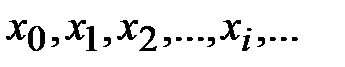, принимающих значение в .

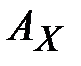Вероятность случайного сообщения 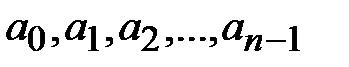определяется как вероятность последовательности событий:

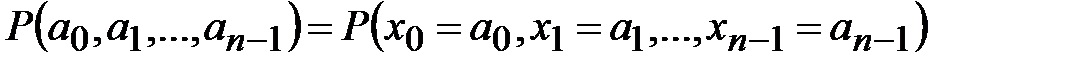. (1.1)

Множество случайных текстов образует вероятностное пространство, если выполнены условия:

1) 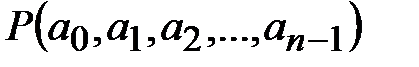для любого случайного сообщения ;

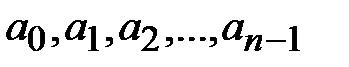2) ;

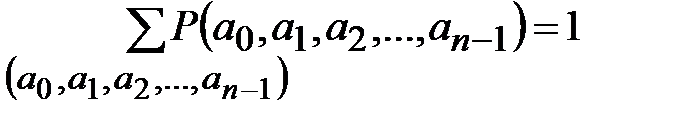3) для любого случайного сообщения 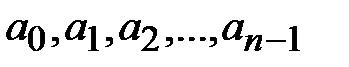и любого 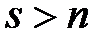справедливо 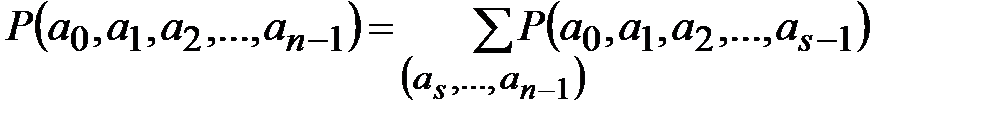, то есть вероятность всех продолжений текста длины 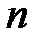есть сумма вероятностей этого сообщения до длины 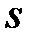. Текст, порождаемый таким ИОС, является вероятностным аналогом языка. Задавая определенное вероятностное распределение на множестве открытых текстов задается соответствующая модель ИОС.

Различают стационарные и нестационарные ИОС [11]. Для стационарных моделей характерно то, что вероятность появления буквы (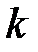 -граммы) не зависит от места в открытом тексте. Рассмотрим наиболее используемые стационарные модели ИОС.

Стационарный источник независимых символов алфавита. В этой модели предполагается, что вероятности сообщений полностью определяются вероятностями использования отдельных букв алфавита в тексте:

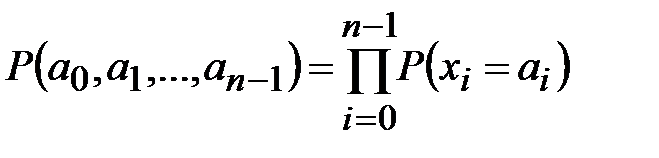, (1.2)

где для всех 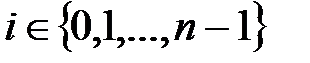и любого , .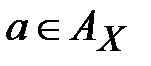

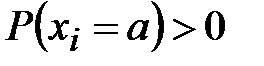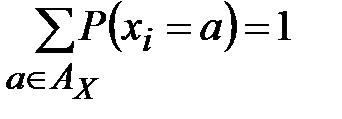Открытый текст такого источника является реализацией последовательности независимых испытаний в полиномиальной вероятностной схеме с числом исходов равным 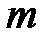. Множество исходов взаимно-однозначно соответствует множеству всех букв алфавита. Данная модель позволяет разделить буквы алфавита на классы высокой, средней и низкой частоты использования. Например, в русском языке редкими буквами являются Ф, Э, Щ, Ц, Х. В криптографии существует мнемоническое правило, которое позволяет запомнить десять наиболее часто встречаемых букв в русском языке – СЕНОВАЛИТР, причем буквы располагаются не в соответствии с частотой их использования. Необходимо заметить, что частота встречаемости букв в тексте зависит от тематики текста. Так для литературных произведений и научно-технических текстов значение частот встречаемости букв будет различным. Например, в математических текстах частота встречаемости буквы Ф будет выше, чем в литературных произведениях. Таким образом, частотная диаграмма является достаточно устойчивой характеристикой открытого текста.

Рассмотренная модель удобна для практического использования, в то же время некоторые свойства модели противоречат свойствам языка. В частности, согласной этой модели любая 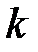-грамма имеет ненулевую вероятность использования. Вышесказанное не позволяет применять данную модель для дешифрирования широкого класса криптосистем.

Стационарный источник независимых биграмм. Эта модель более громоздка, но точнее отражает свойства языка. Открытый текст такого ИОС является реализацией последовательности независимых испытаний в полиномиальной вероятностной схеме с числом исходов, равным 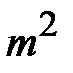.Множество исходов соответствует множеству всех биграмм алфавита. Модель характеризуется равенством:

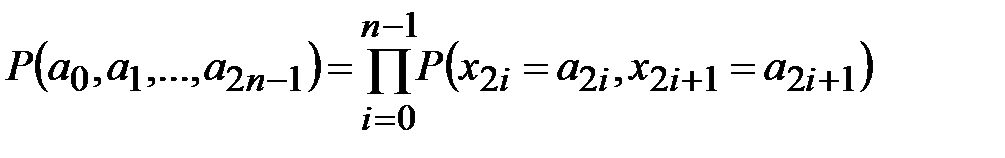, (1.3)

где для всех 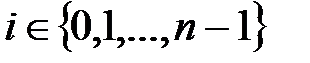и любых , .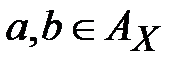

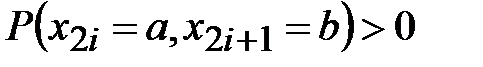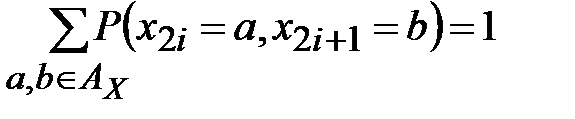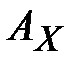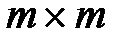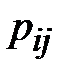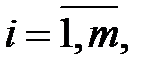
В качестве оценок вероятностей биграмм используются относительные частоты их появления, которые вычисляются экспериментально на большом текстовом материале. Вероятности биграмм в алфавите могут быть сведены в матрицу размера , где , 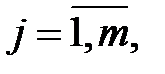есть вероятность размещения биграммы 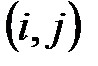на случайно выбранной позиции в открытом тексте. Например, в английском языке все биграммы 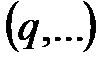за исключением 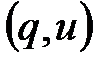имеют нулевую вероятность. Данная модель точнее по сравнению с предыдущей отражает особенности языка и ИОС. В то же время моделью игнорируются зависимости между соседними биграммами. В меньшей степени указанный недостаток присущ следующей модели.

Стационарный источник марковски зависимых букв. Открытый текст такого ИОС является реализацией последовательности испытаний, связанных простой однородной цепью Маркова с 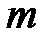состояниями. Данная модель полностью определяется матрицей вероятностей переходов 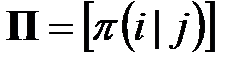, , 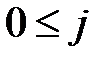, 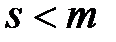вектором 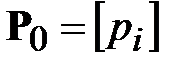, 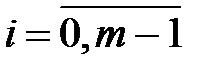начального распределения вероятностей, где 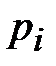- вероятность 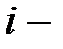й буквы на первой позиции в открытом тексте.

Вероятность случайного сообщения 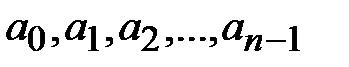определяется выражением:

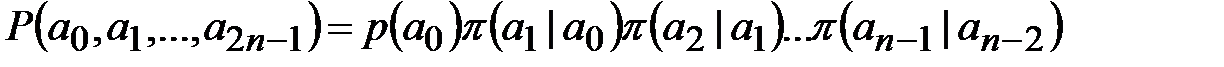. (1.4)

Согласно данной модели всякое сообщение, содержащее на какой-либо позиции запрещенную биграмму, имеет нулевую вероятность. На основании рассмотренных моделей можно предположить их усложнения в направлении увеличения глубины зависимости вероятности очередной буквы текста от значений вероятности нескольких предыдущих букв. Здесь можно выделить два типа моделей ИОС: стационарный источник независимых 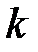-грамм и стационарный источник зависимых 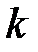-грамм.

Для моделей первого типа всякое сообщение является реализацией последовательности испытаний в полиномиальной вероятностной схеме с числом исходов, равным 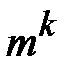. Эти модели адекватно отражают межсимвольные зависимости внутри каждой 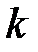-граммы, но игнорируют межсимвольные зависимости соседних 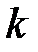-грамм. Чем больше 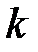, тем, с одной стороны, точнее рассматриваемые модели отражают свойства языков и ИОС и, с дугой стороны, тем они более громоздки и трудоемки и трудоемки в применении.

Модели второго типа способны учесть межсимвольные зависимости соседних 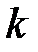-грамм, однако они еще более громоздки, чем модели первого типа. Так, если модели первого типа описываются 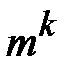-мерной матрицей вероятностей, то модели второго типа – матрицей размерностью и 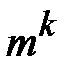–мерным вектором начального распределения.

Выбор конкретной модели носит компромиссный характер и осуществляется с учетом свойств конкретной криптосистемы.

В нестационарных моделях вероятности появления 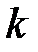-грамм в тексте зависят от их места в тексте. Нестационарные модели можно рассматривать, как уточнение стационарных, в которых в той или иной мере учтена структура сообщения.

1.4. Модели шифров

Одним из первых ввел и исследовал математическую модель шифра К. Шеннон [1,5,12]. Пусть 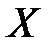, , 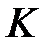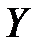некоторые конечные множества, соответственно множество открытых текстов, множество ключей и множество криптограмм. Задано отображение:

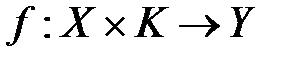. (1.5)

Введенная тройка множеств 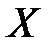, , 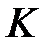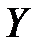с функцией (1.5) представляет собой алгебраическую модель шифра. При этом должны выполняться следующие условия:

- функция (1.5) сюрьективна (осуществляет отображение на );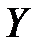

- для любого 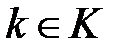функция (1.5) инъективна (образы двух различных элементов различны);

- .

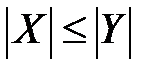Выражение (1.5) представляет собой выражение шифрования. Выражение расшифрования имеет вид:

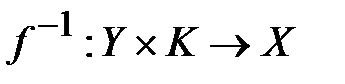. (1.6)

Требование инъективности отображения (1.5) равносильно требованию возможности однозначного расшифрования криптограммы. Требование сюрьективности отображения (1.5) не играет существенной роли и оно обычно вводится для устранения некоторых технических, с точки зрения математики, неудобств, т.е. для упрощения изложения. Алгебраическая модель шифра отражает лишь функциональные свойства шифрования и расшифрования в классических (симметричных) системах шифрования. В этой модели открытый текст (криптограмма) является лишь элементом абстрактного множества 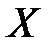(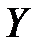), не учитывающий особенностей языка и вообще говоря, не являющийся текстом в его привычном понимании.

Достаточно часто выражения для шифрования и расшифрования записываются в операторной форме:

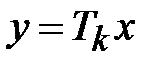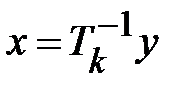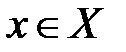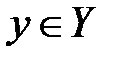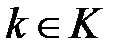, , , , , (1.7)

где 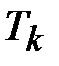, 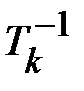- операторы шифрования и расшифрования, соответственно, на ключе .

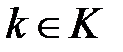Использование операторной формы записи позволяет определить операторы комбинирования криптосистем. Наиболее часто на практике используется два типа оператора комбинирования криптосистем: взвешенное суммирование криптосистем; произведение криптосистем [1].

Взвешенной суммой криптосистем называется такая криптосистема, которая образована «взвешенным» суммирование нескольких криптосистем:

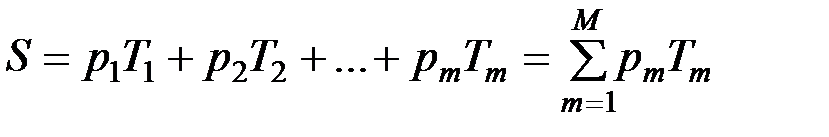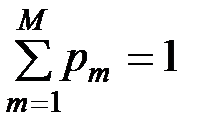, , (1.8)

где 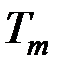- криптографическое преобразование 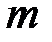-й криптосистемы; 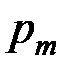- вероятность выбора 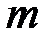-й криптосистемы.

Операция, выраженная приведенной выше формулой, состоит, во-первых, из предварительного выбора криптосистем 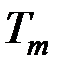с вероятностями 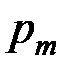. Этот выбор по сути является частью ключа криптосистемы 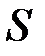. После того как этот выбор сделан, криптосистемы 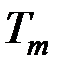применяются в соответствии с их алгоритмами. Полный ключ криптосистемы 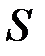должен указывать, какая из криптосистем 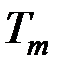выбрана и с каким ключом используется выбранная система.

На рис. 1.5 представлена обобщенная структурная схема комбинированной криптосистемы 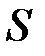, образованной взвешенным суммированием криптосистем .

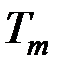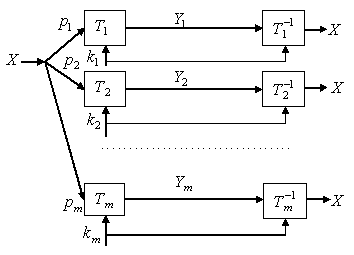
Рис. 1.5. Взвешенная сумма криптосистем

Второй способ комбинирования криптосистем заключается в образовании произведения криптосистем. Произведением криптосистем называется такая криптосистема 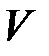, для которой выполняется равенство:

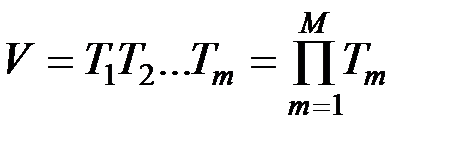. (1.9)

Строго говоря, данное выражение справедливо только в том случае, если область определения (пространство открытых текстов) криптосистемы 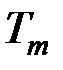отождествляется с областью значений (пространством криптограмм) системы 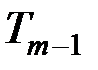. Тогда можно применить сначала криптосистему 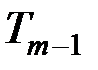, а затем криптосистему 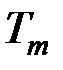к результату шифрования (см. рис. 1.6). Ключ криптосистемы 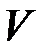состоит как из ключей криптосистем 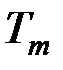. Произведение шифров используется достаточно часто; например, после подстановки применяют перестановку или после перестановки – шифр Виженера; или же применяют шифр перестановки к тексту, а затем зашифровывают результат с помощью шифра замены, дробного шифра и т.д.

Необходимо заметить, что произведение криптосистем, вообще говоря, некоммутативно, т.е. не всегда 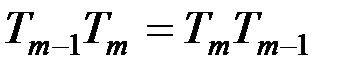, хотя в частных случаях (таких, как подстановка и перестановка) коммутативность имеет место. Произведение криптосистем представляет собой ассоциативную операцию, т.к. оно по определению ассоциативно, т.е. .

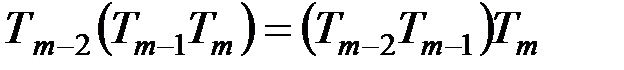Рис. 1.6. Произведение криптосистем

Важным свойством криптосистем является транзитивность. Транзитивными криптосистемами называют криптосистемы, для которых выражение (1.5) разрешимо относительно 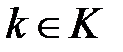при любых парах 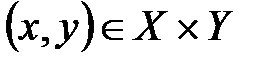. Транзитивные шифры для которых 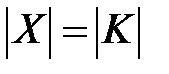называют минимальными. Криптосистемы, у которых пространства 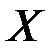и 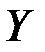можно отождествить (этот случай является очень частым) называются эндоморфными. Эндоморфная криптосистема может быть представлена как:

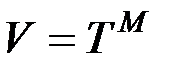. (1.10)

Криптосистема 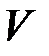, для которой справедливо соотношение:

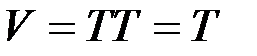. (1.11)

называется идемпотентной. Например, простая подстановка, шифр Виженера с периодом 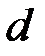являются идемпотентными. Две криптосистемы называются эквивалентными, если обе они произвольный открытый текст переводят в одну и ту же криптограмму.

Одно из важнейших предположений К.Шеннона при исследовании криптосистем состояло в том, что каждому возможному передаваемому сообщению (открытому тексту) соответствует априорная вероятность, определяемая вероятностным процессом получения сообщения. Аналогично, имеется и априорная вероятность использования различных ключей. Эти вероятностные распределения на множестве открытых текстов, и множестве ключей характеризуют априорные знания противника относительно используемого шифра. При этом К.Шеннон предполагал, что сам шифр известен противнику.

Вероятностной моделью шифра называется его алгебраическая модель с заданными дискретными независимыми вероятностными распределениями 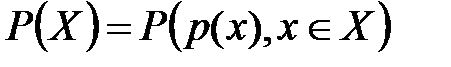, 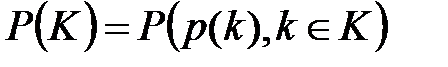на множествах 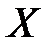и .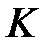

Естественно, вероятностные распределения на 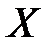и 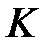индуцируют вероятностное распределение 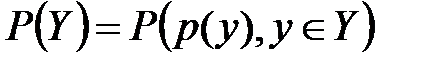на 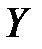, совместные распределения 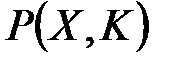, , 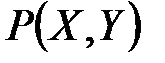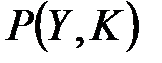и условные распределения 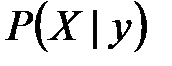и .

И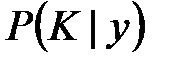спользуя вероятностную модель шифра К.Шеннон впервые сформулировал понятие совершенно стойкого шифра, которое легло в основу теории стойкости криптосистем [5,13].

Дата добавления: 2014-12-26