Методы криптоанализа симметричных криптосистем 2 страница

(3.17)

Тогда:

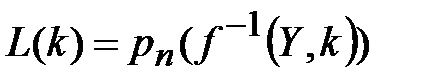. (3.18)

Функция правдоподобия 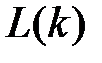позволяет судить, насколько правдоподобно получить криптограмму при условии, что ключ равен 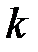. На практике оперируют не самой функцией правдоподобия, а ее монотонным преобразованием, в частности логарифмом функции правдоподобия:

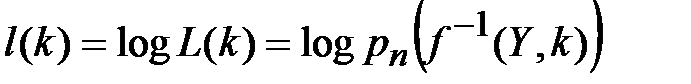. (3.19)

Для получения оценочного значения ключа требуется отыскать такое его значение, которое максимизирует значение функционала:

. (3.20)

Рассмотрим применение частотного метода криптоанализа к криптосистеме Цезаря для двух случаев:

1) источник открытых сообщений представляет собой стационарный источник дискретных сообщений без памяти;

2) источник открытых сообщений представляет собой однородную цепь Маркова.

Случай 1. Стационарный источник дискретных сообщений без памяти. Открытый текст представляется в виде:

. (3.21)

Введем величину, имеющую смысл частоты встречаемости символа 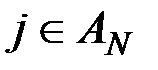в :

, (3.22)

где 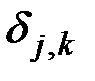- символ Кронекера, 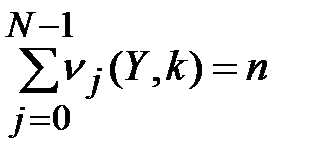- условие нормировки.

Совместное n -мерное дискретное распределение вероятностей исходного текста имеет вид:

, (3.23)

где 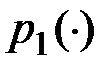- распределение вероятностей для одного символа алфавита .

Тогда логарифм функционала правдоподобия имеет вид:

(3.24)

Тогда:

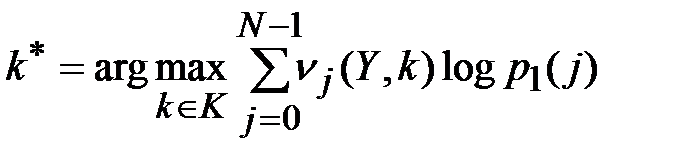. (3.25)

Например, для криптосистемы Цезаря выражение (3.20) будет иметь вид:

. (3.26)

Случай 2. Марковский источник открытых сообщений (однородная цепь Маркова). Открытый текст представляет собой реализацию однородной цепи Маркова, которая задана:

- матрицей вероятностей переходов ;

- вектором начального распределения вероятностей .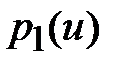

Введем в рассмотрение выражение для частот встречаемости биграмм :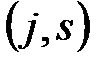

, (3.27)

При этом должно выполняться условие нормировки 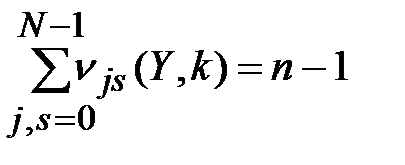. Оценка ключа будет определяться в соответствии с выражением:

. (3.28)

Например, для криптосистемы Цезаря оценка ключа будет иметь вид:

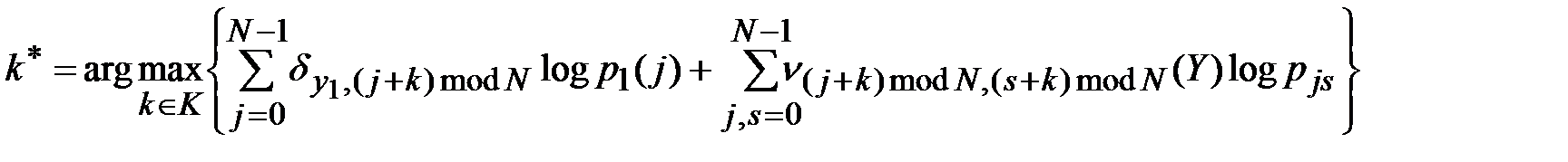Точность решения задачи криптоанализа частотным методом, т.е. точность оценки характеризуется вероятностью ошибки:

. (3.29)

Алгоритм криптоанализа является состоятельным, если при увеличении длины криптограммы 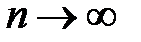вероятность ошибки стремиться к нулю . Более сложные выражения для оценки ключа 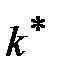получаются, если снять допущение о детерминированности ключа. Алгоритм криптоанализа в этом случае базируется на байесовском методе теории статистических решений и подробно описан в [10].

3.5. Линейный криптоанализ

Метод линейного криптоанализа разработан в 1993 году японским криптологом Митсуру Матсуи. В первоначальном виде этот метод сформулирован применительно к криптоанализу криптосистемы DES. В настоящее время создаются новые модификации этого метода [10].

Идея метода линейного криптоанализа основана на том, что существует возможность заменить нелинейную функцию криптографического преобразования ее линейным аналогом. Линейный криптоанализ базируется на знании криптоаналитиком пар «открытый текст - криптограмма», а также алгоритма шифрования. Будем считать, что при генерации исходного текста 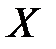случайные биты независимы и равновероятны 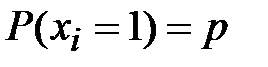, , 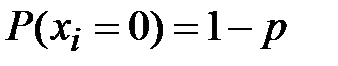. Линейным статистически аналогом (или приближенным линейным аналогом) называется:

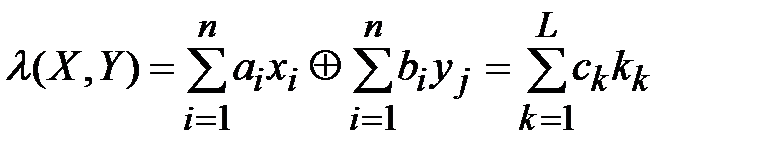, (3.30)

если вероятность 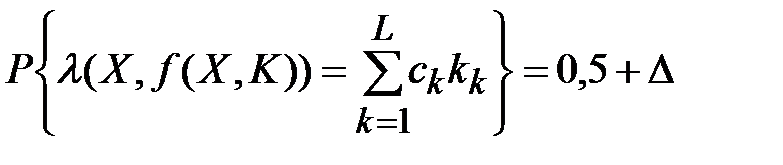. Величина 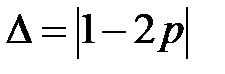называется эффективностью линейного аналога, а коэффициенты 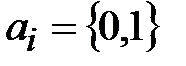, , 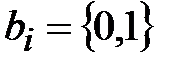- параметрами линейного аналога. По существу характеризует степень линейности функции криптографического преобразования и имеет максимальное значение .

При применении метода линейного криптоанализа решаются две взаимосвязанные задачи [4,10]:

1) нахождение эффективного линейного статистического аналога и вычисление его вероятности;

2) определение ключа (или нескольких бит ключа) с использованием эффективного линейного статистического аналога.

Практическая реализация метода линейного криптоанализа связана с реализацией следующих последовательных шагов.

1. Тщательно анализируется криптографическая функция и определяется множество линейных статистических аналогов. На этом шаге в первую очередь анализируются S-блоки функции усложнения . Для этого необходимо для каждого S-блока сформировать таблицы значений 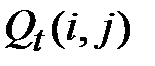, где: 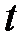- номер S-блока. Значение представляет собой количество совпадений суммы по mod2 некоторых битов входных данных с суммой по mod2 некоторых битов выходных данных. В ходе анализа прослеживаются все возможные комбинации двоичных векторов 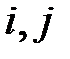. Каждая пара векторов используется в качестве маски, которая накладывается на возможные пары «вход-выход» S-блока. Эти маски указывают на биты входа и выхода, которые необходимо сложить по mod2, а затем сравнить полученные результаты. Далее проводится анализ полученных таблиц 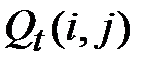и отыскивается такие значения , для которых выполняется условие

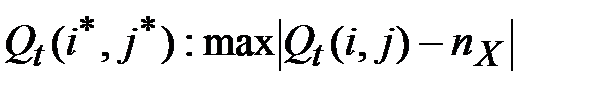, (3.31)

где 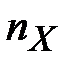- длина подблока.

В соответствии с полученной парой 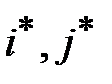, и учитывая в схеме алгоритма шифрования перестановки и сложение по mod2, формируется эффективный линейный статистический аналог

, при 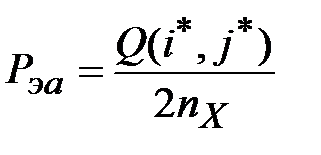. (3.32)

Как правило, формируются несколько линейных аналогов (один из них эффективный) для которых значения вероятностей близки.

2. Генерируется множество независимых исходных текстов и регистрируются соответствующие им криптограммы .

3. Для каждой пары 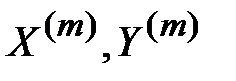, 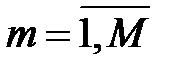вычисляется значение левой части эффективного линейного статистического аналога:

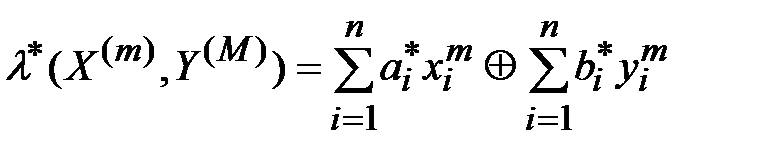. (3.33)

4. Определяется частота получения «1» при вычислении M значений (3.33):

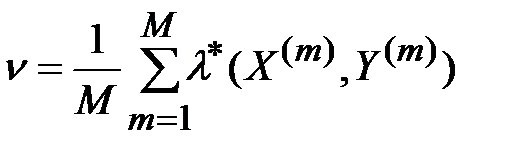, (3.34)

и строится оценка максимального правдоподобия в соответствии с правилом:

(3.35)

Вычисления на этапах 3 и 4 выполняются для всех сформированных эффективных линейных статистических аналогов.

5. Строится система линейных уравнений, причем каждое уравнение системы представляет собой равенство правой части (3.32) и соответствующего значения (3.35)

. (3.36)

Единственное решение полученной системы (3.36) используется в качестве оценки ключа . Таким образом, на шаге 1 решается первая задача линейного криптоанализа, а шаги 2-5 обеспечивают решение второй задачи.

Рассмотрим пример реализации алгоритма линейного криптоанализа на базе криптосистемы S-DES, подробно рассмотренной в [4]. Криптосистема S-DES разработана для изучения свойств криптосистем, основанных на схеме Фейстеля. Алгоритм шифрования по своей структуре аналогичен алгоритму DES. Отличие состоит в следующем:

- алгоритм имеет два раунда шифрования;

- алгоритм оперирует 8 битными входными блоками;

- функция усложнения включает два блока замены;

- основной ключ шифра 10 битный, а раундовые ключи 8 битные.

Таблицы замен и перестановок приведены в [4]. Для простоты, но, не нарушая общности, будем считать, что шифрование производилось одним раундом.

В соответствии с алгоритмом линейного криптоанализа вначале проводиться анализ блоков замены (см. табл. 3.1, табл. 3.2) функции усложнения.

Таблица 3.1. Блок замены 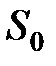Таблица 3.2. Блок замены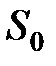

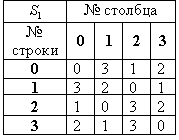
Результаты анализа блока 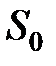и блока приведены в табл. 3.3 и 3.4.

Таблица 3.3. Анализ блока 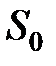Таблица 3.4. Анализ блока

i

Значение j

i

Значение j

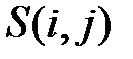
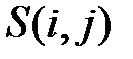
Итак, в соответствии с табл. 3.3, можно выделить четыре эффективных линейных статистических аналога и составить первые четыре наиболее эффективных линейных уравнения, соответствующие парам: (i, j) – , , 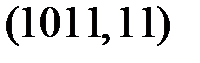, 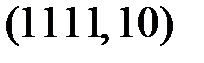. В соответствии с табл. 3.4 можно выделить семь эффективных линейных статистических аналогов и составить семь наиболее эффективных линейных уравнений, соответствующие парам: (i, j) – , , , , 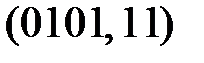, , 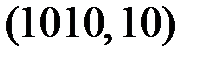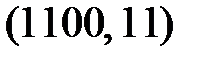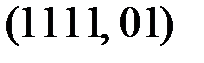. Следует отметить, что одно из уравнений будет более эффективным, однако его не достаточно для нахождения битов ключа.

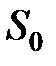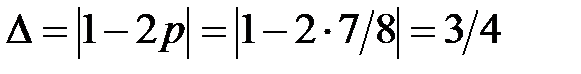Рассмотрим первую пару блока . Очевидно, что выполняется с вероятностью , а соответственно . Тогда, в соответствии с (3.32) можно записать первое линейное уравнение для блока замены :

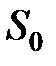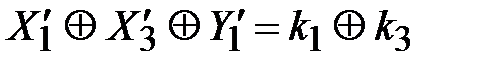. (3.37)

Повторяя подобные рассуждения аналогично можно записать и другие линейные уравнения для блока :

,

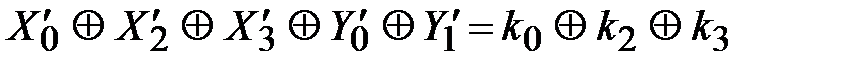, (3.38)

.

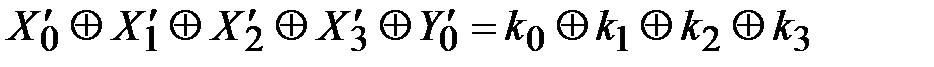и блока :

,

,

,

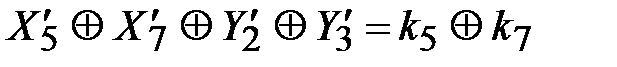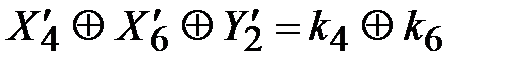, (3.39)

,

,

.

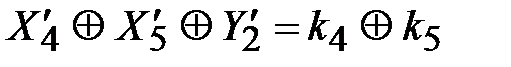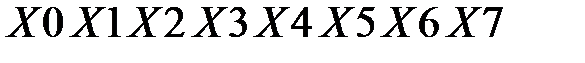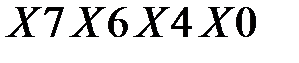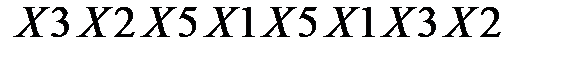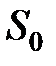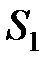Представим исходный текст, как . Затем выполняется начальная перестановка IP [4]. После перестановки получаем , далее текст разбивается на левую часть и правую часть . Правая часть подвергается перестановке с расширением Е [4]. В результате получается следующий результат - , который складывается с битами раундового ключа . На блок подаем , на блок подаем 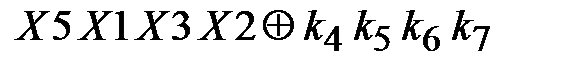. Представим входные биты блоков замены в следующем виде. Для блока 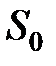справедливы зависимости:

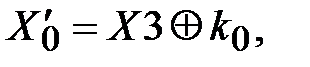
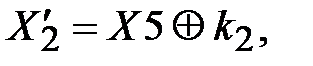
. (3.40)

Для блока 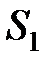справедливы зависимости:

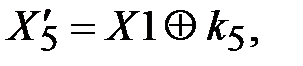
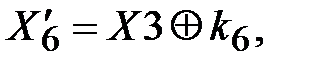
. (3.41)

Пусть криптограмма имеет вид . Вид информационного блока до конечной перестановки (обратной начальной) имеет вид Разбиваем данный блок на левую часть и правую часть 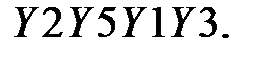Правая часть 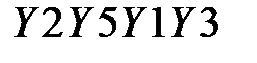получается в результате сложения по модулю 2 левой части исходного текста после перестановки IP 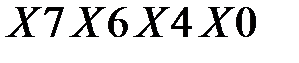с текстом прошедшим функцию усложнения. На выходе блоков замены функции усложнения имеем - . После перестановки Р получаем 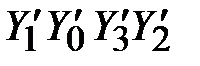. В результате можно записать:

, , , (3.42)

Теперь подставим линейные уравнения (3.40) – (3.42) в уравнения (3.38) и (3.39) и получим уравнения линейных статистических аналогов. Полученные результаты сведем в табл. 3.5.

На этом первый этап алгоритма линейного криптоанализа закончен. Выбрав в качестве ключа шифрования 0010001111 реализуем второй, третий и четвертый этапы. Сформировав набор пар «открытый текст – криптограмма», используя 0010001111, на основании выражения (3.33) вычислим левые части линейных эффективных аналогов.

Таблица 3.5. Линейные статистические аналоги

№ блока	Линейные уравнения	р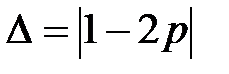

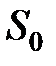
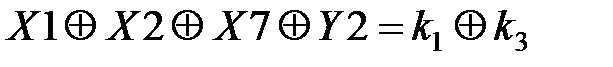
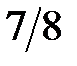
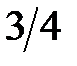
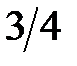
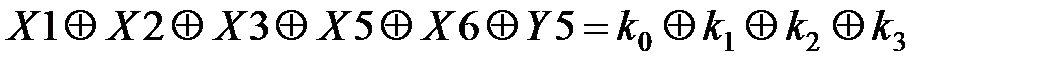
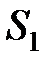
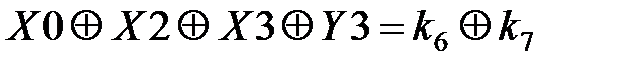
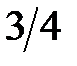
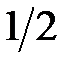
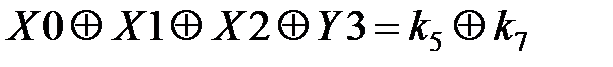
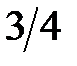
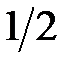
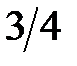
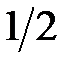
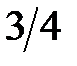
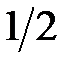
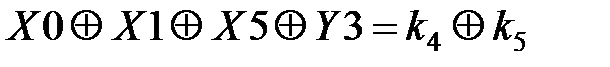
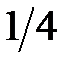
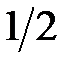
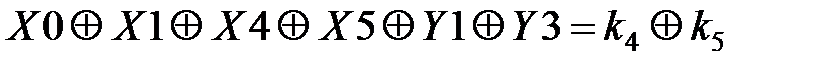
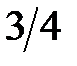
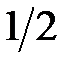
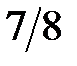
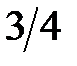
В результате получаем систему уравнений (пятый этап):

, , , ,

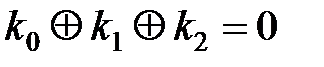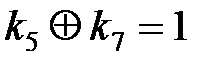, , , , , (3.43)

.

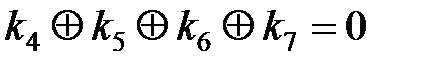Решение системы уравнений (3.43) имеет вид:

, , , ,

, , , ,

, , , ,

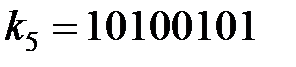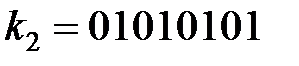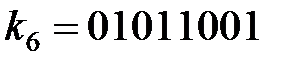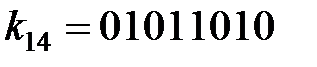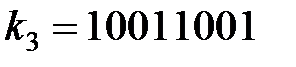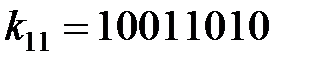Дата добавления: 2014-12-26