Симметричные криптосистемы и их свойства 1 страница

2.1. Шифры замены

Пусть имеется открытое сообщение 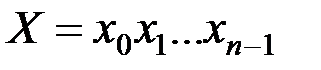длины 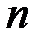в алфавите 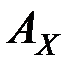и правило замены 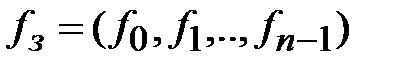, тогда применение этого криптографического преобразования к открытому сообщению дает криптограмму 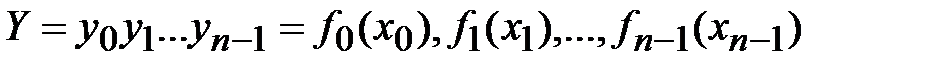. Семейство криптографических преобразований 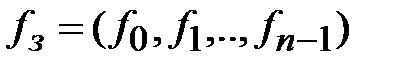называется шифром замены.

В зависимости от вида криптографической функции 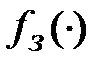шифры замены делятся на шифры моноалфавитной замены и шифры многоалфавитной замены. Моноалфавитные замены – наиболее простой вид преобразований, заключающийся в замене по определенному правилу букв исходного сообщения на другие буквы из этого же алфавита, т.е. каждая буква исходного текста преобразуется в букву криптограммы по одному и тому же закону. В случае многоалфавитной замены закон преобразования меняется от буквы к букве. Необходимо заметить, что один и тот же шифр может рассматриваться и как моно-, и как многоалфавитная замена в зависимости от определяемого алфавита. Например, замена биграмм с точки зрения обычного алфавита является моноалфавитной заменой, а с точки зрения алфавита биграмм - многоалфавитным. Рассмотрим наиболее известные шифры замены [1,3,4,8-11].

Шифр Цезаря. Процесс зашифрования исходного текста определяется выражением:

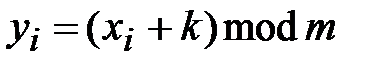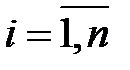, , (2.1)

где 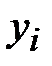- буква криптограммы, 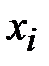- буква открытого сообщения, 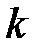-ключ шифра, 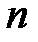- длина криптограммы (открытого текста), 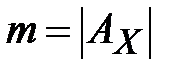- мощность алфавита 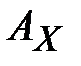. Очевидно, что выражение:

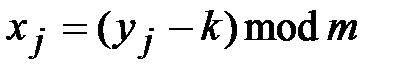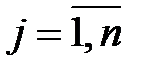, , (2.2)

определяет процесс расшифрования криптограммы.

Обобщением шифра Цезаря является аффинный шифр Цезаря, определяемый выражением:

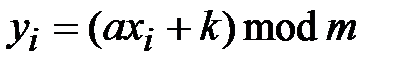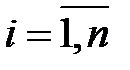, . (2.3)

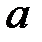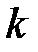Аффинный шифр Цезаря определяется двумя целыми числами и , где 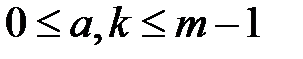,. Числа 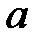и должны быть взаимно простыми. Взаимная простота 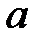и 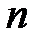необходима, т.к. в противном случае возможны отображения различных символов в один и, как следствие, неоднозначность расшифрования. Процесс расшифрования определяется выражением:

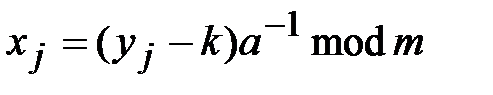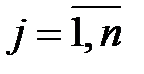, . (2.4)

Число 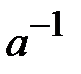является инверсией числа 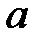по модулю 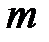при этом должно выполняться равенство .

Шифр Виженера. В шифре Виженера ключ 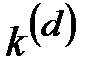задается набором из 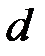символов. Такие наборы подписываются под буквами открытого текста 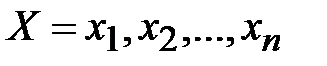, , 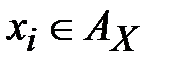до получения периодической ключевой последовательности 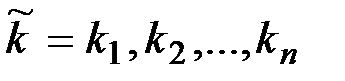, , 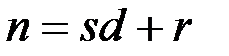где 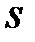- число полных периодов 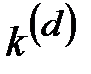, , 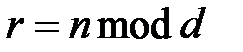а значение 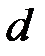определяет период ключевой последовательности. Процесс шифрования определяется выражением:

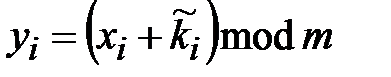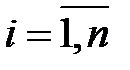, . (2.5)

При повторных операциях шифрования открытого теста шифром Виженера получаем составной шифр Виженера, который описывается выражением:

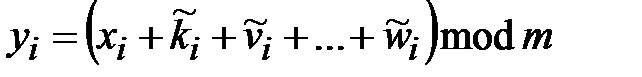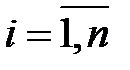, , (2.6)

где 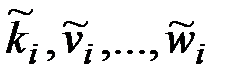- ключевые последовательности, имеющие, как правило, различные периоды. Период суммы этих ключевых последовательностей равен наименьшему общему кратному отдельных периодов. Иногда используется усложненный шифр Виженера. Усложнение заключается в «перемешивании» исходного алфавита и получении нового алфавита 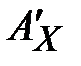, причем 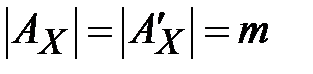. Перемешивание обычно проводится при помощи лозунга, который представляет собой слово или фразу, неповторяющиеся символы которого образуют начало алфавита. Заметим, что шифр Виженера с периодом 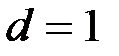представляет собой шифр Цезаря. Если же криптосистема Виженера имеет период 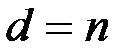, то получаем шифр гаммирования:

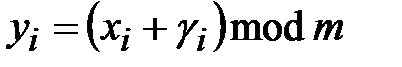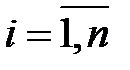, . (2.7)

В шифре гаммирования ключевая последовательность носит название гамма-последовательности . Частным случаем шифра гаммирования является шифр Вернама, который определен на алфавите .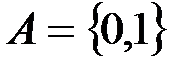

Разновидностью шифра Виженера является шифр Бофора, который определяется выражением:

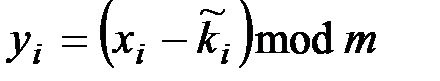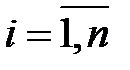, , (2.8)

т.е. шифр Бофора представляет собой «расшифрование» шифра Виженера. Шифр Бофора с периодом 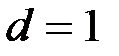представляет собой обратный шифр Цезаря. Шифр, в котором само сообщение (или его часть) или результирующая криптограмма используется в качестве ключа, называется шифром с автоключом. Шифрование в этом случае начинается с помощью «первичного ключа» и продолжается с помощью сообщения или криптограммы

Примером отечественного шифра замены является шифр простой литореи или «тарабарская грамота». Суть криптографического преобразования заключается в следующем. В таблицу из двух строк в определенном порядке записываются согласные буквы алфавита. Замена осуществляется по столбцам «сверху-вниз» или «снизу-вверх». Гласные буквы записываются без зашифрования или как говорят без «затаивания».

Шифр Плейфера. Шифр является примером шифра замены биграмм. Ключом шифра является таблица , с вписанным в нее алфавитом, размера , причем 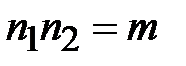. В соответствии с алгоритмом шифра Плейфера открытое сообщение разбивается на биграммы и одновременно видоизменяется так, чтобы не встречались биграммы вида 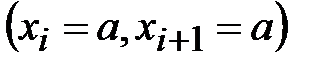. Криптографическое преобразование определяется следующим образом:

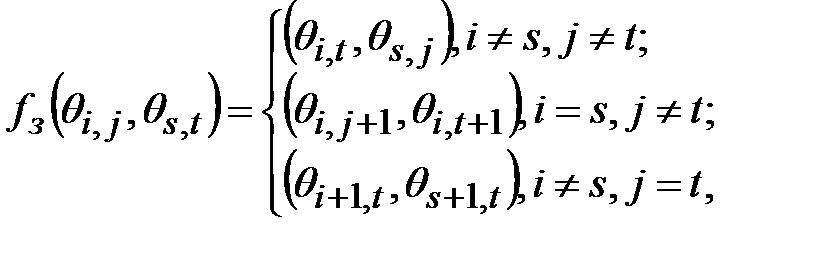(2.9)

где 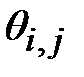- символ таблицы шифра .

2.2. Шифры перестановки

Пусть имеется открытое сообщение 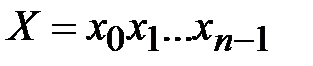длины 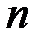в алфавите 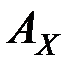и правило перестановки 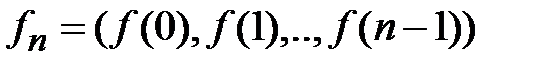, тогда применение этого криптографического преобразования к открытому сообщению дает криптограмму 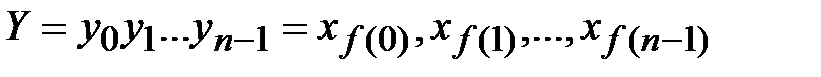. Семейство криптографических преобразований 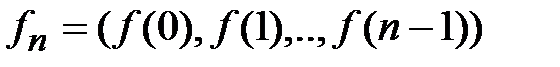называется шифром перестановки. Таким образом, перестановка заключается в переупорядочении букв открытого текста, в результате чего он становиться нечитаемым. Ключом шифра является правило перестановки. На практике при применении шифров перестановки длины открытого текста и ключа не совпадают, так как, как правило, ключ имеет фиксированную длину . В этом случае открытый текст разбивается на 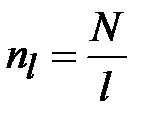отрезков длины , к каждому из которых применяется перестановка. В случае, когда открытое сообщение не может быть разделено на 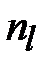равных отрезков, т.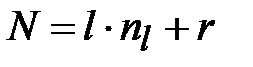е. , где 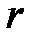- остаток, необходимо дополнить открытый текст 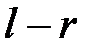произвольными символами, называемыми «пустышками». Рассмотрим наиболее известные шифры перестановки [1,3,4,8-11].

Шифр простой перестановки заключается в следующем. В соответствии с заданным правилом осуществляется перестановка букв открытого текста. Правило перестановки является ключом шифра. Как правило, длина ключа соответствует длине открытого сообщения.

Шифр перестановки с фиксированным периодом относиться к простым шифрам перестановки. Процесс шифрования заключается в следующем. Сообщение делится на блоки соответствующие заданному периоду. К каждому блоку применяется одна и та же перестановка.

Шифры маршрутной перестановки используют прямоугольную таблицу, в которую текст записывается, например, по строкам, а криптограмма считывается по определенному маршруту (по столбцам, по диагонали и т.п.). Расшифрование состоит в обратной действии, сначала по заданному маршруту заполняется таблица, а затем, например, по строкам, считывается исходный текст. Ключом таких шифров являются размеры таблицы и маршрут записи и считывания символов. Наиболее сложные маршрутные перестановки реализуются с применением гамильтоновых путей на графе (см. рис. 2.1).

Рис. 2.1. Гамильтоновы пути на графе

Шифр вертикальной перестановки является частным случаем шифра маршрутной перестановки. Шифрование заключается в записи по строкам открытого текста в таблицу, а считывание криптограммы осуществляется по столбцам.

Шифр «магический квадрат» является частным случаем шифра маршрутной перестановки и использует в качестве таблицы «магический квадрат». «Магическим квадратом» является таблица размером 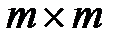, в которую вписываются числа от 1 до 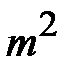так, чтобы сумма чисел по строкам, столбцам и полным диагоналям равнялась одному и тому же числу. Процесс шифрования сводился к тому, что символы открытого текста в соответствии с их порядковым номером вписывались с соответствующую этому номеру ячейку квадрата, а считывание криптограммы осуществлялось по строкам. Если в квадрате оставались пустые ячейки, то их заполняли произвольными символами. Ключом данного шифра является «магический квадрат».

Наиболее стойким из шифров перестановки с помощью таблиц является шифрование с помощью шифра Кордано, который часто называют «решеткой Кордано». Решетка используется при шифровании как ключ и представляет собой квадратную таблицу размера 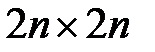( 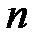- натуральное число), в которой 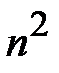всех позиций выделены для записи символов открытого текста. Эти 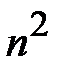позиций случайным образом более или менее равномерно распределены по площади квадрата и выбраны таким образом, что при последовательном повороте квадрата вокруг геометрического центра на 90, 180, 270 и 360 градусов вырезанные клетки последовательно покрывают все 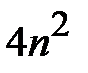клеток квадрата. При шифровании решетка Кордано накладывается на лист бумаги того же размера. В начальном угловом положении, соответствующем углу поворота 0 градусов, в клетки выделенные «окнами» решетки Кордано последовательно (по строкам слева направо, или в другом оговоренном заранее порядке) записываются первые символов открытого сообщения. Затем решетка Кордано поворачивается в угловое положение 90 градусов и вновь в клетки выделенные «окнами» последовательно записываются следующие 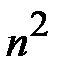символов открытого сообщения. Данная операция повторяется до полного поворота решетки вокруг своего геометрического центра. Если длина сообщения 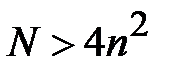, то решетка Кордано используется многократно для зашифрования всего сообщения. Криптограмма считывается с листа бумаги в оговоренном заранее порядке. Главное требование к решетке Кордано – при всех поворотах «окна» не должны попадать на одно и тоже место в квадрате, в котором образуется криптограмма. В качестве решетки может быть использован не только квадрат, но и прямоугольник. В этом случае поворот осуществляются на 180 градусов, затем решетка переворачивается оборотной стороной и после записи символов снова поворачивается на 180 градусов.

2.3. Поточные криптосистемы

Поточные криптосистемы относятся к шифрам замены, преобразующим посимвольно открытый текст в криптограмму [2,10,11]. Традиционно шифры замены строились по принципу поточного шифрования. В современных поточных криптосистемах в качестве шифруемых символов фигурируют биты или даже байты. Поточные криптосистемы разделяются на синхронные (СПК) и асинхронные или самосинхронизирующиеся (ССПК). Упрощенная структурная схема СПК представлена на рис. 2.2.

Схема СПК состоит из управляющего и шифрующего блоков. Управляющий блок генерирует управляющую последовательность 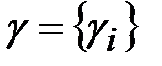, , 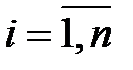которая используется для формирования шифрующих криптопреобразований 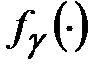. Управляющую последовательность часто называют управляющей гаммой, а управляющий блок – генератором гаммы.

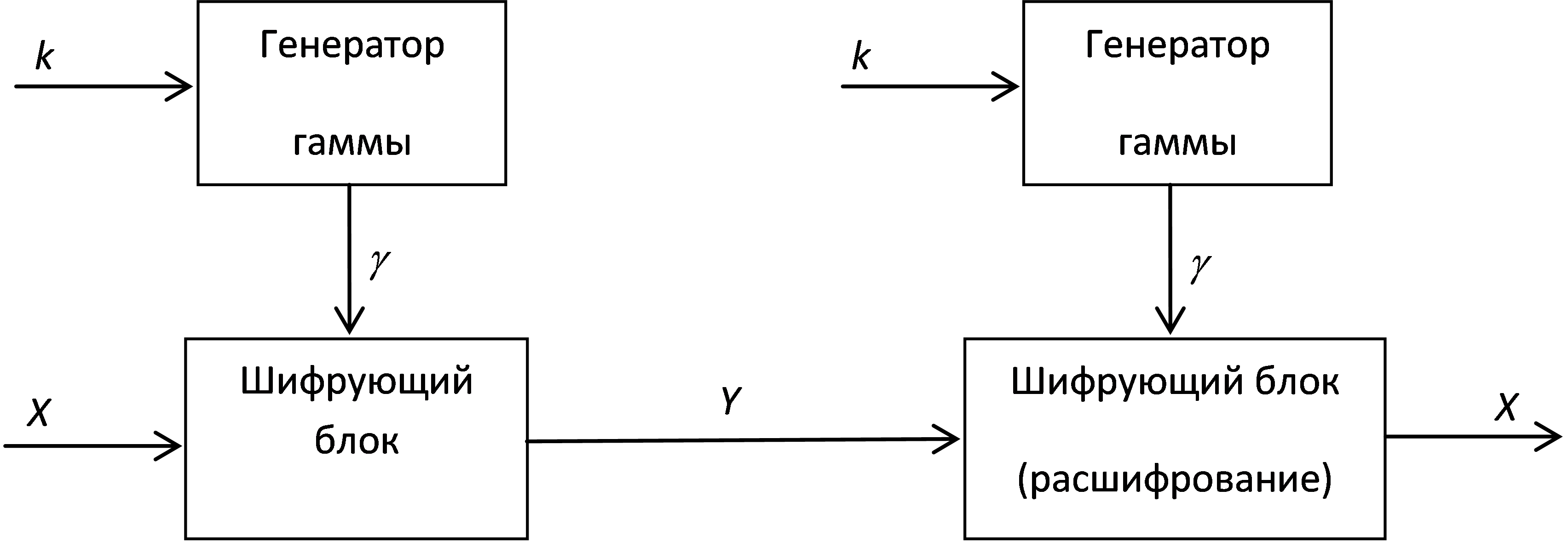
Рис. 2.2. Упрощенная структурная схема СПК

Шифрующий блок зашифровывает символ открытого текста 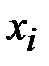в символ криптограммы 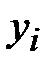с использованием криптографического преобразования 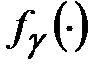. Отправитель сообщения устанавливает заранее оговоренный ключ 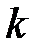генератора и, вычислив криптограмму 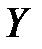, отправляет ее получателю. Для расшифрования получатель использует идентичный генератор гаммы, в который устанавливается тот же ключ 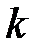. 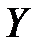Шифрующий блок получателя в режиме расшифрования вычисляет открытый текст по криптограмме используя обратное криптографическое преобразование 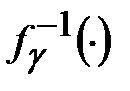. В СПК генерируемая гамма не зависит от открытого текста, т.к. генератор гаммы автономен. В связи с этим СПК функционирует исправно до тех пор, пока устройства, реализующие шифрование и расшифрование на концах линии связи, работают синхронно, то есть не имеет места расшифрование символа криптограммы 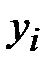с использованием символа гаммы 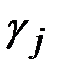, 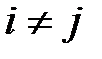. Такие нежелательные сбои, называемые рассинхронизацией, могут наступить из-за различных скоростей работы аппаратуры на приемной и передающем концах, удалении символов при передаче в канале связи и т.д. Сбои могут повлечь неправильное расшифрование всего последующего отрезка сообщения. Если такое случается отправитель и получатель должны восстановить синхронизм работы генераторов гаммы прежде, чем продолжить сеанс связи. Обычно проблемы восстановления синхронизма решаются либо с помощью повторного шифрования с реинициализацией ключа обоими абонентами (повторное использование гаммы крайне нежелательно, а в некоторых криптосистемах недопустимо), либо с помощью разбиения текста на блоки, начала и окончания которых снабжены специальными маркерами. Во втором случае рассинхронизация приводит к некорректному расшифрованию лишь до тех пор, пока получателем не будет принят один из маркеров.

К достоинствам СПК следует отнести то, что они не размножают искажений символов текста, которые довольно часто имеют место при передаче по каналам связи. Если при отправлении сообщения был искажен символ 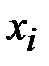или передаче по каналу связи был искажен символ 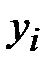, то при синхронной работе генераторов эти искажения не повлияют на правильность расшифрования всех символов, кроме 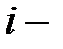го. Также СПК защищают передаваемое сообщение от несанкционированных вставок и удаления отрезков текста, так как в этих случаях произойдет рассинхронизация и «вмешательство» злоумышленника будет немедленно обнаружено. В то же время СПК не вполне защищают от умышленной подмены отрезка сообщения на другой отрезок такой же длины. Если злоумышленнику известен отрезок открытого текста, то ему не составляет труда подменить его таким отрезком, который расшифруется в требуемый фрагмент текста.

Схема ССПК также состоит из управляющего и шифрующего блоков с аналогичным функциональным назначением. Однако имеются отличия в построении управляющего блока и в схеме взаимодействия блоков. Как видно из рис. 2.3, ССПК имеет обратную связь по криптограмме, что является важным отличием ССПК. Генерируемая гамма зависит от предшествующих битов криптограммы:

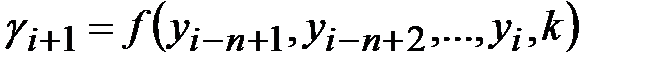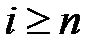, . (2.10)

Каждое внутренне состояние управляющего блока СППК (за исключением первых 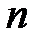состояний) заполняется 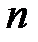предыдущими знаками криптограммы. Поэтому если 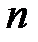следующих подряд знаков криптограммы не подвергаются искажению при передаче по линии связи, то ССПК на приемном и передающем концах устанавливаются в одинаковые внутренние состояния и, следовательно, вырабатывают при этом одинаковые символы гаммы. Т.е. происходит самосинхронизация ССПК. Как правило, каждое шифруемое сообщение начинается не с содержательного текста, а со случайного отрезка из 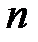символов, который шифруется, передается и затем расшифровывается. И хотя расшифрование этого отрезка реализуется некорректно в силу несовпадения начальных состояний генераторов, после передачи 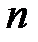начальных знаков генераторы синхронизируются. Для затруднения криптоанализа по первым 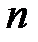символам криптограммы начальное состояние ССПК выбирается случайным образом для каждого сообщения.

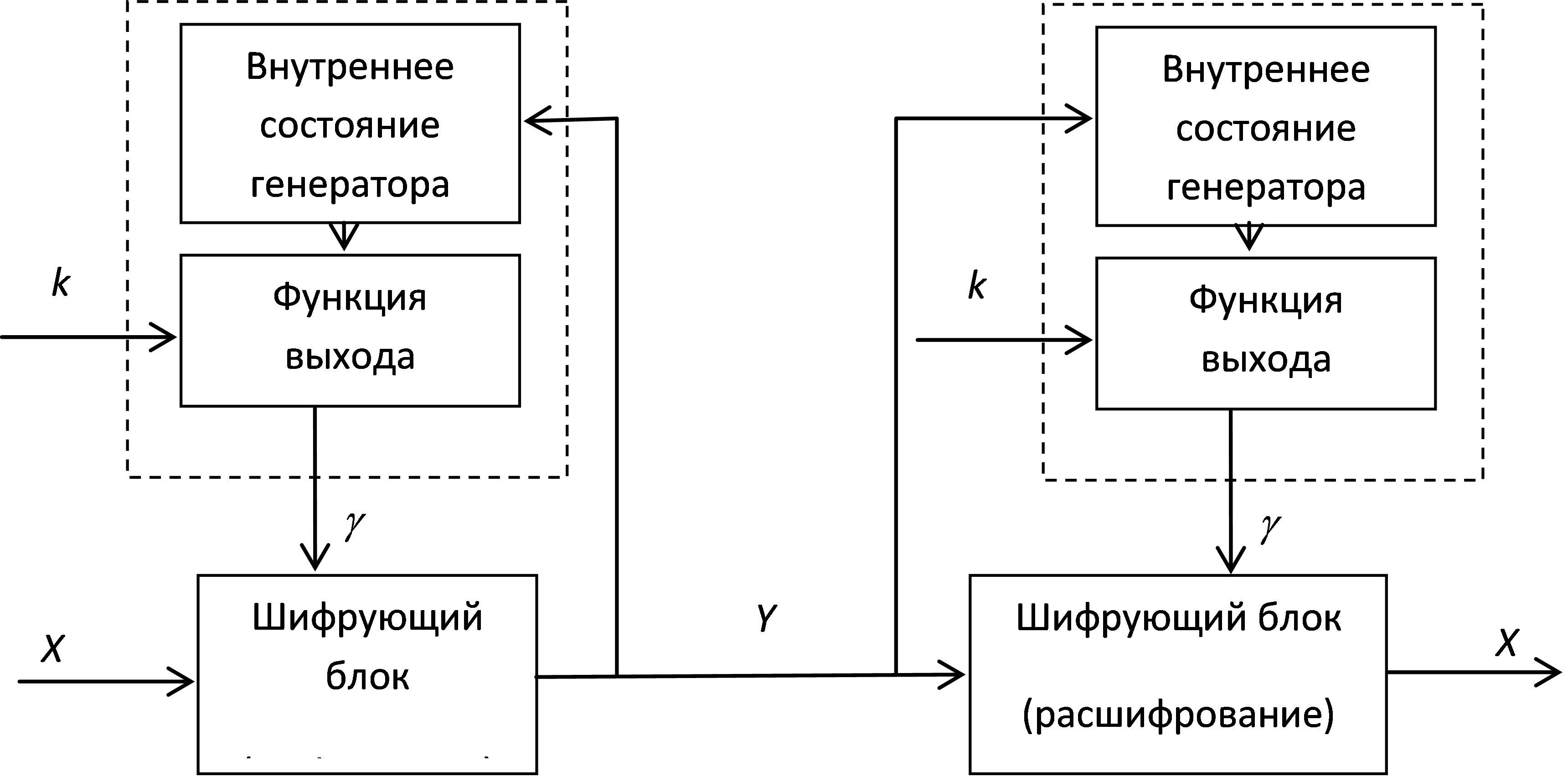
Рис. 2.3 Упрощенная структурная схема ССПК

Основным недостатком ССПК является размножение ошибок. Единичная ошибка в криптограмме порождает 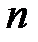ошибок в открытом тексте. Также ССПК уязвимы к имитации сообщения. Злоумышленник может записать некоторый перехваченный отрезок криптограммы и позже отправить его в адрес. После нескольких нестыковок в начале сообщения (до 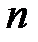символов) посланный отрезок расшифруется верно и получатель не сможет определить, что принято устаревшее сообщение. Подобная имитация невозможна, если использовать метки времени, а также менять ключи при каждом новом сообщении.

Поточные криптосистемы, как правило, являются строятся на основе шифров гаммирования. При этом различаю табличное и модульное гаммирование. Табличное гаммирование заключается в том, что криптографическое преобразование 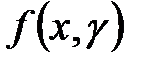представляется в виде латинского квадрата в алфавите 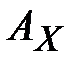. При этом, как и в случае шифра Полибия, символ криптограммы определяется на пересечении строки и столбца, которые задаются символами открытого текста и гаммы. Таким образом, шифр Полибия является примером шифра табличного гаммирования. Выражение (2.7) определяет шифр модульного гаммирования. Наиболее удобными с точки зрения практического применения являются шифры модульного гаммирования, которым соответствует уравнение:

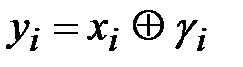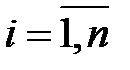, , (2.11)

где символ определяет операцию сложения по модулю 2 (операция XOR). Удобство шифров модульного гаммирования заключается в их обратимости:

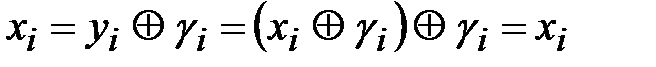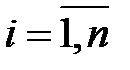, . (2.12)

Для обеспечения высокой криптографической стойкости при применении шифров гаммирования не допускается [2,11]:

- повторное использование гаммы;

- использование неравновероятной гаммы.

Рассмотрим поточные криптосистемы, которые в настоящее время находят достаточно широкое применение [2,10,11].

Поточная криптосистема RC4 (Rivest Cipher 4) был разработана Роном Ривестом в 1987 году. Эта криптосистема позволяет использовать ключи размером от 8 до 2048 бит. В RC4 для зашифрования и расшифрования применяются одни и те же действия: генерируется гамма, которая накладывается на шифруемое сообщение путем сложения по модулю 2. Криптосистема RC4 является собственностью компании RSA Data Security Inc, а ее описание никогда не было опубликовано и предоставлялось партнерам только после подписания соглашения о неразглашении. Однако в сентябре 1994 года алгоритм RC4 был анонимно опубликован. С тех пор сама криптосистема перестала быть секретом, но название RC4 остается торговой маркой. То есть, чтобы получить право заявлять, что в коммерческом программном продукте используется RC4, необходимо приобрести лицензию на этот алгоритм у RSA Data Security. Без лицензии можно утверждать лишь то, что используется алгоритм, похожий на RC4 и совпадающий с ним на всем известном множестве тестов. В связи с этим, некоторые компании не имеющие лицензии на RC4 предпочитают называть ее ARC4 (Alleged RC4). Основные преимущества криптосистемы RC4 - высокая скорость работы и переменный размер ключа. Главным фактором, способствовавшим широкому применению RC4, была простота ее аппаратной и программной реализации. Вместе с тем, RC4 довольно уязвима, если используются не случайные или связанные ключи или один ключевой поток используется дважды. Криптосистема RC4 применяется в таких продуктах, как Microsoft Office, Lotus Notes, Adobe Acrobat и др.

Поточная криптосистема VMPC (Variably Modified Permutation Composition), применяется в системах защиты информации в компьютерных сетях. Криптосистема разработана криптографом Бартошем Зольтаком в качестве улучшенного варианта криптосистемы RC4. Алгоритм VMPC строится как и любой потоковый шифр на основе параметризованного ключом генератора псевдослучайных чисел, базой которого является односторонняя необратимая функция VMPC. Основные преимущества шифра, как и RC4, - высокая скорость работы, переменный размер ключа и вектора инициализации (от 128 до 512 бит включительно), а также простота реализации.

Поточная криптосистема Rabbit – высокоскоростная криптосистема, впервые представленная в феврале 2003 года. В мае 2005, криптосистема Rabbit была отправлена на конкурс eStream, целью которого было создание европейских стандартов для поточных систем шифрования. Криптосистема Rabbit использует 128-битный ключ и 64-битный инициализирующий вектор. Криптосистема была разработан с целью использования в программном обеспечении, как обладающая высокой скоростью шифрования. Тем не менее, криптосистема также оказалась быстрой и компактной при аппаратной реализации. Основным компонентом криптосистемы является генератор битового потока, который шифрует 128 битов сообщения за итерацию. Достоинство криптосистемы в тщательном перемешивании ее внутренних состояний между двумя последовательными итерациями. Функция перемешивания полностью основана на арифметических операциях, доступных на современных процессорах. Авторы шифра предоставили полный набор технических описаний на домашней странице компании Cryptico, которая обладала патентом на криптосистему, и многие годы для ее использования в коммерческих целях требовалась лицензия. Однако, в 2008 криптосистему Rabbit разрешили использовать в любых целях бесплатно.

Дата добавления: 2014-12-26