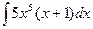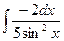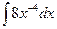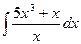КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Производные высшего порядка
|
|
|
|
Пусть мы нашли для функции y=f(x) ее производную y ¢= f ¢(x). Производная от этой производной называется производной второго порядка функции f(x), или второй производной, и обозначается:  .
.
Аналогично определяются и обозначаются:
производная третьего порядка -  ,
,
производная четвертого порядка - 
и вообще производная n-го порядка -  .
.
Частной производной от функции  по независимой переменной по независимой переменной  называется производная называется производная
 , вычисленная при постоянном , вычисленная при постоянном  .
Частной производной по y называется производная .
Частной производной по y называется производная  , вычисленная при постоянном , вычисленная при постоянном  . Для частных производных справедливы обычные правила и формулы дифференцирования.
Пример 1 . Для частных производных справедливы обычные правила и формулы дифференцирования.
Пример 1  .
Рассматривая .
Рассматривая  как постоянную величину как постоянную величину  , получим , получим  .
Рассматривая .
Рассматривая  как постоянную величину как постоянную величину  , получим , получим  .
Пример 2 .
Пример 2 
 ; ;  ; ;
 ; ;  .
Полным приращением функции .
Полным приращением функции  в точке в точке  называется разность называется разность  , где , где  и и  произвольные приращения аргументов. Функция произвольные приращения аргументов. Функция  называется дифференцируемой в точке называется дифференцируемой в точке  , если в этой точке полное приращение можно представить в виде , если в этой точке полное приращение можно представить в виде  , где , где  Полным дифференциалом функции
Полным дифференциалом функции  называется главная часть полного приращения называется главная часть полного приращения  , линейная относительно приращений аргументов , линейная относительно приращений аргументов  и и  , то есть , то есть  Полный дифференциал функции
Полный дифференциал функции  вычисляется по формуле вычисляется по формуле  Для функции трех переменных
Для функции трех переменных  .
Частными производными второго порядка от функции .
Частными производными второго порядка от функции  называются частные производные от ее частных производных первого порядка. Обозначения частных производных второго порядка: называются частные производные от ее частных производных первого порядка. Обозначения частных производных второго порядка:
 ; ;  ; ;
 ; ;  .
Смешанные производные, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой, если они непрерывны: .
Смешанные производные, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой, если они непрерывны:  .
Дифференциалом второго порядка от функции .
Дифференциалом второго порядка от функции  называется дифференциал от ее полного дифференциала, то есть называется дифференциал от ее полного дифференциала, то есть  . Если . Если  и и  – независимые переменные и функция – независимые переменные и функция  имеет непрерывные производные, то дифференциал второго порядка вычисляется по формуле имеет непрерывные производные, то дифференциал второго порядка вычисляется по формуле  .
Пример 3 .
Пример 3  . Найти . Найти  , ,  , ,  .
Решение. Найдем частные производные: .
Решение. Найдем частные производные:  ; ;  . Дифференцируя повторно, получим . Дифференцируя повторно, получим  ; ;
 ; ;  . .
|
Задание для практической работы по теме «Производные и дифференциалы функции нескольких переменных».
Для функции z=f(x,y) найти  ,
,  ,
,  .
.
Вариант 1. z=x3-3xy2 Вариант 6. z=4x2-7xy3
Вариант 2. z=2x2-5xy3 Вариант 7. z= e-x+2xy
Вариант 3. z=5x4-8xy Вариант 8. z=xy
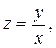 |
Вариант 4. z=6x2-xy3 Вариант 9.
Вариант 5. z=exy Вариант 10. z=x2-2xy3
Практическая работа № 5
Тема 1.5:«Нахождение табличных интегралов. вычисление интегралов с использованием их свойств и таблицы интегралов».
Цель: Находить табличные интегралы, вычислять интегралы с использованием их свойств и таблицы интегралов.
Теоретический материал :
Определение. Функция F(x), дифференцируемая в данном промежутке X, называется первообразной для функции f(x), или интегралом от f(x), если для всякого x Î X справедливо равенство:
F ¢ (x) = f(x).
Нахождение всех первообразных для данной функции называется ее интегрированием. Неопределенным интегралом функции f(x) на данном промежутке Х называется множество всех первообразных функций для функции f(x); обозначение - ò f(x) dx.
Если F(x) - какая-нибудь первообразная для функции f(x), то
ò f(x)dx = F(x) + C,
где С - произвольная постоянная.
Свойства неопределенного интеграла:
1) d ò f(x)=f(x)dx, 2) ò df(x)=f(x)+C,
3) ò af(x)dx=aò f(x)dx (a=const), 4) ò(f(x)+g(x))dx= ò f(x)dx+ ò g(x)dx
Таблица интегралов элементарных функций:


Задание для практической работы по теме «Нахождение табличных интегралов. Вычисление интегралов с использованием их свойств и таблицы интегралов».
Найти неопределенные интегралы используя таблицу интегралов и их свойств:
| Вариант 1 | Вариант 2 |
1. 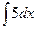 2.
2. 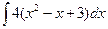 3.
3. 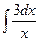 .
4. .
4. 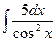 5.
5. 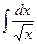
| 1. 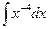 2.
2.  3.
3. 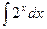 4.
4. 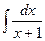 5.
5. 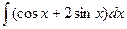
|
| Вариант 3 | Вариант 4 |
1. 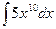 2.
2. 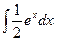 3.
3. 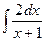 4.
4.  5.
5. 
| 1.  2.
2. 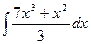 3.
3. 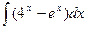 4.
4.  .
5. .
5. 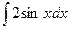
|
| Вариант 5 | Вариант 6 |
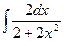
| 
|
Практическая работа № 6
Тема 1.6: «Применение формулы Ньютона-Лейбница, свойства определенного интеграла при вычислениях. Методы интегрирования по частям и подстановкой».
Цель: Применять формулу Ньютона-Лейбница, свойства определенного интеграла при вычислениях. Освоить методы интегрирования по частям и подстановкой.
Теоретический материал :
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 489; Нарушение авторских прав?; Мы поможем в написании вашей работы!