Примеры вычисления

Алгоритм решения.

Примеры вычисления

Алгоритм решения

1. Выписываем характеристическое уравнение для данного уравнения: ak ² + bk + c = 0, находим его дискриминант D = b ² − 4 ac.

2. (а). Если D > 0, общее решение уравнения имеет вид

y = C ₁ e^k ₁ ^x + C ₂ e^k ₂ ^x, где k ₁ = (−b + √D)/ 2 a, k ₂ = (−b−√D)/ 2 a, C ₁, C ₂ — константы.

(б). Если D = 0, общее решение уравнения имеет вид

y =(C ₁ + C ₂ x) e^kx, где k = − b/ 2 a, C ₁, C ₂ — константы.

(в). Если D < 0, общее решение уравнения имеет вид

y = e^αx (C ₁ cos βx + C ₂ sin βx), где α = − b/ 2 a, β = √|D|/ 2 a, C ₁, C ₂ — кон-

станты

3. Если дана задача Коши, подставляем начальные условия в формулу общего решения и находим соответствующее частное решение.

Пример 1. Найти общее решение ДУ: y'' − 5 y' + 4 y = 0.

Характеристическое уравнение k ² − 5 k +4 = 0 имеет дискриминант

D = 25 − 4 ・ 4 = 9 > 0, откуда k ₁ = 4, k ₂ = 1. Общим решением ДУ в этом случае будет y = C ₁ e ^{4 x} + C ₂ e^x, C ₁, C ₂ —константы.

Пример 2. Найти общее решение ДУ: y'' − 10 y' + 25 y = 0.

Характеристическое уравнение k ² − 10 k + 25 = 0 имеет дискриминант

D = 100 − 4 ・ 25 = 0, откуда k = 5. Общим решением ДУ в этом случае будет y = (C ₁ + C ₂ x) e ^{5 x} , C ₁, C ₂ — константы.

Пример 3. Найти общее решение ДУ: y''− 2 y' + 5 y = 0.

Характеристическое уравнение k ² − 2 k +5 = 0 имеет дискриминант

D = 4 − 4 ・ 5 = − 16 < 0, откуда α = 1, β = 2. Общим решением ДУ в этом случае будет y = e^x (C ₁ cos 2 x + C ₂ sin 2 x), C ₁, C ₂ — константы.

Задание для практической работы по теме "Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами"

Найти общее решение дифференциальных уравнений:

Вариант 1. 1). y'' − 2 y' + y = 0,

2).y’’-2y’+3y=0.

Вариант 2. 1). y'' − 5 y' + 6y = 0

2).y’’-4y’+4y=0.

Вариант 3. 1). y ’ ' − 4 y' + 3y= 0

2).y’’+4y’+8y=0.

Вариант 4. 1). y'' +3y' +2 y = 0

2).y’’+6y’+9y=0.

Практическое занятие №10

Тема 1.10:«Нахождение решения дифференциальных уравнений Бернулли».

Цель: Решать дифференциальные уравнения Бернулли.

Теоретический материал :

Дифференциальные уравнения вида

y' + P (x) y = Q (x) y^m (1),

где P (x) и Q (x) — дифференцируемые функции, называют линейным уравнением при m = 0, 1 и уравнением Бернулли при m _ = 0, 1.

1. В уравнении (1) сделаем замену y = uv, dy = udv + vdu,

y' = uv' + vu', где u и v — новые неизвестные функции. В итоге имеем:

uv' + vu' + Puv = Q (uv) ^m

u'v + u (v' + Pv) = Q (uv) ^m

2. Пользуясь произвольностью выбора функции v, положим ее такой, что выражение в первых скобках обнуляется: v_ + P (x) v = 0. Тогда уравнение (1) сводится к системе уравнений:

v' + P (x) v = 0

u'v = Q (x)(uv) ^m (2)

3. Решая систему (2), находим функции u и v; общее решение уравнения (1) записываем в виде y = uv.

4. Если дана задача Коши, подставляем начальные условия в формулу общего решения и находим соответствующее частное решение.

Пример. Найти общее решение уравнения y' + y = −xy ².

Делаем замену y = uv, y' = uv' + vu'. Тогда уравнение примет вид: uv' + vu' + uv = −x (uv)².

Нам нужна не произвольная v, а например одна из таких, для которых v' + v = 0. Тогда уравнение сводится к системе:

v' + v = 0

u'v = −x (uv)²

Из первого уравнения системы имеем:

v' + v = 0

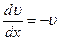
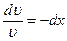
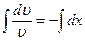
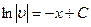
Для конкретной v можно положить C = 0, тогда v = e^−x.

Подставим v во второе уравнение системы:

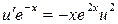
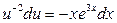
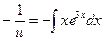
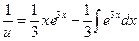
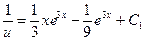
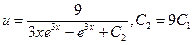
Общее решение:

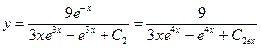
Задание для практической работы по теме «Нахождение решения дифференциальных уравнений»

Найти общее решение дифференциальных уравнений:

Вариант 1 y' + y/x = x ².

Вариант 2. x y' − y = 1/x

Вариант 3. y' -3 y +3 = 0.

Вариант 4. y' + 2y = 4.

Раздел 2. Числовые ряды

Практическая работа № 11

Тема 2.1: «Вычисление членов числового ряда. Вычисление частичных сумм».

Цель: Вычислять члены числового ряда. Вычислять частичные суммы.

Теоретический материал :

Решение задачи, представленной в математических терминах, например, в виде комбинации различных функций, их производных и интегралов, нужно уметь “довести до числа”, которое чаще всего и служит окончательным ответом. Для этого в различных разделах математики выработаны различные методы. Раздел математики, позволяющий решить любую корректно поставленную задачу с достаточной для практического использования точностью, называется теорией рядов. Даже если некоторые тонкие понятия математического анализа появились вне связи с теорией рядов, они немедленно применялись к рядам, которые служили как бы инструментом для испытания значимости этих понятий. Такое положение сохраняется и сейчас.

Выражение вида

,

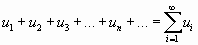где 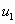; ; 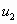;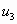…; ;… 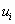- члены ряда; 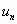- n-ый или общий член ряда, называется бесконечным рядом (рядом).

Если члены ряда:

- числа, то ряд называется числовым;

- числа одного знака, то ряд называется знакопостоянным;

- числа разных знаков, то ряд называется знакопеременным;

- положительные числа, то ряд называется знакоположительным;

- числа, знаки которых строго чередуются, то ряд называется знакочередующимся;

- функции, то ряд называется функциональным;

- степени 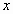, то ряд называется степенным;

- тригонометрические функции, то ряд называется тригонометрическим.

Числовым рядом называется сумма вида

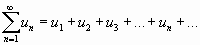, (1)

где 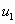, , 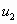,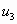…, ,…, 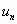называемые членами ряда, образуют бесконечную последовательность; член 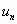называется общим членом ряда.

Суммы

…………..

,

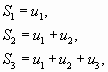
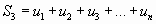составленные из первых членов ряда (1), называются частичными суммами этого ряда. Каждому ряду можно сопоставить последовательность частичных сумм .

Дата добавления: 2014-12-26