Решение. 1. Подставив в общий член ряда вместо n число n+1, получим

1. Подставив в общий член ряда 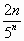вместо n число n+ 1, получим . Найдем предел отношения 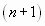-го члена к n- му члену при :

.

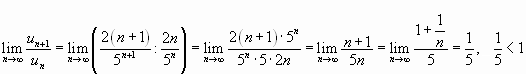Следовательно, данный ряд сходится.

2. Имеем

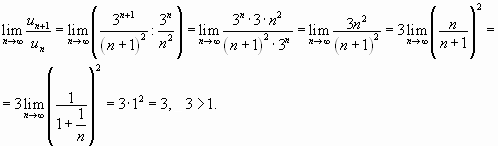
Значит, данный ряд расходится.

3. , т.е. ряд расходится.

Задание для практической работы по теме «Применение необходимого и достаточного признаков сходимости числовых рядов и признака Даламбера»

1. При помощи признака сравнения рядов установить сходимость или расходимость рядов.

2. Исследовать по признаку Даламбера сходимость рядов:

№ вариант	№ задания
Вариант 1.	1. 2.
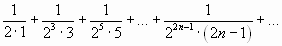
Вариант 2.	1. 2.
Вариант 3.	1. 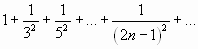2.
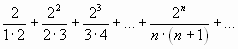
Вариант 4.	1. 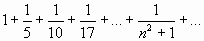2.
Вариант 5.	1. 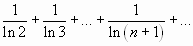2.

Практическая работа № 13

Тема 2.3: «Выделение знакоположительного, знакочередующегося и степенного ряда. Разложение элементарных функций по формуле Тейлора».

Цель: «Выделять знакоположительные, знакочередующиеся и степенные ряды. Разложение элементарных функций по формуле Тейлора».

Теоретический материал :

Числовой ряд

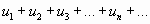
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.

Числовой ряд называется знакочередующимся, если любые два стоящие рядом члена имеют противоположные знаки.

,

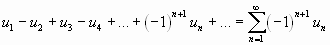где для всех 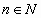(т.е. ряд, положительные и отрицательные члены которого следуют друг за другом поочередно). Например,

;

;

.

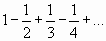Для знакочередующихся рядов имеет место достаточный признак сходимости (установленный в 1714г. Лейбницем в письме к И.Бернулли).

Признак Лейбница. (Абсолютная и условная сходимость ряда). Знакочередующийся ряд сходится, если:

1. последовательность абсолютных величин членов ряда монотонно убывает, т.е. ;

2. общий член ряда стремится к нулю: .

3. при этом сумма S ряда удовлетворяет неравенствам

.

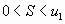Исследование знакочередующегося ряда вида

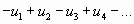
(с отрицательным первым членом) сводится путем умножения всех его членов на 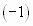к исследованию ряда .

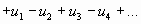Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости.

Теорема. Пусть дан знакопеременный ряд

.

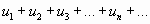Если сходится ряд

,

составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд.

Признак сходимости Лейбница для знакочередующихся рядов служит достаточным признаком сходимости знакочередующихся рядов.

Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов, т.е. всякий абсолютно сходящийся ряд является сходящимся.

Если знакопеременный ряд сходится, а составленный из абсолютных величин его членов ряд расходится, то данный ряд называется условно (неабсолютно) сходящимся.

Дата добавления: 2014-12-26