
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. Пример 1. Записать ряд по его заданному общему члену
|
|
|
|
Примеры вычисления
Пример 1. Записать ряд по его заданному общему члену. Вычислить S4 для заданного числового ряда.
-
 ;
; -
 ;
; -
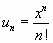 .
.
Решение.
1. Полагая 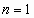 ,
, 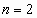 ,
, 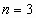 ,…, имеем бесконечную последовательность чисел:
,…, имеем бесконечную последовательность чисел:
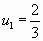 ,
, 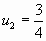 ,
,  . Сложив его члены, получим ряд
. Сложив его члены, получим ряд
 .
.

2.  .
.
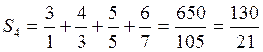
3. Придавая  значения 1,2,3,… и учитывая, что
значения 1,2,3,… и учитывая, что  ,
,  ,
, 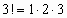 ,…, получим ряд
,…, получим ряд
 .
.
Пример 2. Найти n- ый член ряда по его данным первым членам:
1. 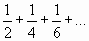 ;
;
2. 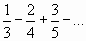 .
.
1. Знаменатели членов ряда, начиная с первого, являются четными числами; следовательно, n- ый член ряда имеет вид  .
.
2. Числители членов ряда образуют натуральный ряд чисел, а соответствующие им знаменатели – натуральный ряд чисел, а соответствующие им знаменатели – натуральный ряд чисел, начиная с 3. Знаки чередуются по закону  или по закону
или по закону 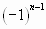 . Значит, n- й член ряда имеет вид
. Значит, n- й член ряда имеет вид 
 или
или 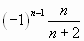 .
.
Задание для практической работы по теме «Вычисление членов числового ряда. Вычисление частичных сумм».
Записать ряд по его заданному общему члену. Вычислить S4 для заданного числового ряда.
Вариант 1. 
Вариант 2. 
Вариант 3. 
Вариант 4. 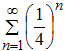
Вариант 5. 
Вариант 6. 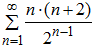
Вариант 7. 
Вариант 8. 
Вариант 9. 
Вариант 10. 
Практическая работа № 12
Тема 2.2: «Применение необходимого и достаточного признаков сходимости числовых рядов и признака Даламбера»
Цель: Применять необходимый и достаточный признак сходимости числовых рядов и признак Даламбера.
Теоретический материал :
Если при бесконечном возрастании номера n частичная сумма ряда  стремится к пределу
стремится к пределу  , то ряд называется сходящимся, а число
, то ряд называется сходящимся, а число  - суммой сходящегося ряда, т.е.
- суммой сходящегося ряда, т.е.
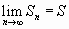 и
и  .
.
Эта запись равносильна записи
 .
.
Если частичная сумма  ряда (1) при неограниченном возрастании n не имеет конечного предела (стремится к
ряда (1) при неограниченном возрастании n не имеет конечного предела (стремится к  или
или 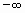 ), то такой ряд называется расходящимся. Если ряд сходящийся, то значение
), то такой ряд называется расходящимся. Если ряд сходящийся, то значение  при достаточно большом n является приближенным выражением суммы ряда S.
при достаточно большом n является приближенным выражением суммы ряда S.
Разность  называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е.
называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е.  , и наоборот, если остаток стремится к нулю, то ряд сходится.
, и наоборот, если остаток стремится к нулю, то ряд сходится.
Пример рядов.
Пример1. Ряд вида
 (2)
(2)
называется геометрическим 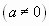 .
.
Геометрический ряд образован из членов геометрической прогрессии.
Известно, что сумма её первых n членов 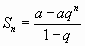 . Очевидно: это n- ая частичная сумма ряда (1.2).
. Очевидно: это n- ая частичная сумма ряда (1.2).
Возможны случаи:
 :
:
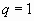 .
.
Ряд (1.2) принимает вид:
 ,
,
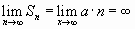 ,ряд расходится;
,ряд расходится;
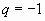
Ряд (1.2) принимает вид:
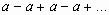 ,
,

 не имеет предела, ряд расходится.
не имеет предела, ряд расходится.
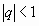 ,
,
 - конечное число, ряд сходится.
- конечное число, ряд сходится.
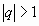 ,
,
 - ряд расходится.
- ряд расходится.
Итак, данный ряд сходится при 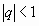 и расходится при
и расходится при 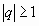 .
.
Пример 2. Ряд вида
 (1.3)
(1.3)
называется гармоническим.
Запишем частичную сумму этого ряда:
 .
.
Сумма  больше суммы, представленной следующим образом:
больше суммы, представленной следующим образом:
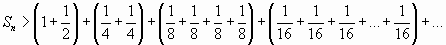
или 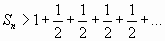 .
.
Если  , то
, то  , или
, или  .
.
Следовательно, если  , то
, то 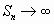 , т.е. гармонический ряд расходится.
, т.е. гармонический ряд расходится.
Пример 3. Ряд вида
 (1.4)
(1.4)
называется обобщенным гармоническим.
Если 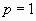 , то данный ряд обращается в гармонический ряд, который является расходящимся.
, то данный ряд обращается в гармонический ряд, который является расходящимся.
Если  , то члены данного ряда больше соответствующих членов гармонического ряда и, значит, он расходится. При
, то члены данного ряда больше соответствующих членов гармонического ряда и, значит, он расходится. При  имеем геометрический ряд, в котором
имеем геометрический ряд, в котором 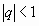 ; он является сходящимся.
; он является сходящимся.
Итак, обобщенный гармонический ряд сходится при  и расходится при
и расходится при 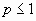 .
.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 6710; Нарушение авторских прав?; Мы поможем в написании вашей работы!