Примеры решения задач по теме №4

Пример 4.1. Начальная фаза гармонического колебания φ=0. Через какое время (в долях периода) скорость точки будет равна половине ее максимальной скорости.

Дано:φ=0,

.

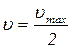Найти: t.

Решение.

Скорость точки, совершающей гармонические колебания определяется законом:

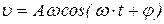, (4.1.1)

где А – амплитуда колебания, 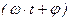– полная фаза колебания, j – начальная фаза, w – собственная круговая частота колебания. Учитывая, что φ=0 и, зная, что , перепишем (4.1.1):

. (4.1.2)

Скорость имеет максимальное значение при , т.е.:

, (4.1.3)

По условию 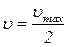, следовательно, с учетом (4.1.2), (4.1.3) имеем:

Следовательно:

.

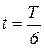Ответ: время, через которое скорость точки будет равна половине ее максимальной скорости .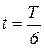

Пример 4.2. Определить период колебаний стержня длиной 60 см около оси, перпендикулярной стержню и проходящей через его конец.

Дано: L=60см=0,6м.

Найти: T.

Решение.

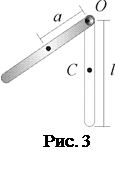
Стержень, имеющий возможность совершать вращение около горизонтальной оси O, не проходящей через центр масс (центр тяжести) C, есть физический маятник (рис. 3). Для физического маятника период колебаний около неподвижной оси:

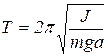, (4.2.1)

где J – момент инерции относительно этой оси, m – масса маятника, a – расстояние от оси колебаний не проходящей через центр масс до центра тяжести (расстояние ОС). Момент инерции относительно оси О, проходящей через конец стержня, можно определить по теореме Штейнера:

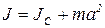, (4.2.2)

где J_c – момент инерции относительно оси, параллельной данной и проходящей через центр тяжести, т.е. относительно оси С. Известно, что для однородного стержня, длиной l:

(4.2.3)

Подставим (4.2.3) в (4.2.2) учитывая, что a=l/2:

. (4.2.4)

Подставив (4.2.4) в (4.2.1), получим:

. (4.2.5)

Убедимся, что правило размерностей выполняется:

.

Подставим в (4.2.5) числовые данные:

.

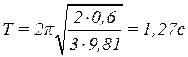Ответ: период колебаний стержня Т=1,27 с.

Дата добавления: 2014-12-26