Механизм выявления спроса в случае непрерывных благ 2 страница

Важным с теоретической точки зрения является понятие чистого общественного блага[19].

Определение. Чистое общественное благо - это благо, обладающее следующими двумя свойствами:

- неисключаемостью, то есть невозможностью исключить из числа его потребителей при конечных издержках ни одно домохозяйство;

- неконкурентностью (несоперничеством), то есть сохранением при потреблении общественного блага одним домохозяйством неизменным количества блага, доступного для потребления другими

Если вместо невозможности исключения при конечных издержках под неисключаемостью понимать необходимость запретительно высоких издержек исключения при данном уровне развития технологии, то некоторые блага будут удовлетворять такому модифицированному определению на данный момент времени. С точки зрения выбора политики в отношении таких благ в рассматриваемый момент определения существенно не различаются. Выше, в начале раздела 3 рассматриваются примеры несовершенной исключаемости.

Наряду с чистыми выделяют смешанные общественные блага, то есть такие, для которых указанные свойства выполняются не в полной мере.

Чистое общественное благо - понятие идеальное, пожалуй, наиболее приближенными к чистому общественному благу примерами служат маяк и национальная оборона.

Однако, как и все идеальные конструкции, понятие чистого общественного блага позволяет выявить свойства таких благ и выдвинуть гипотезы о распределении в экономике с общественными благами.

Неисключаемость приводит к тому, что ценовая система не может обеспечить адекватный контроль объема потребления общественного блага, поскольку если общественное благо произведено, то бюджетное ограничение конкретного индивидуума не может воспрепятствовать выбору им потребления данного блага в пределах всего произведенного объема, а не только той части, в финансировании которой он принял участие. Поэтому нарушаются условия равновесия конкурентной экономики, описанные выше, а также условия теорем общественного благосостояния.

Неконкурентность приводит к тому, что при желании домохозяйства могут потреблять объем общественного блага, равный его совокупному предложению. Вопрос о возможности потреблять меньший объем решается по-разному для разных благ. В экономической теории рассматриваются разные типы общественных благ, для некоторых из них потребление блага может быть уменьшено без издержек, то есть можно свободно избавиться от избыточного количества общественного блага. Мы ограничимся рассмотрением ситуаций, в которых на общественное благо будет распространяться ненасыщаемость, тогда это условие становится излишним.

Могут существовать смешанные общественные блага с перегружаемостью (переполнением). В этом случае, может быть, начиная с определенного числа пользователей, потребление блага дополнительным потребителем приводит к уменьшению выгод от общественного блага, приходящихся на каждого пользователя. Очевидные примеры - парки, пляжи дороги. Перегружаемое общественное благо может быть исключаемым, а может, как в случае с автомобильными дорогами в городе, требовать для исключения запретительно высоких издержек.

Вывод условия эффективного обеспечения общественными благами впервые был предложен Самуэльсоном (1954), и условие эффективного обеспечения обычно называют правилом Самуэльсона.

Мы ограничимся рассмотрением правила для чистых общественных благ без возможности свободного избавления от излишка блага[20]. Чтобы вывод правила было легко сопроводить наглядной графической иллюстрацией, ограничимся случаем, когда число домохозяйств равно двум (отличие вывода для случая произвольного числа домохозяйств незначительно, воспроизведите его самостоятельно), существует единственное доступное общественное благо, объем потребления которого каждым из домохозяйств равен объему его производства и обозначается G. Частное благо единственное (композитное) и объем его потребления домохозяйством h обозначим через x^h, а суммарное потребление частного блага через x.

Предпочтения домохозяйства h описываются функцией полезности:

,

Условие неконкурентности означает, что g для всех одинаково.

Производственное множество описывается выражением

,

где .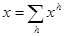

Будем полагать, что предпочтения домохозяйств относятся к «типичным» (well-behaved), а производственное множество выпукло.

Для получения Парето-эффективного размещения, правительство выбирает и G так, чтобы максимизировать уровень полезности первого домохозяйства при ограничениях достижимости размещения и заданности уровня полезности домохозяйства 2 уровнем 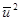. Множество Парето-эффективных размещений представляет собой множество решений данной задачи при различных значениях полезности второго домохозяйства, достигаемых на доступных размещениях.

Функция Лагранжа этой задачи максимизации имеет вид:

,

Условия первого порядка[21]:

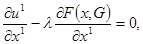
Используя условие

из условий первого порядка получим:

, или

, H =2.

Более общее выражение для n частных благ и произвольного числа H домохозяйств выводится аналогично и имеет вид

,

где - предельная норма замещения частного блага i общественным благом G, а - предельная норма трансформации частного блага i в общественное благо G. [22]

Правило Самуэльсона: Парето-эффективное обеспечение общественным благом достигается тогда, когда предельная норма трансформации каждого из частных благ в общественное равна сумме предельных норм замещения данного частного блага общественным по всем домохозяйствам.

Приведем графическую иллюстрацию этого вывода правила Самуэльсона[23].

На рисунке 3.2.1 в верхней части изображено пространство благ домохозяйства 2 и выбрана некоторая произвольным образом кривая безразличия U ².

При уровне производства общественного блага G потребление второго домохозяйства, обеспечивающее данный уровень полезности, составляет объем x ². Такое соответствие можно построить при любом уровне G. То есть кривую U ² можно интерпретировать как зависимость x ²(G) при заданном уровне полезности второго домохозяйства. На средней части рисунка изображена граница производственных возможностей TT (в данном случае это граница производственного множества при положительных значениях x и G). При каждом уровне G она задает максимально достижимое значение х. Уровень частного блага, который будет в этом случае доступен первому домохозяйству, определяется из выражения x ¹= x - x ²(G), то есть можно построить кривую FF, задающую зависимость потребления частного блага первым домохозяйством от обеспечения общественным благом g при фиксированном уровне полезности второго домохозяйства. Наклон этой кривой при каждом уровне G равен разности наклонов кривой TT и кривой U ², то есть (MRT_Gx - MRS_Gx ¹). Нижний график изображает пространство благ первого домохозяйства, его карту безразличия и кривую FF.

Максимум полезности первого домохозяйства достигается на самой высокой его кривой безразличия, имеющей общие точки с кривой FF, то есть при выполнении условия равенства предельной нормы замещения первого домохозяйства и наклона FF, а значит при условии MRS_Gx ²= MRT_Gx - MRS_Gx ¹. Это и есть условие Самуэльсона для двух домохозяйств.

Для частного блага условие Парето-эффективного размещения (во внутренней точке)

Интерпретация этих условий различается. В случае частных благ количество блага j, которое каждый из индивидуумов готов отдать за добавочную единицу блага i, должно совпадать с тем количеством j, которое готов обменять рынок, и, соответственно, которое экономика может произвести в случае отказа от единицы i. Отличие в случае общественных благ в том, что добавочная единица общественного блага увеличивает полезность всех домохозяйств, так что общественная выгода от этой добавочной единицы определяется суммированием предельных выгод, измеряемых предельными нормами замещения, по всем домохозяйствам. Или можно сказать, что совокупное количество частного блага, от которого все вместе готовы отказаться ради дополнительной единицы общественного есть сумма предельных норм замещения всех потребителей. В эффективной точке она равна предельным издержкам, задаваемым предельной нормой трансформации. Если сумма предельных норм замещения больше, чем предельная норма трансформации, это означает, что за дополнительную единицу общественного блага в совокупности потребители готовы отдать больше частного блага, чем тот объем, от которого требуется отказаться ради производства дополнительной единицы общественного блага. То есть если правительство установит для каждого домохозяйства выраженный в единицах частного блага паушальный налог, чуть меньший, чем MRS этого домохозяйства, причем так, чтобы в сумме эти налоги составили предельную норму трансформации, то в итоге все выиграют.

Обратим внимание на следующее:

При выводе правила Самуэльсона свойство неисключамости общественного блага не было использовано. Парето-эффективный уровень обеспечения общественным благом не зависит от возможности исключения.

Однако неисключаемость может играть существенную роль при анализе функционирования того или иного механизма финансирования общественного блага (того, каким образом будет определяться вклад каждого домохозяйства в обеспечение общественного блага). Предположим, что каждому предложено добровольно определить свой вклад. Например, речь идет о ситуации, описанной выше, когда сумма предельных норм замещения выше, чем предельная норма трансформации и речь идет об отказе от некоторого количества частного блага в обмен на единицу общественного. Увеличение вклада только одного потребителя приведет к его личному выигрышу в полезности, если его собственная предельная норма замещения выше, чем предельная норма трансформации и поэтому, если у каждого из нескольких потребителей при заданном уровне производства общественного блага предельные нормы замещения меньше предельной нормы трансформации, то даже если в сумме они предельную норму трансформации превышают, ни один из них не найдет для себя выгодным пожертвовать своим потреблением частного блага ради добавочной единицы общественного.

Следует также понимать, что правило Самуэльсона, при всей его простоте, сложно применить на практике. При выводе правила Самуэльсона предполагалось, что правительство имеет полный контроль над размещением ресурсов. Одно из очевидных на первый взгляд решений - использовать паушальное налогообложение для перераспределения дохода и для финансирования обеспечения общественного блага с децентрализацией обеспечения частными благами. Однако оптимальный паушальный налог редко может быть применен на практике, и по этой же причине трудно его применить для практической реализации правила Самуэльсона.

Рассмотрим, какое равновесие может сложиться в случае частного производства общественного блага при добровольн ом участии в его финансировании.

Несколько упростим модель, чтобы результат получил наглядную графическую интерпретацию[24].

По-прежнему рассматриваем только двух агентов. Обозначим g ¹, g ², w ¹, w ² соответственно вклады домохозяйств в обеспечение общественным благом, и их первоначальные наделенности частным благом x. Объем общественного блага равен f (g ₁+ g ₂), полезность агента i описывается функцией Uⁱ (f (g ¹+ g ²), wⁱ - gⁱ). Можно как включать производственную функцию в функцию полезности, так и просто записать uⁱ (g ¹+ g ², wⁱ - gⁱ), где uⁱ (G, xⁱ) = Uⁱ (f (G), xⁱ). Включение технологии в функцию полезности не приводит к потере общности, так как, в конечном счете, полезность зависит от общего вклада в общественное благо.

Предположим, что каждое домохозяйство независимо решает, сколько ему пожертвовать на производство общественного блага. Если агент 1 думает, что вклад агента 2 будет, например, g ², то задача максимизации агента 1 примет вид:[Неизвестн2]

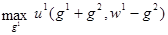
при ограничении g ¹³0.

Ограничение g ¹³0 является естественным ограничением в данном случае; оно говорит о том, что агент 1 может добровольно увеличить объем общественного блага, но он не может в одностороннем порядке уменьшить его.

Это ограничение является важным.

Условие первого порядка Куна-Таккера для этой задачи:

,

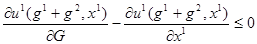причем равенство выполняется, когда g ¹>0.

Мы можем также переписать это условие как

MRS _Gx ¹£1.

Если агент жертвует положительную величину, предельная норма замещения частного блага общественным должна быть равна предельным издержкам общественного блага (в данном случае 1). Если его предельная норма меньше предельных издержек, он не захочет вносить свой вклад в производство общественного блага.

Условие иллюстрирует рисунок 3.2.1. «Наделенность» агента 1 представлена точкой (w ¹, g ²), так как объем частного потребления при нулевом пожертвовании равен w ¹, а объем потребления общественного блага – g ². Бюджетная линия проходит через эту точку с наклоном 1. Доступные точки на бюджетной линии удовлетворяют условию

g ¹= w ¹- x ¹³0.

На рисунке представлено два случая: в первом агент желает внести положительный вклад, во втором предпочитает быть «безбилетником».

Равновесие Нэша в этой игре – множество вкладов (g ¹*, g ²*), такое, что каждый агент жертвует свой оптимальный объем при заданном вкладе другого агента. То есть условие MRS _Gx ¹£1 должно удовлетворяться для обоих агентов.

Условия, характеризующие равновесие Нэша можно записать следующим образом:

.

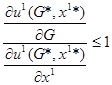
Если производится положительный объем G, то по крайней мере одно из этих неравенств должно выполняться как равенство. Если предельная норма замещения другого агента в этом случае не равна нулю, то условие Самуэльсона нарушается, сумма предельных норм замещения получается большей единицы. Посмотрим, как на правой части рисунка 3.2.1 отражено положение агента, не делающего вклада в обеспечение общественным благом. Его предельная норма замещения частного блага общественным меньше единицы. То есть он согласился бы обменять одну единицу общественного блага на меньше, чем единицу, частного. Но его связывает ограничение положительности вклада. Он выберет нулевой вклад и будет пользоваться благом бесплатно. В этом и заключается существо «проблемы безбилетника».

Это происходит в силу невозможности исключения его из пользования общественным благом. Если бы исключение было возможным, то при наличии неконкурентности тот, кто заплатил за благо, получил бы право контроля над ним и мог бы, например, потребовать от второго компенсации за доступ к выгодам от блага. Эта компенсация могла бы быть меньше единицы за каждую единицу блага. В итоге бюджетное ограничение, изображенное в левой части рисунка 3.2.1 сместилось бы в направлении от начала координат и изменило наклон, так что объем производства неконкурентного блага возрос бы. У индивидуума, чье положение изображено на правом рисунке бюджетное ограничение сдвинулось бы в результате тоже вправо, и тоже изменило бы наклон. То есть для каждого из них цена единицы общественного блага была меньшей, чем издержки производства этой единицы, каждый был бы готов внести свой положительный вклад, суммарный объем производства общественного блага возрос бы. Условие максимизации полезности одного индивидуума при его предположениях о вкладе другого позволяет построить функцию реакции. Пересечение функций реакции задаст равновесие Нэша в данной задаче.

Естественным является вопрос, возможна ли какая-нибудь форма экономики, в которой конкурентное поведение в присутствии общественных благ приводило бы к Парето-эффективному исходу[25]? В модели общего равновесия с равными для всех покупателей ценами за единицу блага он не достигается, хотя бы потому, что потребители имеют различную оценку потребляемого объема, а значит и предложения общественного блага. Условие уплаты всеми равной цены за указанный объем, следовательно, не является эффективным. Тот, для кого цена завышена, предпочел бы отказаться от единицы общественного блага в обмен на потребление других благ, а тот, у кого цена занижена, готов отказаться от некоторого количества частного блага в пользу увеличения производства общественного. Одна из основных проблем в том, что первый не может реализовать свое желание: его нельзя исключить из потребления произведенного блага.

Отсюда следует гипотеза, что Парето-эффективности можно было бы достичь, если бы каждый потребитель платил индивидуальную или персонифицированную цену за благо, причем эта цена отражала бы его субъективную оценку блага. Допущение о возможности таких персонифицированных цен создает модель, являющуюся расширением экономики Эрроу-Дебре, предполагающей единственность цены каждого товара.

Концепция равновесия с персонифицированными ценами была предложено Линдалем в 1919 году, и его часто называют равновесием Линдаля. Персонифицированные цены, складывающиеся при таком равновесии, называются ценами Линдаля.

Позднее модель была развита и возможны различные варианты построения равновесия Линдаля. Первый формальный анализ равновесия Линдаля выполнен Йохансеном в 1963 году (Johansen, “Some Notes on the Lindahl Theory of the Determination of Public Expenditures”, International Economic Review, 4,3).

Рассмотрим один из вариантов равновесия Линдаля, для простой экономики с двумя домохозяйствами, в которой цена общественного блага для потребителя задана как доля издержек на общественное блага, которую каждое домохозяйство должно покрыть. Покажем, как в конкурентной экономике с корректно определенными персонифицированными ценами может поддерживаться эффективность. 4.1 Простая модель

Каждое домохозяйство основывает свое решение о потреблении на доле t^h в издержках обеспечения общественным благом, которую оно должно уплатить. При предположении, что спрос домохозяйства h (h= 1,…, H) на общественное благо неограниченно возрастает при t^h®0, равновесие может быть определено как множество долей в издержках, {t1,…,tH}, в сумме равных 1 и приводящим к одинаковому объему спроса на общественное благо у всех домохозяйств. Важность такого равновесия в том, что оно удовлетворяет правилу Самуэльсона и, следовательно, Парето-эффективно несмотря на существование общественного блага. Если общественных благ много, доли в издержках должны определяться для каждого общественного блага, и эффективность будет также достигнута.

Рассмотрим экономику с двумя домохозяйствами h =1,2,, имеющими наделенность w^h единицами некоторого товара, служащего масштабом цен, который они предлагают неэластичным образом на рынок (например, это может быть труд, в том случае, когда решение об объеме предложения труда принимается экзогенно). Каждое домохозяйство, следовательно, имеет фиксированный доход в размере w^h. Существует единственное частное благо, производимое с постоянной отдачей от масштаба с использованием только товара, служащего масштабом цен и единица измерения этого блага выбрана так, что единица выпуска требует одной единицы фактора, то есть товара, служащего масштабом цен. Цена частного блага, следовательно, также равна 1. Производство общественного блага осуществляется с постоянной отдачей от масштаба, и каждая единица требует p_G единиц труда. Предельная норма трансформации в производстве между общественным и частным благами, следовательно, постоянна и равна p_G.

Пусть каждое домохозяйство имеет функцию полезности вида:

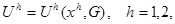
где x^h - количество потребляемого единственного (точнее, композитного) частного блага, а G - количество потребляемого и предлагаемого общественного блага. Полезность не убывает по x^h и G. Обозначим G^h количество общественного блага, которое домохозяйство желало бы потребить, если его бюджетное ограничение имеет вид:

,

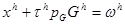где p_GG^h -совокупные издержки производства блага и t^h - доля издержек, уплачиваемая h.

Отсюда следует, что домохозяйство h выбирает G^h, максимизируя

Условие максимума первого порядка:

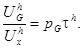
Решая последнее уравнение относительно G^h, получим функцию реакции Линдаля:

которая описывает спрос домохозяйства на общественное благо как функцию от его доли в издержках и первоначальной наделенности. Если функция полезности строго вогнута и условия второго порядка для задачи максимизации удовлетворены, то L^h (·) - убывающая функция по t^h.

Равновесием Линдаля называется пара долей в издержках такая, что

(i) и

(ii)

Первое из условий гарантирует, что будет получено достаточно доходов для финансирования равновесного обеспечения общественным благом, а второе, что домохозяйства будут оба удовлетворены предложением. Из того, что полезность не убывает по G, следует, что доли в издержках неотрицательны.

Природа равновесия Линдаля иллюстрируется на рисунке 3.2.1. Функции реакции Линдаля строятся как геометрические места точек касания вертикалей кривыми безразличия (линиями уровня функций полезности), а равновесие задается пересечением функций реакции. В точке равновесия кривые безразличия двух домохозяйств касаются. Докажем выполнение в равновесии равенства суммы предельных норм замещения MRS_Gx^h предельной норме трансформации MRT_Gx. Необходимое условие первого порядка в равновесии выполняется для обоих домохозяйств. Суммируя значения предельных норм замещения, полученные из условия первого порядка для каждого домохозяйства, получим:

Последнее выражение представляет собой правило Самуэльсона для экономики с общественными благами, отсюда следует, что равновесие Линдаля Парето-эффективно. Это утверждение представляет собой формулировку Первой теоремы общественного благосостояния для равновесия Линдаля (здесь в упрощенной версии). Чтобы корректно сформулировать Вторую теорему общественного благосостояния потребуется некоторое изменение модели, вводящее перераспределение наделенности. С формальными утверждениями этих теорем и их доказательствами можно ознакомиться в [3]. Для нас важно, что путем перераспределения первоначальной наделенности можно получить новое равновесие Линдаля, которое представляет другую точку во множестве Парето-эффективных исходов.

К сожалению, если принять во внимание возможность стратегического взаимодействия экономических агентов в данной модели, равновесие Линдаля и, следовательно, эффективный уровень обеспечения общественным благом может не достигаться.[26] Допустим, что первое домохозяйство знает функцию реакции второго домохозяйства (то есть его стратегию) и предполагает, что второе домохозяйство будет ее придерживаться. Тогда ему выгодно добиться результата, при котором его полезность будет максимальной. Кривая безразличия Ue ¹ не является наилучшей из имеющих общие точки с кривой реакции второй фирмы. Такая кривая безразличия - это U ¹₀. Значит ему выгодно заявить такую «функцию реакции», которая приведет не к равновесию в точке t*, а к равновесию t⁰. То есть стратегия объявления своей истинной кривой реакции на доли вклада в обеспечение общественным благом не является наилучшим ответом (best response) на стратегию объявления правды другими участниками, то есть при стратегическом взаимодействии набор стратегий (L ¹, L ²) не является равновесием по Нэшу.

Нетрудно видеть, что в рассмотренных случаях возможность установления адекватной платы за общественное благо связана с проблемой выявления истинного спроса экономического агента на общественное благо. Один из способов, позволяющих выявить спрос и установить эффективный объем производства общественного блага задается механизмом Гровса-Кларка[27].

Рассмотрим сначала случай с дискретным общественным благом, которое или производится или не производится (модель можно распространить на ситуацию, когда принимается решение увеличивать или не увеличивать объем производства общественного блага). Пусть G может быть 0 или 1. Потребляются два блага - общественное и частное (композитное). Функция полезности квазилинейна. Пусть r_i – цена резервирования агента i и s_i –доля издержек агента i в обеспечении общественным благом[28]. Если издержки обеспечения общественным благом равны c, то s_ic – общая сумма денег, которую должен уплатить агент i. Обозначим v_i=r_i – s_ic чистую ценность общественного блага для агента i. Производство общественного блага приведет к улучшению с точки зрения компенсационного критерия, если 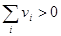. Эффективный объем производства общественного блага требует выполнения условия .

Один из механизмов, которые можно использовать, – просто спрашивать каждого агента о его чистой ценности общественного блага и производить благо в том случае, если сумма этих заявленных ценностей неотрицательна. Проблема в том, что эта схема не обеспечивает достаточных стимулов для индивидуальных агентов выявлять свою истинную готовность платить. Например, если чистая ценность агента 1 выше нуля при любом объеме, он может заявить произвольно большую сумму. Пока заявка не влияет на то, сколько он платит, но влияет на то, будет или не будет произведено общественное благо, он может заявлять стоимость настолько большую, насколько возможно.

Механизм Гровса-Кларка

Дата добавления: 2014-12-26