Тема 1. Модели детерминированных сигналов

Использованная при разработке учебного пособия

1. Андреев В.И. Педагогика. Учебный курс для творческого саморазвития. – Казань, 2000

2. Афонина Г.М. Педагогика. Курс лекций и семинарские занятия. – Ростов - н/Д, 2002

3. Морева Н.А. Педагогика среднего специального образования /Отв. ред. С.И. Самыгин. – Ростов - н/Д, 1998

4. Сластенин В.В., Каширин В.П. Психология и педагогика. – М., 2001

5. Смирнов С.Д. Педагогика и психология высшего образования. От деятельности к личности. – М., 2001

Задача 1.1.

Найти спектр последовательности косинусоидальных импульсов (рис. 1).

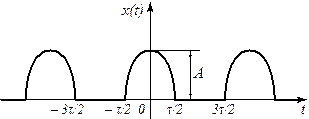
Рис. 1.

Задача 1.2.

Определить спектр амплитуд периодической последовательности прямоугольных импульсов длительностью 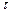и амплитудой , следующих с частотой (рис. 3), описываемых как:

Рис. 3.

Задача 1.3.

Найти спектральную характеристику одиночного прямоугольного импульса:

По найденной построить линейчатый спектр периодической последовательности этих импульсов.

Задача 1.4.

Найти спектр дельта-функции, отличной от нуля в начале координат:

.

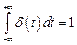Задача 1.5.

Найти спектр одиночного импульса высокочастотных колебаний (рисунок 5).

Рис. 5.

Задача 1.6.

Найти спектр одиночного экспоненциального импульса.

Задача 1.7.

Найти спектр сигнала включения:

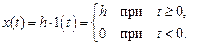
Задача 1.8.

Пусть в задаче 1.2 длительность прямоугольного импульса увеличилась в 2 раза:

Как изменится при этом спектральная характеристика?

Задача 1.9.

Для периодической последовательности импульсов (задача 1.4) вычислить первые пять членов рядя Фурье. Оценить энергетический вклад (в %) постоянной составляющей и первой гармоники при .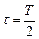

Задача 1.10.

Определить практическую ширину спектра периодической последовательности прямоугольных импульсов при ширине импульсов 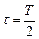для случая, когда должны быть учтены все гармонические составляющие сигнала, содержащие не менее 95% общей мощности сигнала.

Указание.

При решении задачи воспользоваться результатами, полученными при решении задач 1.4, 1.9.

Дата добавления: 2014-12-26