Связь между различными типами задачи ЛП

Покажем, что общая задача ЛП может быть сведена как к однородной задаче ЛП, так и к канонической.

I. Вначале сведём общую задачу к однородной. В соответствии с определением 1 п.1.3 для этого достаточно каждое ограничение вида равенства:

,

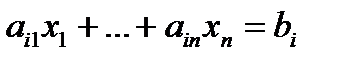заменить на равносильную систему неравенств:

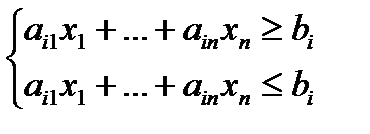
Все ограничения задачи будут иметь вид неравенства и задача станет однородной. При этом число ограничений, конечно же, увеличится.

II. Теперь сведем общую задачу ЛП к канонической. Для этого следует, во-первых, представить каждое неравенство в виде равенства и, во-вторых, добиться того, чтобы все переменные задачи были неотрицательны. Для каждого неравенства системы ограничений вида «меньше»

,

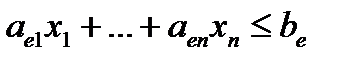добавим новую (балансовую) переменную 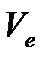, определяемую равенством:

.

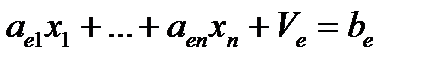Для каждого неравенства системы ограничений вида «больше»

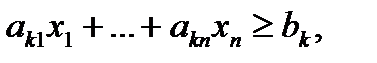
введем переменную 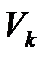, определяемую равенством:

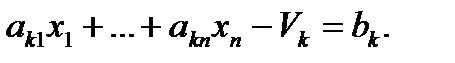
Ясно, что так определенные балансовые переменные 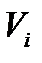неотрицательны. Таким способом все неравенства могут быть заменены на равенства.

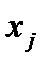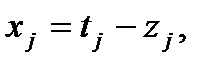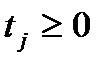Для каждой переменной , на которую не наложено тривиальное ограничение, положим: где и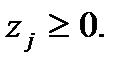

Заменив все такие 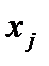на 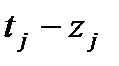, получим эквивалентную задачу, в которой все переменные неотрицательны. Поскольку ранее мы уже добились того, что все ограничения задачи имеют вид равенства, то полученная задача оказывается канонической.

Пример 1. Пусть дана задача ЛП

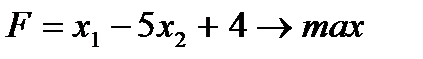
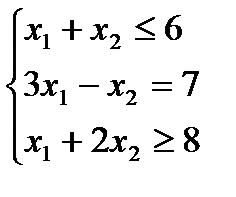(1)

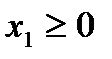
Требуется преобразовать исходную общую задачу ЛП к другим формам задачи ЛП.

1. Сведем эту задачу к однородной форме.

Заменяя равенство из (1) на систему неравенств получим соответствующую однородную задачу:

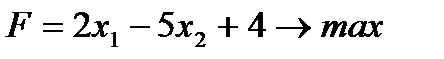
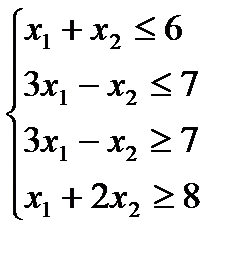(2)

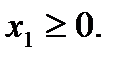
2. Сведем задачу к каноничной форме. Добавим неотрицательные балансовые переменные 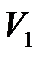и 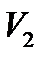, превращая первое и третье ограничения в равенства:

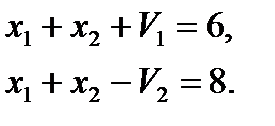
Заменим переменную :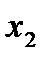

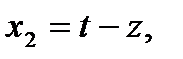
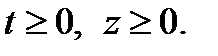
Тогда получим каноническую задачу:

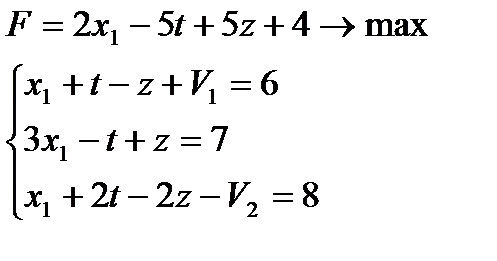(3)

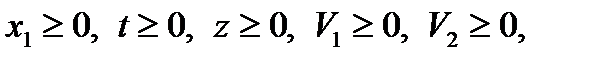
фактически равносильную исходной.

Таким образом, показано, что общая, однородная и канонические формы задачи ЛП могут быть сведены друг к другу.

Сведение произвольной канонической задачи ЛП к симплексной форме будет рассмотрено в следующих параграфах.

Укажем на один частный случай сведения однородной задачи ЛП к симплексной форме. Пусть дана задача о ресурсах, то есть однородная задача ЛП вида:

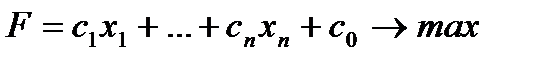
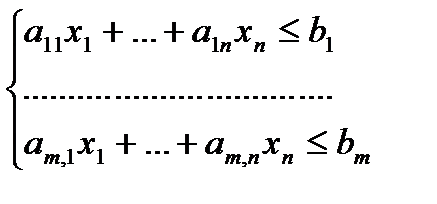(4)

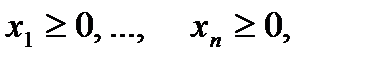
причем все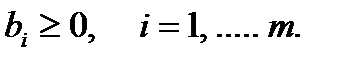

Сведем эту задачу к канонической с помощью введения балансовых переменных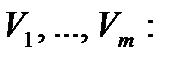

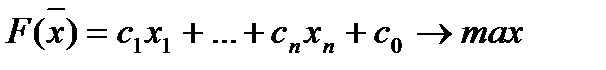
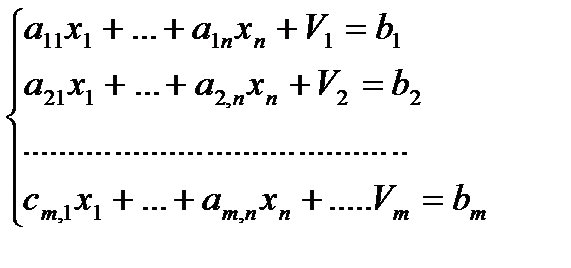(5)

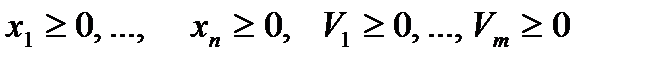
Полученная каноническая задача ЛП на самом деле является симплексной, поскольку, во-первых, столбец свободных членов 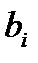состоит только из неотрицательных элементов, во-вторых, система уравнений имеет разрешенный вид (столбцы переменных 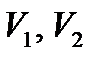, …, 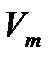и сами переменные являются базисными), в-третьих, целевая функция F зависит только от свободных переменных .

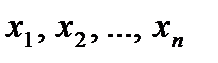Дата добавления: 2014-12-26