
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример решения задачи линейного программирования симплекс-методом
|
|
|
|
Симплекс-метод решения задачи линейного программирования.
Рассмотрим однородную задачу ЛП из примера №1 п. 1.5.:
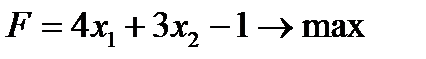
 (1)
(1)

Добавив к левым частям системы неравенств соответствующие балансовые переменные 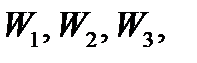 преобразуем задачу (1) в каноническую форму:
преобразуем задачу (1) в каноническую форму:
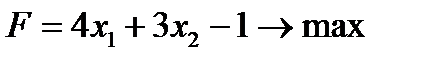
 (2)
(2)
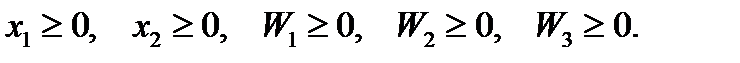
Для удобства и единообразия запишем определение целевой функции 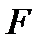 в виде уравнения:
в виде уравнения:
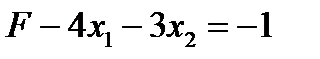 (3)
(3)
Запишем (2) и (3) в виде первой симплекс таблицы:

| 
| 
| 
| 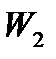
| 
| 
| |
| - 2 | (4) | ||||||
| - 1 | |||||||
| - 4 | - 3 | - 1 |
Первые три строки таблицы (4) содержат по сути расширенную матрицу системы линейных уравнений (2), к которой слева приписан столбец переменной 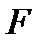 . Последняя строка, называемая индексной, содержит уравнение (3). Буквой
. Последняя строка, называемая индексной, содержит уравнение (3). Буквой  , как обычно, обозначен столбец свободных членов. Отметим, что таким образом составленная таблица (4) называется симплексной, поскольку задача (2) имеет симплексную форму. Напомним, что это означает, что во-первых, матрица системы (и таблица (4)) содержат т базисных столбцов (столбцы
, как обычно, обозначен столбец свободных членов. Отметим, что таким образом составленная таблица (4) называется симплексной, поскольку задача (2) имеет симплексную форму. Напомним, что это означает, что во-первых, матрица системы (и таблица (4)) содержат т базисных столбцов (столбцы  ), где т - число уравнений (в данном случае
), где т - число уравнений (в данном случае  ); во-вторых, все элементы столбца свободных членов неотрицательны (это числа 8, 9 и 10), кроме, возможно, элемента индексной строки; в- третьих, целевая функция
); во-вторых, все элементы столбца свободных членов неотрицательны (это числа 8, 9 и 10), кроме, возможно, элемента индексной строки; в- третьих, целевая функция  зависит только от свободных переменных (
зависит только от свободных переменных ( и
и  ). Последнее верно, поскольку в базисных столбцах (
). Последнее верно, поскольку в базисных столбцах ( ) в индексной строке находятся только нули. Первая симплекс-таблица (4) определяет первое опорное решение. Напомним, что опорное решение является допустимым базисным решением, и, следовательно, свободные переменные
) в индексной строке находятся только нули. Первая симплекс-таблица (4) определяет первое опорное решение. Напомним, что опорное решение является допустимым базисным решением, и, следовательно, свободные переменные 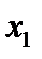 и
и  равны нулю:
равны нулю: 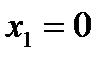 и
и  .
.
Далее, переменная 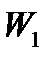 определяется первой строкой таблицы (4), которая является сокращённой записью первого уравнения системы (2). При
определяется первой строкой таблицы (4), которая является сокращённой записью первого уравнения системы (2). При 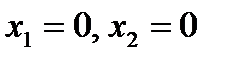 оно принимает вид:
оно принимает вид:

Вторая строка таблицы определяет переменную 

Третья строка определяет 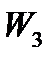 :
: 

Значение целевой функции определяем по индексной строке: 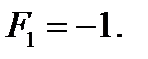
В дальнейшем мы покажем, что оптимальное решение канонической задачи ЛП является опорным, и, следовательно, его следует искать среди опорных решений. Симплекс-таблица (4) и дает одно из таких решений. Как проверить, является ли оно оптимальным? Оказывается, просто. Как мы увидим далее, если коэффициенты  целевой функции
целевой функции 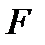 канонической задачи ЛП неположительные:
канонической задачи ЛП неположительные:  ,- и функция
,- и функция 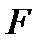 зависит только от свободных переменных, то соответствующее опорное решение является оптимальным.
зависит только от свободных переменных, то соответствующее опорное решение является оптимальным.
Но условие  означает, что коэффициенты индексной строки, стоящие в столбцах свободных переменных, должны быть неотрицательны:
означает, что коэффициенты индексной строки, стоящие в столбцах свободных переменных, должны быть неотрицательны: 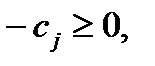 поскольку индексная строка соответствует уравнению:
поскольку индексная строка соответствует уравнению:  , - и содержит коэффициенты
, - и содержит коэффициенты  с противоположным знаком.
с противоположным знаком.
Мы видим, что в таблице (4) условие неотрицательности всех элементов индексной строки (разумеется, кроме правой части 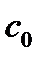 , стоящей в столбце свободных членов) не выполнено. Более того, оба столбца свободных переменных
, стоящей в столбце свободных членов) не выполнено. Более того, оба столбца свободных переменных 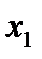 и
и  содержат в индексной строке отрицательные элементы: - 4 и -3, - соответственно.
содержат в индексной строке отрицательные элементы: - 4 и -3, - соответственно.
Выберем любой из этих столбцов, например, первый и назовем его ведущим. Определим для каждого  так называемое допустимое отношение
так называемое допустимое отношение 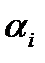 следующим образом. Если в
следующим образом. Если в 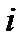 - ой строке ведущего столбца стоит неположительный элемент, то положим
- ой строке ведущего столбца стоит неположительный элемент, то положим 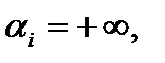 если же этот элемент
если же этот элемент  то положим
то положим
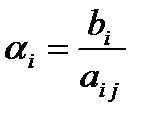 ,
,
где 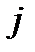 - номер ведущего столбца.
- номер ведущего столбца.
В нашем случае  и допустимые отношения
и допустимые отношения  соответственно равны:
соответственно равны:

Добавим к симплекс-таблице (4) столбец 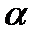 :
:
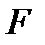
| 
| 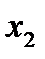
| 
| 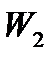
| 
| 
| 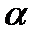
| |
| - 2 | 
| (5) | ||||||
| - 1 | ||||||||
| - 4 | - 3 | - 1 |
В таблице (5) отрицательный элемент – 4 ведущего столбца взят в рамочку, для того чтобы выделить ведущий столбец. Можно, разумеется, выделить этот столбец и любым другим разумным образом: цветом, шрифтом и т.п.
Среди всех допустимых отношений 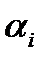 найдем наименьшее:
найдем наименьшее: 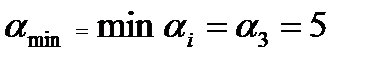 .
.
Наименьшее допустимое отношение соответствует третьей строке таблицы, которую мы теперь объявляем ведущей строкой. На пересечении ведущей строки и ведущего столбца стоит ключевой элемент таблицы. В нашем случае это 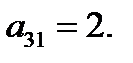 Выделим в таблице (5) минимальное допустимое отношение и ключевой элемент, рамочкой:
Выделим в таблице (5) минимальное допустимое отношение и ключевой элемент, рамочкой:
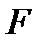
| 
| 
| 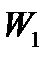
| 
| 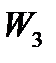
| 
| 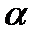
| |
| - 2 | 
| (6) | ||||||
| - 1 | 5 = 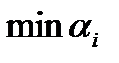
| |||||||
| - 4 | - 3 | - 1 |
Дальнейшая наша цель состоит в том, чтобы преобразовать методом Гаусса таблицу (6) в новую симплекс-таблицу, первый столбец который стал бы базисным, содержащим число 1 в ведущей (третьей) строке.
Вначале разделим ведущую строку на ключевой элемент:
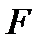
| 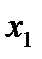
| 
| 
| 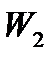
| 
| 
| 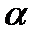
| ||
| - 2 | (7) | ||||||||
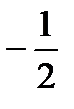
| 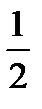
| ||||||||
| - 4 | - 3 | - 1 | |||||||
В таблице (7) мы не заполняем столбец 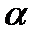 , поскольку он нужен, только для того, чтобы определить ведущую строку, что мы уже сделали. Мы выделили только ключевой элемент, так как он определяет одновременно и ведущую строку (третью) и ведущий столбец (первый).
, поскольку он нужен, только для того, чтобы определить ведущую строку, что мы уже сделали. Мы выделили только ключевой элемент, так как он определяет одновременно и ведущую строку (третью) и ведущий столбец (первый).
Проделаем теперь следующие преобразования Гаусса:
1) вычтем из первой строки ведущую (третью) строку;
2) прибавим ко второй строке ведущую, умноженную на 2;
3) прибавим к индексной строке ведущую, умноженную на 4.
В итоге получим новую таблицу:
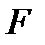
| 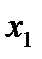
| 
| 
| 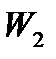
| 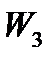
| 
| 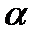
| ||

| 
| ||||||||
| (8) | |||||||||

| 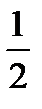
| ||||||||
| - 5 | |||||||||
Нетрудно видеть, что мы получили симплекс-таблицу. Действительно, в таблице (8) после перестановки столбца 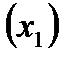 со столбцом
со столбцом 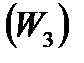 в последних трех столбцах получается единичная матрица; столбец свободных членов неотрицателен; целевая функция
в последних трех столбцах получается единичная матрица; столбец свободных членов неотрицателен; целевая функция  зависит только от свободных переменных
зависит только от свободных переменных 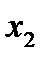 и
и 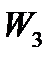
Отметим, что столбец 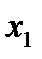 , став базисным, вытеснил «из базиса» столбец
, став базисным, вытеснил «из базиса» столбец 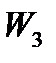 . В силу этого обстоятельства проделанный процесс называют операцией однократного замещения. В данном случае эта операция состояла из последовательности элементарных преобразований Гаусса 1), 2) и 3).
. В силу этого обстоятельства проделанный процесс называют операцией однократного замещения. В данном случае эта операция состояла из последовательности элементарных преобразований Гаусса 1), 2) и 3).
Таким образом, получена вторая симплекс-таблица (8), которой соответствует второе опорное решение. Переменные  и
и 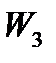 - свободные и, следовательно,
- свободные и, следовательно,  и
и  . Поскольку первое уравнение имеет вид.
. Поскольку первое уравнение имеет вид.

то значение базисной переменной  равно 3:
равно 3: 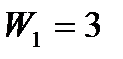 . Базисная переменная
. Базисная переменная  определяется вторым уравнением:
определяется вторым уравнением:

а базисная переменная 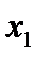 определяется третьим уравнением (так как в столбце
определяется третьим уравнением (так как в столбце 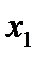 единица стоит в третьей строке):
единица стоит в третьей строке):
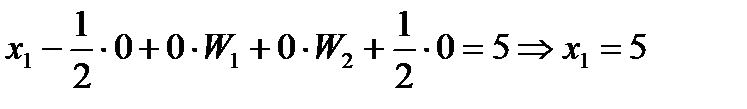
Итак, 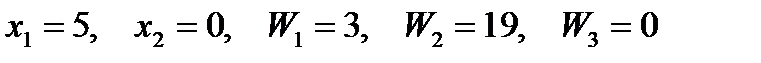 , - второе опорное решение. Новое значение целевой функции
, - второе опорное решение. Новое значение целевой функции  определяется индексной строкой:
определяется индексной строкой: 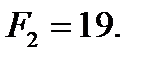
Это опорное решение также не является оптимальным, что следует из того, что в индексной строке таблицы (8) имеется отрицательный элемент (-5) во втором столбце, который мы выберем теперь в качестве ведущего столбца. Затем найдем ведущую строку с минимальным допустимым отношением и ключевой элемент:

| 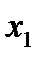
| 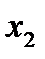
| 
| 
| 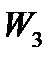
| 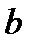
| 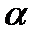
| |

| 
| 2 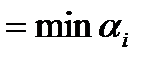
| ||||||
| 9,5 | (9) | |||||||

| 
| 
| ||||||
| - 5 |
Разделим ведущую строку (первую) на ключевой элемент  :
:
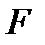
| 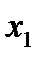
| 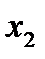
| 
| 
| 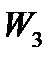
| 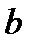
| ||
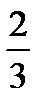
| 
| |||||||
| (10) | ||||||||
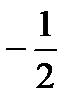
| 
| |||||||
| - 5 | ||||||||
Выполним теперь следующие преобразования Гаусса:
1) вычтем из второй строки первую, умноженную на 2;
2) прибавим к третьей строке первую, умноженную на  ;
;
3) прибавим к индексной строке первую, умноженную на 5. В результате получим третью симплекс-таблицу:

| 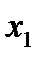
| 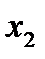
| 
| 
| 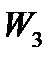
| 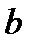
| ||
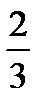
| 
| |||||||

| 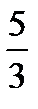
| (11) | ||||||

| 
| |||||||
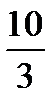
| 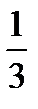
| |||||||
Ей соответствует третье опорное решение:

- и значение целевой функции  .
.
Поскольку индексная строка таблицы (11) не содержит отрицательных элементов, полученное опорное решение будет оптимальным: 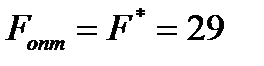 и
и 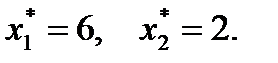 (12) При этом
(12) При этом  Здесь мы звездочками помечаем оптимальные значения переменных.
Здесь мы звездочками помечаем оптимальные значения переменных.
Таким образом, задача (2) и с ней задача (1) решены.
1.8.2. Алгоритм симплекс-метода.
Изложим теперь этот метод решения, в общем виде.
Пусть дана симплексная форма задачи ЛП, то есть каноническая задача ЛП, матрица системы которой имеет разрешенный вид, свободные члены неотрицательны и целевая функция зависит только от свободных переменных:
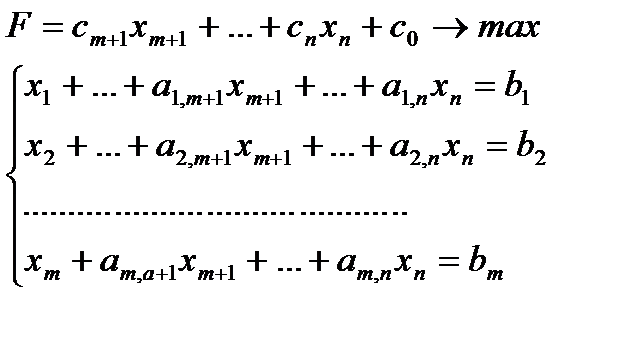 (1)
(1)
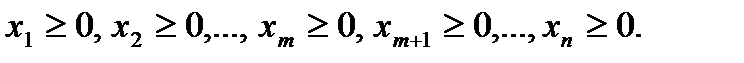
Здесь мы считаем свободными переменные  . Запишем функцию
. Запишем функцию 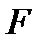 в виде уравнения:
в виде уравнения:
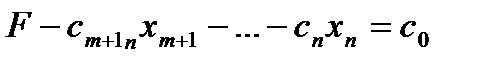 , (2)
, (2)
Уравнениям (1) и (2) соответствует первая симплекс-таблица:
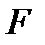
| 
| 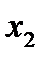
| ….. | 
| 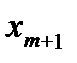
| ….. | 
| 
| |
| ….. | 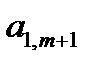
| ….. | 
| 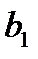
| |||||
| ….. | 
| ….. | 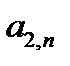
| 
| (3) | ||||
| ….. | ….. | ….. | ….. | ….. | ….. | ….. | ….. | ….. | |
| ….. | 
| ….. | 
| 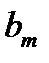 
| |||||
| ….. | 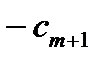
| ….. | 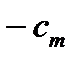
| 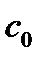
|
Начало алгоритма симплекс-метода.
Шаг 1. По симплекс-таблице находим опорное решение. На первом шаге это будет:
 и
и 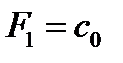 (4)
(4)
Шаг 2. Проверяем условие оптимальности полученного опорного решения. Если последняя (индексная) строка таблицы (3) не содержит отрицательных элементов, то есть, все коэффициенты целевой функции 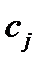 неположительные:
неположительные: 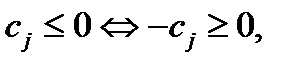 то опорное решение является оптимальным. Решение задачи заканчивается, и мы переходим к шагу 9.
то опорное решение является оптимальным. Решение задачи заканчивается, и мы переходим к шагу 9.
Если условие оптимальности:  , не выполнено, то продолжаем решение задачи.
, не выполнено, то продолжаем решение задачи.
Шаг 3. Выбираем номер 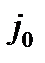 одного из столбцов, содержащих отрицательные элементы в индексной строке. Соответствующий столбец объявляем ведущим.
одного из столбцов, содержащих отрицательные элементы в индексной строке. Соответствующий столбец объявляем ведущим.
Шаг 4. Определяем минимальное допустимое отношение  для каждой строки по правилу:
для каждой строки по правилу:

где 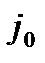 - номер ведущего столбца.
- номер ведущего столбца.
Шаг 5. Выбираем номер 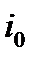 ведущей строки с минимальным допустимым отношением
ведущей строки с минимальным допустимым отношением 
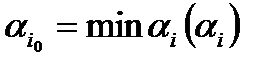 .
.
Соответствующую строку называем ведущей. Если такой выбор невозможен, то есть все 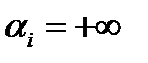 , то заканчиваем решение, поскольку в этом случае задача не имеет решения. Переходим к шагу 10.
, то заканчиваем решение, поскольку в этом случае задача не имеет решения. Переходим к шагу 10.
Шаг 6. Делим ведущую строку на ключевой элемент 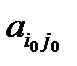 , стоящий на пересечении ведущей строки и ведущего столбца. В результате на месте ключевого элемента
, стоящий на пересечении ведущей строки и ведущего столбца. В результате на месте ключевого элемента  получаем единицу:
получаем единицу: 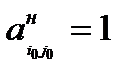 .
.
Шаг 7. Из каждой строки таблицы, кроме ведущей, вычитаем ведущую строку, умноженную на элемент текущей строки, стоящий в ведущем столбце. В результате получаем, что все элементы ведущего столбца, кроме ключевого, равного единице, равны нулю, то есть ведущий столбец превратился в базисный. При этом оказывается, что один из базисных столбцов превратился в свободный (именно, тот, который содержал 1 в ведущей строке). Нами получена новая симплекс-таблица, отличающаяся от прежней набором базисных столбцов.
Шаг 8. Переходим к шагу 1.
Шаг 9. Объявляем, что получено оптимальное решение и выводим результаты решения. Затем переходим на конец алгоритма.
Шаг 10. Сообщаем, что задача не имеет решения и переходим на конец алгоритма.
Конец алгоритма.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 2048; Нарушение авторских прав?; Мы поможем в написании вашей работы!