Графический метод решения задачи ЛП

Рассмотрим графический метод решения однородной двумерной задачи ЛП на конкретном примере.

Пример №1.

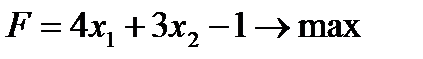
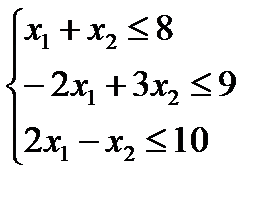
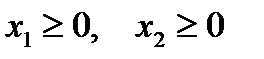
Решение. Найдем вначале область допустимых решений (ОДР). Решим графически первое неравенство:

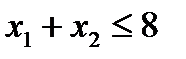(1)

Для этого построим вначале прямую линию, соответствующую уравнению:

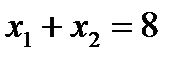. (1¹)

Поскольку, если 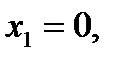то 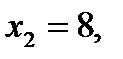то прямая (1¹) проходит через точку М₁ (0;8). Аналогично, если 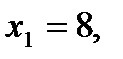то 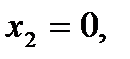и прямая (1¹) проходит также через точку М₂ (8;0). Проведем через эти две точки прямую линию и отметим ее с помощью 1 (см. рис. 1). Эта линия делит плоскость на две полуплоскости, которые мы условно назовем верхней и нижней полуплоскостями. Так как координаты точки (0;0) удовлетворяют неравенству (1), то этому неравенству соответствует нижняя полуплоскость, которая содержит эту точку. Этот факт мы изобразим на рис. 1 штрихами, направленными вниз от линии 1.

Теперь решим графически второе неравенство:

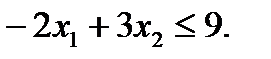(2)

Ему соответствует прямая, заданная уравнением:

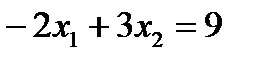(2¹)

Ее мы построим несколько иначе. Перепишем уравнение (2¹) в виде:

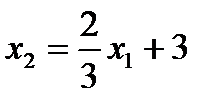
Тогда при 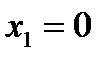оказывается 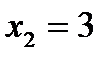, что дает точку М₃ (0;3) искомой прямой. Угловой коэффициент этой прямой 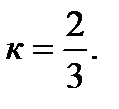Но угловой коэффициент любой прямой равен 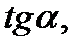где 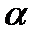- угол наклона прямой к оси 0 х: 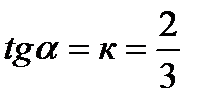. Если теперь мы отложим три единицы вправо от точки М₃ (0;3) и затем две единицы вверх, то получим другую точку М₄ (3;5) которая также лежит на прямой (2¹). Через точки М₃ и М₄ мы проводим прямую 2 (рис.1). Начало координат (0;0) удовлетворяет (2) и лежит ниже графика линии 2, поэтому соответствующая полуплоскость является «нижней», что мы и отмечаем штрихами, направленными вниз от прямой 2 (рис.1). Аналогично строим прямую 3.

Уравнение

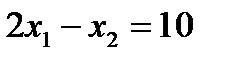(3)

заменяем на уравнение

,

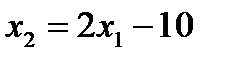Ясно, что прямая проходит через т. М₅ (5;0), и имеет угловой коэффициент к = 2. При этом самому неравенству

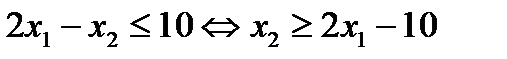
соответствует верхняя полуплоскость, отмеченная штрихами вверх от прямой (3).

Тривиальному неравенству 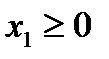соответствует правая полуплоскость координатной плоскости, то есть полуплоскость, лежащая справа от вертикальной оси 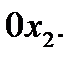Ее отмечаем штрихами, направленными вправо от оси 0 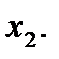Наконец неравенству 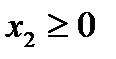соответствует верхняя полуплоскость координатной плоскости, отмеченная штрихами, направленными вверх от оси 0 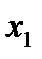. Пересечение всех указанных полуплоскостей определяет ОДР данной задачи. На рисунке 1 это область, ограниченная выпуклым пятиугольником ОАВСD.

Изобразим на рисунке 1 вектор роста 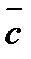целевой функции 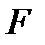. Это вектор 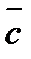началом в т. (0;0) и концом в точке М (4;3), поскольку .

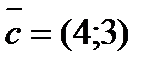Построим теперь линию уровня 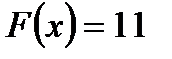. Она определяется уравнением:

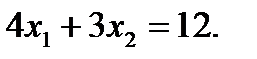(3)

Мы взяли здесь константу С =11, для того чтобы точки пересечения прямой (3) с осями 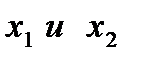имели целые координаты. Действительно, если 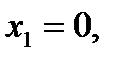то 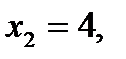и, если 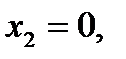то 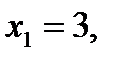что дает две точки М₁ (0;4) и М₂ (3;0) линии уровня (3). Через них проводим пунктиром соответствующую линию уровня (рис. 1). Она оказывается перпендикулярна вектору роста 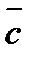. Отрезок 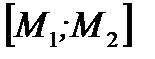пересекается с ОДР и в каждой его точке х значение целевой функции 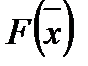равно 11:

.

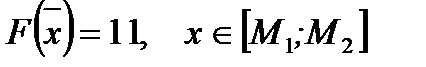Мы знаем, что значение функции F увеличивается в направлении вектора роста 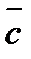. Чтобы найти максимальное значение 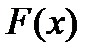на ОДР будем параллельно перемещать линию уровня в направлении вектора роста 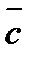до тех пор, пока, она будет иметь хотя бы одну точку пересечения с ОДР задачи. Из рисунка 1 ясно, что последнее пересечение смещенной линии уровня (3) будет точка

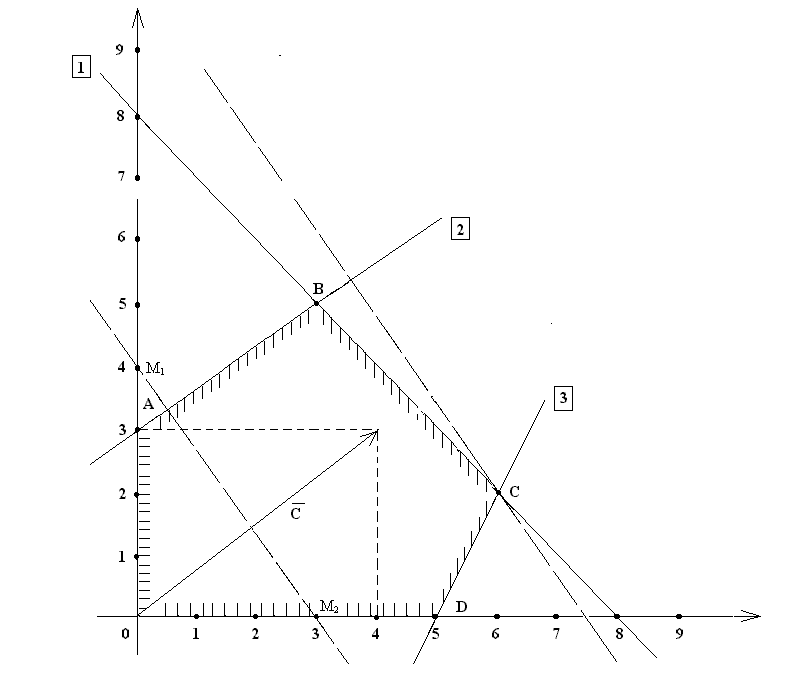Рисунок 1. Графическое решение задачи ЛП.

На этой линии очевидно и будет достигаться максимальное значение целевой функции F в ОДР, поскольку при дальнейшем движении линии уровня в направлении вектора роста, она перестает пересекаться с ОДР. Итак, максимальное значение функция F(х) имеет в точке 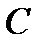. Так как точка 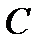является пересечением прямых 1 и 3, то ее координаты находятся из системы:

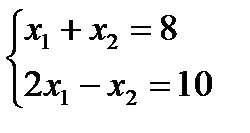(4)

Чтобы решить эту систему, сложим оба уровня. Тогда получим, что 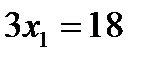или .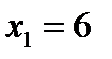

Из первого уравнения находим, что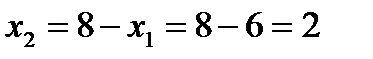

Итак, координаты точки С найдены – С (6;2). Найдем максимальное значение функции:

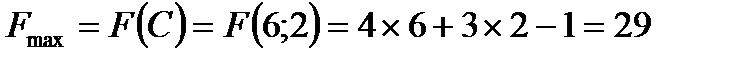
Задача решена

Ответ: максимальное значение целевой функции F достигается в точке С (6;2) и равно 29:

.

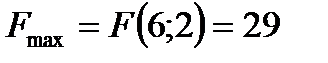1.6. Выпуклые множества на плоскости и в пространстве.

Определение 1. Множество А 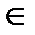Rⁿ называется выпуклым, если с любыми своими двумя точками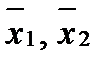 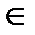А оно содержит целиком отрезок 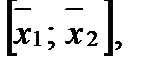их соединяющий:

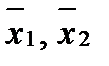
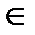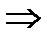
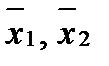
А 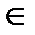А. (1)

Пусть 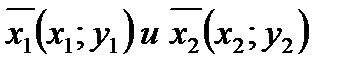два вектора на плоскости х О у и пусть точка 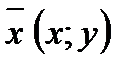лежит на отрезке . Тогда вектор 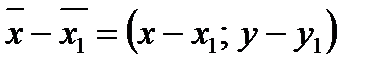колинеарен вектору , направлен в одну сторону с ним и не превосходит его по длине. Эти условия могут быть записаны в виде равенства:

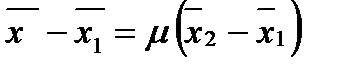, (2)

где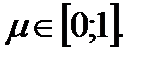

Векторное равенство (2) равносильно системе:

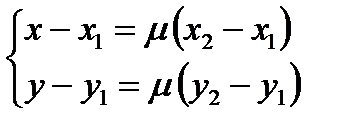(3)

Система (3) может быть преобразована в равносильную систему:

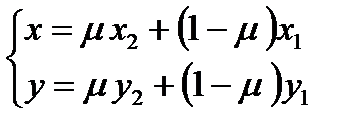(4)

где Обозначим 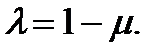Тогда (4) примет вид:

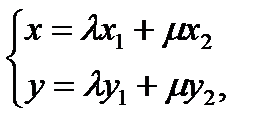(5)

где

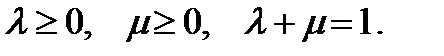
В векторном виде система (5) примет вид:

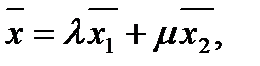
где 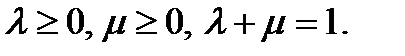(6)

Определение 2. Выпуклой (линейной) комбинацией векторов называется выражение вида:

где все 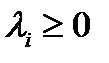и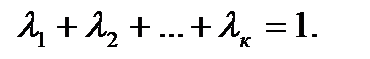

Равенство (6) показывает, что каждая точка 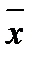отрезка 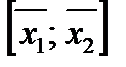является выпуклой комбинацией векторов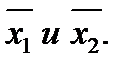

Теорема 1. Пересечение любого числа выпуклых множеств является выпуклым множеством.

Доказательство. Пусть 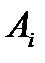- любое семейство выпуклых множеств. Пусть А – их пересечение: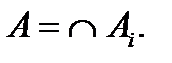

Покажем, что множество А – выпукло. Пусть 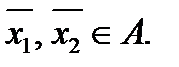Тогда 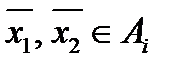для каждого 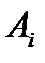, поскольку А – пересечение всех 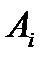. Так как 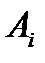- выпукло, то вместе с точками 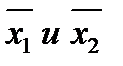оно содержит и соединяющий их отрезок:

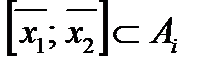для всех А_i.

Но, отсюда, очевидно, следует, что каждая точка отрезка 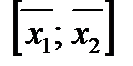(а значит и сам отрезок) принадлежит пересечению множеств 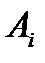, то есть множеству А. Итак, А – выпуклое множество. Что и требовалось доказать.

Определение 3. Выпуклой оболочкой множества 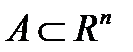называется такое выпуклое множество 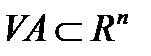, что:

1) ,

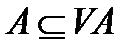2) 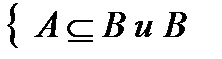- выпукло .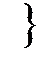

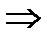
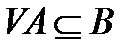Лемма 1. Выпуклая оболочка множества А совпадает с пересечением всех выпуклых множеств, содержащих А.

Доказательство. Пусть В₀ – пересечение всех выпуклых множеств, содержащих А. Тогда очевидно В₀, содержит А. С другой стороны по теореме 1 множество В₀ само выпукло. Отсюда следует, что В₀= VA, поскольку выполнены свойства 1) и 2).

Лемма 2. Отрезок 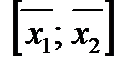является выпуклой оболочкой своих концов .

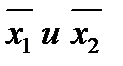Доказательство. Пусть 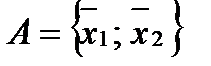, то есть множество А состоит из двух элементов 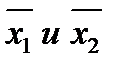. Отрезок 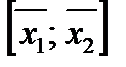является выпуклым множеством и содержит А. С другой стороны каждое выпуклое множество В, содержащее А, содержит по определению выпуклости и весь отрезок 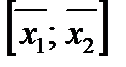. Тем самым показано, что 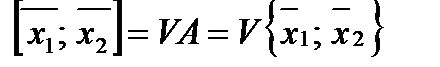ч т.д.

Лемма 3. Если выпуклое множество 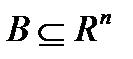содержит векторы 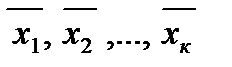, то оно содержит и любую их выпуклую комбинацию:

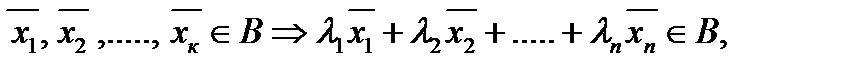
где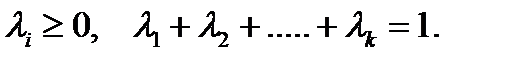

Доказательство. Докажем это по индукции. Для двух точек 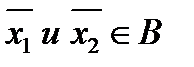утверждение леммы практически было доказано выше, поскольку множество выпуклых комбинаций 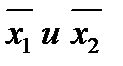совпадает с отрезком 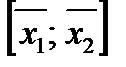и, следовательно, содержится в В. Пусть утверждение справедливо для всех 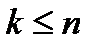. Покажем, что оно будет также справедливым и для .

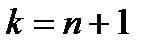Пусть 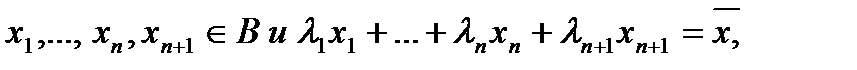где

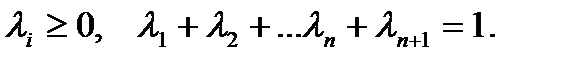
Пусть

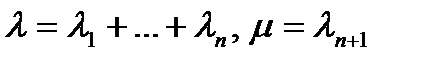
и .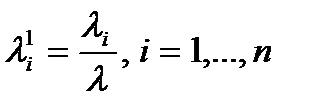

Тогда

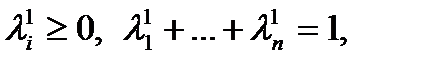
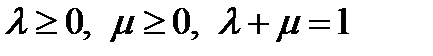
и

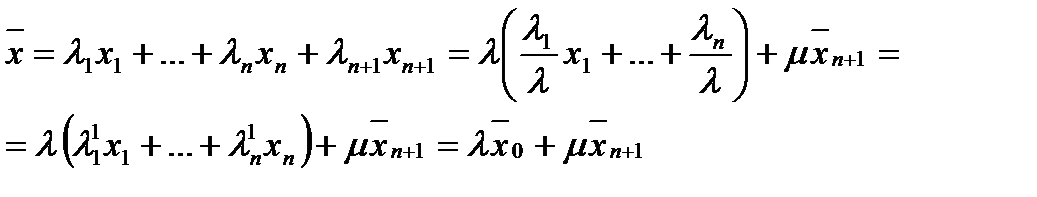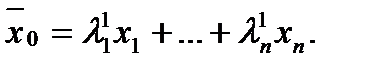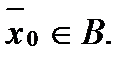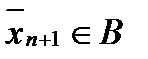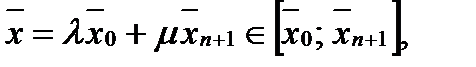где По предположению индукции Так как и то 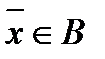. Лемма доказана.

Теорема 2. Выпуклая оболочка VA множества А 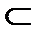Rⁿ совпадает с множеством всех выпуклых комбинаций, состоящих из конечного числа векторов множества А.

Доказательство: Пусть В₀ – множество всех таких комбинаций векторов множества А. Как следует из леммы 3 множество В₀ содержится в любом выпуклом множестве В, содержащем А. Осталось показать, что само В₀ – выпукло.

Пусть 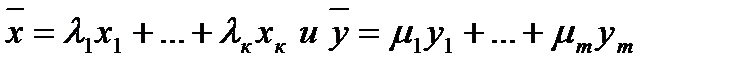- два вектора множества В₀. Тогда , , , .

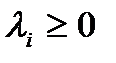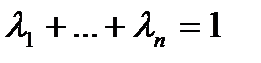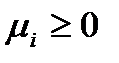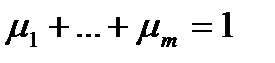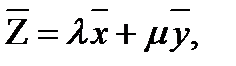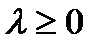Пусть - где и 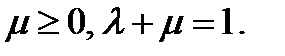Достаточно показать, что 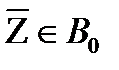, то есть что вектор 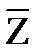сам является выпуклой комбинацией векторов из А_0. Но это верно, поскольку:

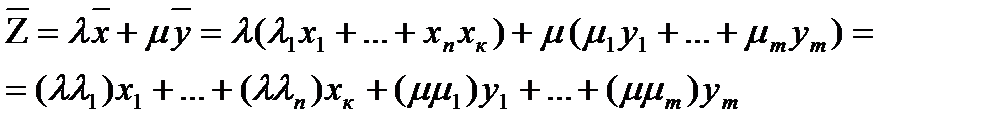
- выпуклая комбинация векторов 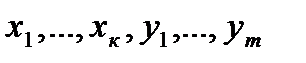- так как 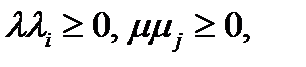и 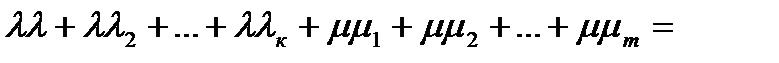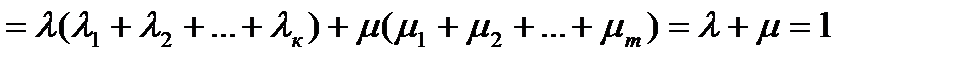ч.т.д.

Отметим, что треугольник и пирамида являются выпуклыми оболочками своих вершин, и, следовательно, каждая их точка является выпуклой комбинацией векторов-вершин.

Определение. Выпуклая оболочка 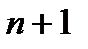точки в 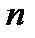- мерном линейном пространстве 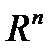называется симплексом.

Предполагается, что точки лежат в общем положении, то есть не содержатся ни в какой гиперплоскости.

Рассмотрим некоторую точку 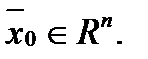Возможны следующие случаи расположения точки 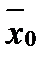относительно множества В.

Первый случай. На каждой прямой l, проходящей через 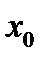, можно найти отрезок 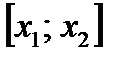, лежащий целиком в В и содержащий 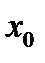внутри себя:

1)

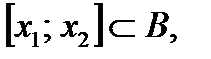
2) 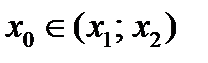. (7)

Второй случай. Существует содержащая 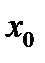прямая 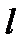, на которой не существует отрезка 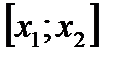, удовлетворяющего (7).

Если 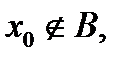то ясно, что свойством (7) не обладает ни один отрезок 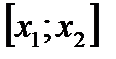. Если для некоторых прямых проходящих через точку 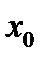отрезок удовлетворяющий (7), существует, а для других прямых нет, то 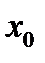называется граничной точкой множества В. Вблизи граничной точки 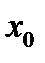лежат как точки множества В, так и точки ему не принадлежащие.

Третий случай.

Определение. Пусть точка 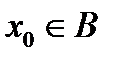и ни для одной прямой l содержащей 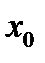, не существует отрезка 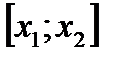, удовлетворяющего (7). В этом случае 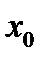называется угловой точкой множества В.

Другими словами любой отрезок, содержащий угловую точку 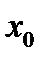внутри себя, обязательно «высовывается» из множества В.

Замечание.

Условие 2) Из (7) можно заменить в предыдущих рассуждениях на условие: 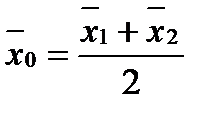, - то есть можно считать, без ограничения общности, что точка 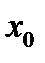является серединой отрезка 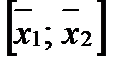, действительно, если существует отрезок, содержащий 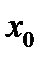внутри себя, то существует в нем меньший отрезок, для которого точка 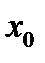является серединой.

Определение. Множество 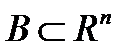называется замкнутым, если оно содержит все свои граничные точки.

Значение угловых точек для описания выпуклого множества в 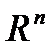дает следующая теорема, которую мы приводим без доказательства.

Теорема 3. Замкнутое выпуклое множество 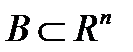является выпуклой оболочкой своих угловых точек.

1.7. Геометрическая интерпретация однородной задачи линейного программирования.

Рассмотрим вначале однородную задачу линейного программирования на плоскости.

Каждому ограничению вида неравенства:

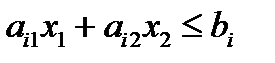, (1)

- соответствует замкнутая полуплоскость 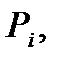границей, которой является прямая линия 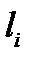, определяемая соответствующим уравнением:

. (2)

Системе ограничений однородной задачи:

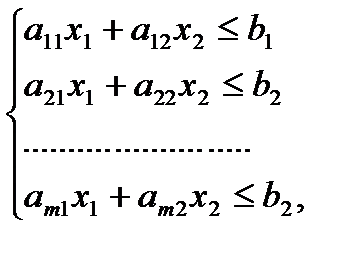(3)

- соответствует пересечение полуплоскостей Тривиальным ограничениям:

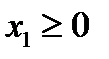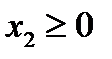и , (4)

- также соответствуют полуплоскост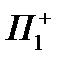и и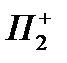

При этом 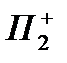называют, обычно, верхней (координатной) полуплоскостью, а 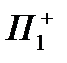- правой (координатной) полуплоскостью.

Таким образом, ОДР однородной задачи ЛП на плоскости представляет из себя пересечение конечного числа замкнутых полуплоскостей.

Очевидно, каждая полуплоскость является выпуклым множеством. По теореме 1 п. 1.5. их пересечение также выпукло.

Определение 1. Область, которая являеться пересечением конечного числа замкнутых полуплоскостей называется замкнутой выпуклой многоугольной областью.

Если замкнутая выпуклая многоугольная область ограничена, то она называется замкнутым выпуклым многоугольником.

В примере №1 п.1.4. это замкнутый выпуклый пятиугольник ОАВСД.

Целевой функции.

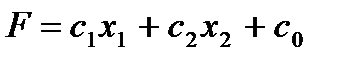(5)

соответствует вектор роста 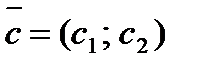и линии уровня

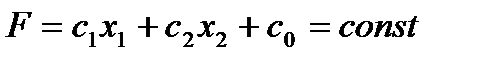(6)

На рисунке 1. п 1.4. это линии (А) и (В).

При этом значение функции 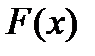растет в направлении вектора роста 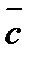, перпендикулярного линиям уровня.

Таким образом, геометрически однородная задача ЛП на плоскости может быть сформулирована следующим образом: найти крайнюю (угловую) точку, в которой линия уровня все еще пересекает замкнутую выпуклую многоугольную область при параллельном переносе этой линии в направлении вектора роста (или в противоположном направлении).

В трехмерном пространстве R³ каждому линейному неравенству

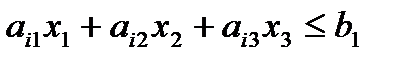(7)

Соответствует одно из замкнутых полупространств, на которые делит все пространство R³ плоскость p_i, определенная уравнением:

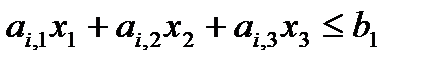(8)

Соответственно вектор роста 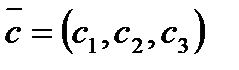перпендикулярен каждой поверхности уровня целевой функции, задаваемой уравнением:

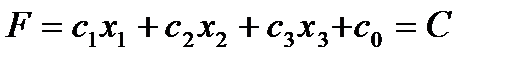, (9)

где С – некая произвольная константа.

Определение 2. Область, которая являеться пересечением конечного числа замкнутых полупространств в R³ называется выпуклой многогранной областью. Ограниченная выпуклая многогранная область называется выпуклым многогранником.

Однородная задача ЛП в пространстве R³ может быть сформулирована так: найти крайнюю (угловую) точку, в которой поверхность уровня при движении в направлении вектора роста (или в противоположном направлении) все еще пересекает заданную выпуклую многогранную область.

Заметим, что при этом поверхность уровня представляет из себя плоскость, определяемую уравнением (9). Вектор роста 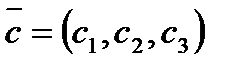является вектором нормали этой плоскости.

Соответствующая формулировка в n – мерном пространстве Rⁿ фактически совпадает с данной. Единственное отличие состоит в том, что уравнение поверхности уровня:

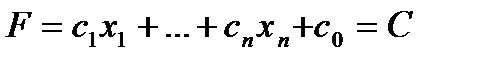(10)

задает не плоскость, а гиперплоскость в Rⁿ.

Дата добавления: 2014-12-26