Примеры задач линейного программирования

Пример 1. Пусть малое предприятие «Стакан» продает два вида прохладительных напитков, скажем, «Колокольчик» и «Буратино». Оба напитка изготавливаются тут же на месте из имеющихся запасов газированной воды, фруктового сиропа, лимонной кислоты и льда. Нормы расхода сырья на одну порцию готовой продукции и его запасы приведем для удобства в виде таблицы.

Виды сырья	Нормы расхода сырья на 1 порцию продукции	Запасы сырья на одни сутки
Колокольчик	Буратино
Газированная вода	0,450 л.	0,48 л.	900 л.
Фруктовый сироп	0,050 л.	0,020 л.	80 л.
Лимонная кислота	0,001 л.	0,002 л.	12 л.
Лед в кубиках по 10 г.	20 г.	30 г.	20 кг.

Допустим, что одна проданная порция «Колокольчика» приносит предприятию 5 рублей прибыли, порция «Буратино» - 6 рублей. Также предположим, что нет никаких проблем с изготовлением необходимого количества порций напитков и, что спрос перекрывает предложение.

Возникает вполне естественный вопрос - сколько порций того и другого напитка следует произвести из имеющегося сырья, чтобы получить максимальную прибыль?

Составим математическую модель данной задачи.

Во-первых, введем переменные. Пусть 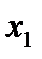- количество порций «Колокольчика», которое следует произвести, а 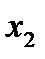- количество порций «Буратино».

Во-вторых, введем оптимизируемую целевую функцию, в данном случае прибыль: F .

Тот факт, что следует найти максимум, функции запишем следующим образом:

F 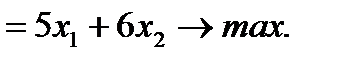(1)

В-третьих, запишем имеющиеся (нетривиальные) ограничения по сырью, вытекающие из того, что объем израсходованного на производство напитков сырья не превышает его суточного запаса.

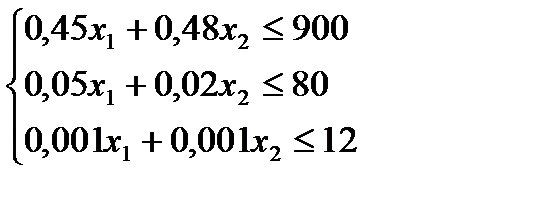(2)

Добавим сюда тривиальные (очевидные) ограничения:

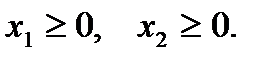(3)

Условие (1) вместе с ограничениями (2), (3) и дают требуемую математическую модель, которая является частным случаем задачи линейного программирования (см. п. 1.2.).

Как мы увидим позже, модель примера №1 является однородной задачей линейного программирования (см. п. 1.3.).

Дадим обобщение примера №1.

Пример 2. Пусть предприятие выпускает к- типов продукции, используя т- видов ресурсов. При этом расход i -го вида ресурса на единицу j -го вида продукции составляют 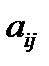; всего имеется объем 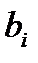запаса i- го вида ресурса; реализация единицы продукции j -го вида дает 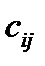условных денежных единиц прибыли. Требуется составить оптимальный план выпуска продукции.

Модель задачи имеет в этом случае вид:

F

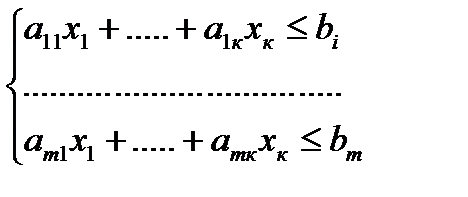
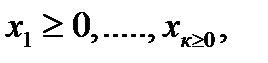
где 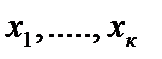- объемы планируемого выпуска продукции.

Дата добавления: 2014-12-26