Без искажения

Проекций, то на эту плоскость проекций прямой угол проецируется

Если одна из сторон прямого угла параллельна какой-либо плоскости

Перпендикулярность

Из рассмотрения задачи о нахождении натуральной величины отрезка прямой уровня следует вывод о том, что плоская фигура или угол (а он образуется двумя сторонами фигуры) на плоскость проецируется без искажения, если плоскость фигуры и плоскость проекции - параллельны. Исключение составля­ет прямой угол.

Формулировка теоремы о частном случае проецирования прямого уг­ла звучит так:

А. Перпендикулярность двух прямых,

Решим следующую задачу:

Через точку М провести прямую, перпендикулярную отрезку АВ. Сколько возможно решений, и какие они могут быть (рис. 35)?

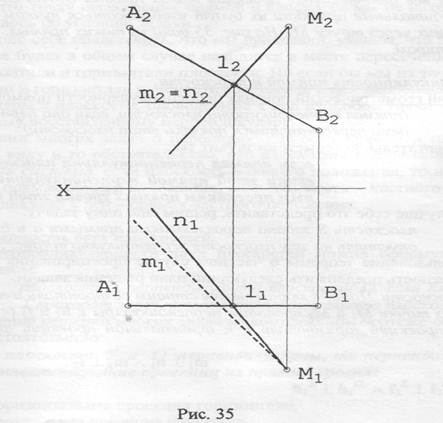
Обратим внимание на прямую АВ. Это - фронталь. На основании только что сформулированной теоремы на фронтальной плоскости проекций можно из точки М₂ провести прямую n₂, перпендикулярную А₂В₂:

n 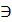М ^ n ┴АВ => n₂ 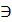М₂ ^ n₂ ┴А₂В₂.

Могут существовать два варианта решения, в зависимости от того, как расположены прямые n и АВ по отношению друг к другу.

1. Если п и АВ пересекаются, l₂ — фронтальная проекция их точки пересечения 1. Горизонтальная проекция 1₁ точки 1 может быть найдена по принадлежности к прямой АВ и тем самым определится единственное положение прямой п (другими словами, задача имеет единственное ре­шение):

1 = n 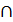АВ => 1₂ = п₂ 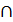А₂В₂ => 1₁ = 1₁1₂ 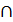А₁В₁ => n₁ = М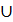₁ l₁

2. Если п и АВ - не пересекаются, то есть п и АВ - скрещивающиеся прямые, тогда прямые п и АВ общих точек не имеют. Все прямые, скрещивающиеся с АВ под прямым углом, будут располагаться в плоскости, проходящей через точку М и перпендикулярной к отрезку АВ. Посколь­ку через точку в плоскости можно провести бесконечное множество прямых, решений будет бесконечное множество. На комплексном чер­теже все фронтальные проекции таких прямых будут совпадать с п₂, горизонтальные проекции их будут изображаться пучком прямых, про­ходящих через точку М₁. На рис. 35 одна из таких прямых, m₁, показана пунктиром.

Б. Перпендикулярность прямой и плоскости.

Общий геометрический признак перпендикулярности прямой и плоскости (прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости) в начертательной геометрии звучит так:

если прямая перпендикулярна плоскости, то про­екции этой прямой перпендикулярны одноимен­ным проекциям прямых уровня этой плоскости.

Чтобы лучше себе это представить, решим еще одну задачу:

плоскость S задана параллельными прямыми а и b. Из точки М опустить на эту плоскость перпендикуляр т (рис. 36).

Использование теоремы о частном случае проецирования прямого угла даёт возможность предложить следующий план решения задачи:

1. В плоскости Σ(а//b) в любом месте строим её фронталь и горизонталь;

2. Через точки М₁ и M₂проводим перпендикуляры к h₁ и f₂ (к горизонталь­
ной проекции горизонтали и к фронтальной проекции фронтали), то
есть: m₁ ┴ h₁ ^ m₂ ┴ f₂.

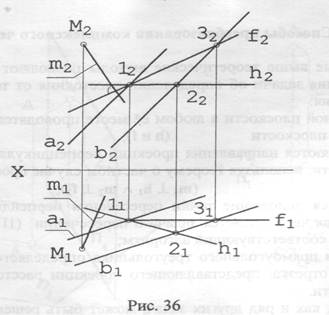
Заметим, что точку пересечения прямой и плоскости мы не находили, да это и не требовалось по условию задачи.

Чтобы лучше себе представить, что мы проделали, уясним, что эта точка пересечения и не будет в общем случае находится в месте пересечения проведенной нами фронтали и горизонтали плоскости. Но если бы мы из точки пере­сечения фронтали и горизонтали плоскости восставили к ней перпендикуляр, то все перпендикуляры к плоскости, проведенные к ней из любой точки, были бы параллельны этому восставленному перпендикуляру.

При решении многих задач о перпендикулярности прямой и плоскости следует иметь в виду и то обстоятельство, что плоскость и перпендикуляр к ней - «жёсткая» система: если плоскость - общего положения, то и перпендикуляр к ней - прямая общего положения; если плоскость - частного положе­ния, то и перпендикуляр к ней - прямая частного положения.

В. Перпендикулярность двух плоскостей.

Признак перпендикулярности двух плоскостей можно сформулировать следующим образом:

плоскость Σ перпендикулярна плоскости Ω если плоскость Σ проходит через прямую, перпендикулярную плоскости Ω.

Представление решений многих задач на комплексном чертеже облегчает и следующее обстоятельство:

если плоскости Σ и Ω перпендикулярны, то перпендикулярны и соответствующие проекции их прямых уровня: h₁^Σ ┴ h₁^Ω ^ f₂^Σ ┴ f₂^Ω

где h₁ – горизонтальная проекция горизонтали;

f₂ - фронтальная проекция фронтали,

а Σ и Ω определяют принадлежность их к той или иной плоскости.

Дата добавления: 2014-12-27