
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Главные позиционные задачи
|
|
|
|
Как в геометрической, так и в конструкторской практике большое число решений относится к задачам о пересечении геометрических образов или геометрических тел. Ввиду их особой важности, задачи о пересечениях называют главными позиционными задачами (ГПЗ).
Из всего разнообразия возможных при этом вариантов можно выделить две разновидности ГПЗ:
- 1ГПЗ: пересечение линий и поверхностей;
- 2ГПЗ: пересечение поверхностей.
Очевидно, что сказанное о двух ГПЗ характеризует самый общий вариант для каждой из задач и подразумевает, что понятие каждого из компонентов пересечения (линия, поверхность) включает в себя все возможные его варианты. Так, к 1 ГПЗ относятся пересечения:
- прямой линии и плоскости;
- прямой линии и поверхности;
- кривой линии и плоскости;
- кривой линии и поверхности (в общем случае).
Ко 2-й ГПЗ относятся пересечения:
- плоскостей;
- плоскости и поверхности;
- поверхностей.
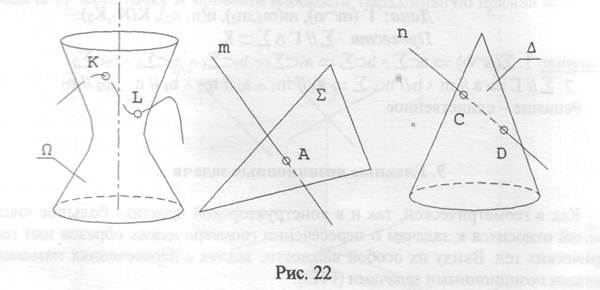
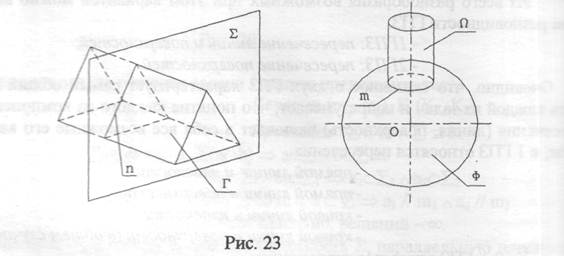
Сущность всякой задачи на пересечение состоит в определении общего элемента, который будем называть искомым геометрическим образом. Очевидно, в 1-й ГПЗ это - точка или несколько (конечное число) точек (рис.22). Во 2-й ГПЗ искомым геометрическим образом является линия (рис.23).
Искомый геометрический образ как результат пересечения заданных образов всегда принадлежит одновременно обоим заданным пересекающимся геометрическим образам и, очевидно, может быть определен:
- непосредственно, исходя из свойств пересекающихся образов;
- через посредство свойств нового геометрического образа
или их совокупность.
|
|
Направление методики решения предполагает использование проецирующих свойств геометрических образов. Поскольку геометрические образы могут быть как проецирующие, так и не проецирующие, очевидно, что как для 1 ГПЗ, так и для 2 ГПЗ при всем многообразии вариантов возможно существование трех случаев пересечения:
Случай 1. Оба пересекающихся геометрических образа проецирующего
характера;
Случай 2. Один из пересекающихся геометрических образов проецирующего характера, а второй — не проецирующий;
Случай 3. Оба пересекающихся геометрических образа - непроецирующего характера.
Имея в виду то определение главной проекции геометрического образа, которое было дано ранее, очевидно, можно утверждать, что
в случае 1 непосредственно на чертеже можно указать
обе проекции искомого геометрического образа;
в случае 2 непосредственно на чертеже можно определить
одну проекцию искомого геометрического образа;
В случае 3 определение проекций искомого геометрического образа потребует введения нового геометрического образа-посредника, обладающего свойствами проецирующих образов.
Эти соображения вытекают из того, что точка, линия, фигура, принадлежащ ая проецирующему геометрическому образу, будет иметь свои одноименные проекции, совпадающие с главной проекцией этого образа.
Все высказанное позволяет не только систематизировать все возможные случаи пересечения, но и алгоритмизировать сам процесс решения задач для все трех случаев.
Самое главное из всего вышеизложенного о главных позиционных задачах (ГПЗ) можно объединить в двух таблицах, полезных для использования при решении задач о пересечении геометрических образов.


Чтобы увидеть общее в решении задач на пересечение и выяснить алгоритм для того или иного случая пересечения, рассмотрим решения ряда задач.
Задача 1. Даны прямая m(m1,m2) и плоскость Σ(n//k).
Требуется определить точку А пересечения прямой m и плоскости Σ(n//k).
Решение(рис.24):
1. А 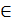 m => А2
m => А2 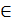 m2
m2 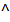 А]
А] 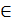 m]
m]
2. А 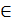 Σ => А2
Σ => А2 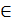 Σ2 (k2 ≡ n2)
Σ2 (k2 ≡ n2) 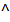 А1
А1 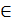 Σ1(n1//k1).
Σ1(n1//k1).
1. m1 ╨ П1 => m1 ≡ A1
2. Σ ╨ П2 =>Σ2 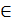 А2
А2 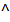 А2 = m2
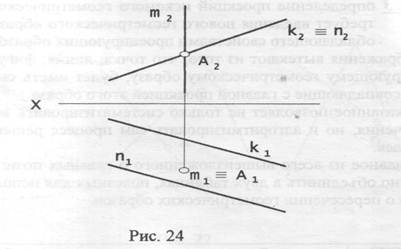
А2 = m2 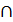 k2 = n2 (рис. 25)
k2 = n2 (рис. 25)
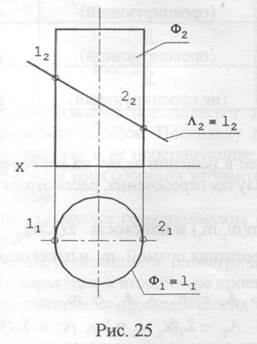
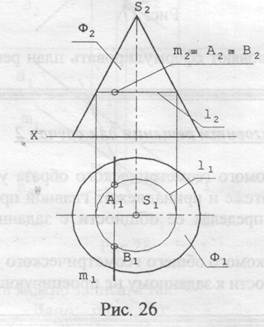
Задача 2. Заданы плоскость ˄ (˄2) и цилиндрическая поверхность Ф(Ф1, Ф2,) Определить линию пересечения l плоскости ˄ с поверхностью Ф.
Решение (рис. 25):
1.l 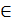 ˄ => l2
˄ => l2 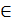 ˄2
˄2 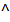 l]
l] 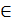 ˄]
˄]
2. l 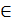 Ф => l1
Ф => l1 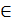 Ф1
Ф1 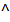 l2
l2 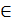 Ф2
Ф2
3. ˄ ╨ П2 => l2 ≡ ˄2(l2 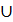 22)
22)
4. Ф ╨ П1 => Ф1 ≡ l1
|
Замечание. При рассмотрении интервала существования l необходимо помнить, что общность искомого геометрического образа определяет граница его существования в пределах общей принадлежности к заданным геометрическим образам (здесь эта граница определена точками 1 и 2).
Мы рассмотрели в задаче 1-1 ГПЗ, а в задаче 2-2 ГПЗ. Если сравнить их решения, можно заметить, что, во-первых, мы рассмотрели задачи, попадающие под первый случай пересечения, во-вторых, решение задач, в общем, не отличаются друг от друга. Значит, существует единый, общий для 1ГПЗ и для 2ГПЗ алгоритм решения, который мы сейчас и сформулируем.
Алгоритм решения для случая 1
1. Обе проекции искомого общего геометрического образа уже непосредственно заданы на чертеже.
2. Обе проекции искомого общего геометрического образа принадлежат главным проекциям проецирующих образов в пределах общности этих проекций.
3. Решение задачи может быть сведено к простановке обозначений проекций искомого общего геометрического образа на чертеже.

|

|
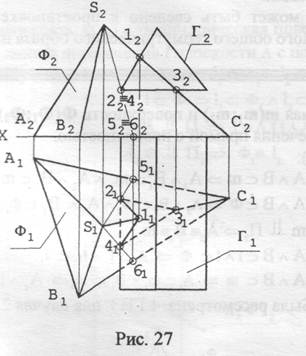
Примеры 3 и 4 позволяют сформулировать план решения задач для второго случая пересечения.
Алгоритм решения для случая 2
1. Одна проекция искомого геометрического образа уже непосредственно задана на чертеже и принадлежит главной проекции проецирующего образа в пределах её общности с заданным не проецирующим образом.
2. Другая проекция искомого общего геометрического образа определяется по принадлежности к заданному не проецирующему образу.
Задача 5.Заданы прямая m общего положения и плоскость общего положения Σ в виде двух пересекающихся прямых а и в. Определить точку М пересечения прямой m и плоскости Σ (рис. 28). Прежде, чем записать решение этой и следующей задачи, попробуем предложить следующий план решения.
Алгоритм решения 1ГПЗ для случая 3
1. Через заданную прямую проводится плоскость-посредник; целесообразно, чтобы эта плоскость была проецирующего характера.
2. Строится линия пересечения заданной плоскости и плоскости-посредника (второй случай пересечения!).
3. Определяется точка пересечения заданной прямой и построенной линии пересечения, которая и будет искомой точкой.
Эти же соображения можно сформулировать и в том случае, когда надо найти линию пересечения, а в качестве посредников выбраны некоторые поверхности. Сама же искомая линия будет представлена совокупностью точек.
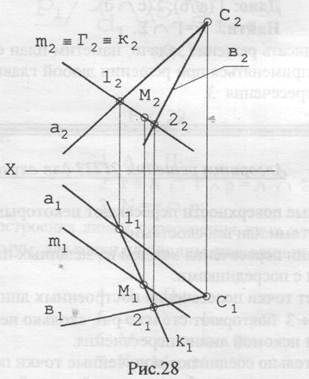
Данные этой задачи можно записать так:
Дано: m(m1, m2);
Σ(a 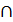 b)= Σ1(a1
b)= Σ1(a1 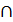 b1)
b1) 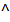 Σ2(a2
Σ2(a2 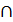 b2)
b2)

Для задач на третий случай пересечения условимся записывать только решение в пространстве, что в более краткой форме отражает как суть производимых построений, так и применяемый алгоритм решения:
1. Г 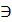 m ^ Г ╨ П2;
m ^ Г ╨ П2;
2. k=Г 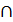 Σ(а
Σ(а 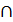 b);
b);
3. М = m 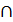 k.
k.
Следует отметить, что посредник мог быть другим, однако в данном случае проецирующее свойство посредника позволило использовать алгоритм для второго случая пересечения, что упростило задачу.
Рассмотрим еще один пример.
Задача 6. Даны две плоскости общего положения: плоскость Г задана параллельными прямыми а иb, плоскость Σ - пересекающимися прямыми с и d. Найти линию k пересечения этих плоскостей.
Кратко условие этой задачи можно записать так:
Дано: Г(а//b); Σ(c 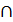 d). Найти: к=Г
d). Найти: к=Г 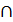 Σ.
Σ.
Прежде чем записать решение задачи, наметим план её решения, который в дальнейшем будет применяться при решении любой главной позиционной задачи 2 для случая пересечения 3.
Алгоритм решения 2ГПЗ для случая 3
1. Обе заданные поверхности пересекают некоторыми посредниками
(поверхностями или плоскостями).
2. Строят линии пересечения каждой из заданных плоскостей или поверхностей с посредниками.
3. Определяют точки пересечения построенных линий пересечения.
4. Пункты 1-3 повторяют столько раз, сколько необходимо точек для
построения искомой линии пересечения.
5. Последовательно соединяют полученные точки пересечения в некоторую линию, которая и будет искомой линией пересечения.
В этом варианте решение может быть записано так (рис. 29):
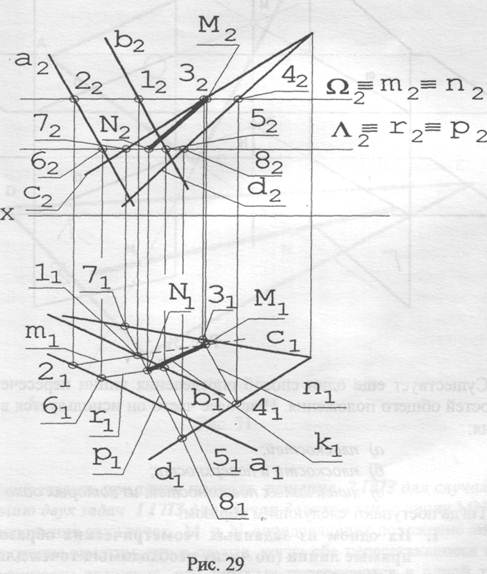
Решение:
1. ˄ ╨П2;
2. r = ˄ 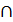 Г ^ p = ˄
Г ^ p = ˄ 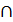 Σ;
Σ;
3. N = r 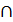 p;
p;
Так как для построения линии пересечения двух плоскостей - прямой - надо знать, как минимум, две точки, проводим еще один посредник (О.). Тогда:
4. Ω ╨П2;
5. m=Ω 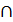 Г ^ n = Ω
Г ^ n = Ω 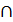 Σ;
Σ;
6. М = m 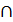 n;
n;
7. К = M  N.
N.
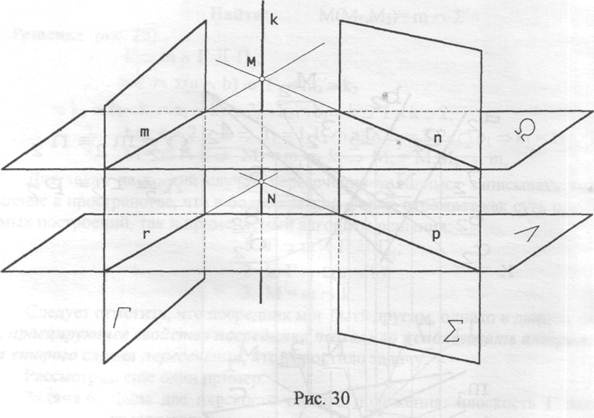
То, что мы здесь проделали, можно проиллюстрировать рис. 30.
Заметим, что задача построения каждой из линий r, р, m и n - задача на второй случай пересечения, то есть, решение 2 ГПЗ для случая пересечения 3 к решению четырёх задач на второй случай пересечения!
Существует еще один способ определения линии пересечения двух поверхностей общего положения. Наиболее часто он используется в случае пересечения:
а) плоскостей;
б) плоскости и поверхности;
в) линейчатых поверхностей, из которых одна - гранная.
Тогда поступают следующим образом:
1. На одном из заданных геометрических образов выделяют
прямые линии (по числу необходимых точек для построения
линии пересечения).
2. Определяют точки пересечения выделенных прямых с другим заданным геометрическим образом.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 4028; Нарушение авторских прав?; Мы поможем в написании вашей работы!