Способ замены плоскостей проекций

Способы преобразования комплексного чертежа

Изложенные выше теоретические выводы позволяют наметить следующий план решения задачи об определении расстояния от точки до плоскости общего положения:

1) в заданной плоскости в любом её месте проводятся фронталь и горизонталь плоскости (h и f);

2) определяются направления проекций перпендикуляра m к заданной плоскости, используя теорему о частном случае проецирования прямо­го угла (m₁ ┴ h₁ ^m₂ ┴ f₂.);

3) находится положение точки пересечения перпендикуляра с плоскоcтью, для чего решается задача о пересечении (1ГПЗ, случай 3), ис­пользуя соответствующий алгоритм;

4) методом прямоугольного треугольника определяется натуральная величина отрезка, представляющего проекции расстояния от точки до плоскости.

Эта задача, как и ряд других задач, может быть решена проще, если каким-либо образом преобразовать комплексный чертёж так, чтобы хотя бы один из заданных геометрических образов стал образом частного положения.

В ряде случаев графическое решение задач может быть упрощено, если заданные плоскости проекций заменить на новые, такие, что в результате по­добной замены геометрические объекты займут частное положение.

Сущность способа замены плоскостей проекций заключается в том, что заданные плоскости последовательно заменяются на новые при неизменном положении геометрических объектов в пространстве. Каждая новая плоскость проекций располагается перпендикулярно к незаменяемой плоскости проек­ций.

Следует подчеркнуть, что сразу обе заданные плоскости проекций заме­нить нельзя. Если возникает необходимость замены двух плоскостей проекций, нужно заменить сначала одну плоскость проекций, а затем - другую, то есть необходимо сделать два преобразования.

Отметим, что при введении новой фронтальной плоскости проекций координаты Z всех геометрических объектов остаются неизменными как в ис­ходной системе плоскостей проекций, так и в новой; при введении новой гори­зонтальной плоскости проекций неизменными и в исходной, и в новой системе плоскостей проекций остаются координаты У.

Рассмотрим эти положения на примере с точкой (рис. 37).

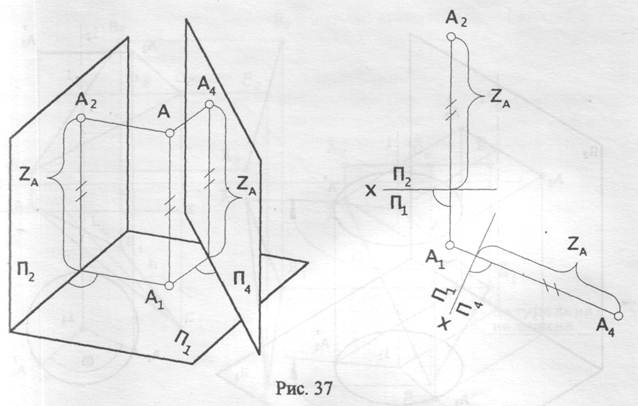
На рисунке и на чертеже здесь показаны те преобразования, которые должны быть выполнены при введении (замене) новой плоскости проекций П₄.

Дата добавления: 2014-12-27